SCI论文(www.lunwensci.com)
摘要:初中阶段,动点问题属于一种比较复杂的变换问题,涵盖了圆、三角形、直角坐标系等知识点,很多学生很难把握动点问题中的变量与不变量,因而不能有效地解决动点问题.教师应从动点问题的本质出发,依据学生的知识情况和思维能力,引导学生掌握正确的解题方法,发展学生的思维能力,有效提高学生综合运用数学知识解决动点问题的能力.
关键词:动点问题;解题指导;教学策略
初中数学动点问题一直都是数学教学重点,也是学生不易解答的难点.动点问题不仅具有综合性和复杂性,还蕴含了化归、数形结合、分类讨论等数学思想,需要学生有较高的信息处理能力和知识综合应用能力.因此,教师要结合动点问题的特点和本质,引导学生对其进行分析和探讨,渗透相应的数学思想方法,锻炼学生的思维,引导学生以动态的、综合的视角去分析和解决动点问题,提高学生的解题能力.
1联系生活,有效解决问题
新课程下,有些题目不但考查学生的基础知识和运算能力,而且将数学问题融合到实际的生活情境中,要求学生能够从中提取出有效的信息,并对其进行分析,形成数学问题或模型,然后运用所学理论解决实际问题,提高数学知识的应用能力,实现学以致用的目的[1].在生活中,常常存在一些运动现象,学生要能结合具体的情境,对生活现象进行抽象和概括,并将其转化为动点问题,这样才能利用已有的数学知识分析和解决问题[2].
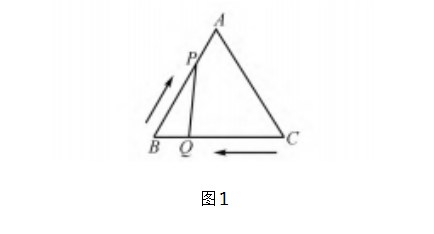
例1 A、B、C三地之间的距离相等,都为60 km,三地连线构成一个等边三角形,已知自行车的速度为20 km/h,电动车的速度为30 km/h,已知P骑自行车,Q骑电动车,在某一时刻,P、Q二人同时出发,P从B地出发向A地运动,Q从C地出发向B地运动,那么,在P、Q二人到达目的地前:
(1)是否会形成等边三角形PQB,如果会,请计算出P、Q二人出发后经过的时间,如果不会,请说明理由.
(2)若某一时刻,P、Q二人与B地组成的三角形PQB为直角三角形,求P、Q运动的时间.
分析题目以运动为背景,考查学生的信息提取能力和知识综合应用能力,依据题目信息,可以将P、Q二人运动的方向在图中画出来,如图1所示,当三角形PQB为等边三角形的时候,需要满足PB=BQ=QP,这样通过题中的数据计算即可.而当三角形PQB为直角三角形的时候,分为∠BPQ和∠BQP为直角两种情况,学生需要分类讨论,这样才能够全面的解答问题.
2动中寻静,找到解题关键
动点问题的难点在于某一个或几个点处于运动状态,动点在不同位置会出现不同的图形,以此增加了问题的难度,使问题复杂化,学生不易从中找出解题的思路和方法,常常不能有效地解决问题[3].动静结合是初中动点问题的突出特点,在分析动点问题时,要结合动点运动的轨迹或规律,分析动点运动到某一状态时出现的特殊位置或数量关系,将运动的点转化为静态的点,以静制动,将运动的问题化为静态的问题,找到解决问题的关键点,然后运用数学知识进行综合分析,这样才能够动静结合,从动中寻找不动,从而有效解决动点问题[4].
例2如图2所示,在长为3■3,宽为3的矩形ABCD中,BC边上有一个动点E,现在连接AE,并将三角形ABE沿着直线AE折叠,使得点B落在图中的F处.
(1)假设动点E运动到BC中点时,将三角形ABE沿着直线AE折叠,判断AE与FC的位置关系.
(2)假设三角形ABE沿着直线AE折叠后,B点落在矩形ABCD的内部点F处,此时CD=FD,则BE的长为多少?
分析(1)判断AE与FC的位置关系,需要利用折叠方面的性质,因此连接BF,得到AE⊥BF,BE=EF,因为E为BC中点,可以得到BE=EF=CE,三角形EBF,FEC为等腰三角形,利用等腰三角形和三角形内角和知识可以判断AE与FC的位置关系.(2)过点F做AB的平行线分别交AD,BC于M,N,利用折叠性质求出AM,FM,FN等线段的长度,然后在直角三角形FEN中,利用勾股定理可以求出FE的长度.
解(1)如图3所示,连接BF交AE于H点,由折叠的性质可知,AE⊥BF于H点,BE=EF,因为E为BC中点,则BE=EF=CE,所以,∠EBF=∠EFB,∠EFC=∠FCE,在ΔBFC中,∠CBF+∠BFC+∠FCB=180°,∠BFE+∠EFC=∠BFC,即∠CBF+∠BFE+∠EFC+∠FCB=180°则∠BFE+∠EFC=90°,所以FC⊥BF,则FC∥AE,因此AE与FC的位置关系为平行.
3巧妙转化,求最值
在初中数学动点问题中,求最值是常见的类型,要求学生能够从不同的层次和角度去思考问题的解决方法,运用数形结合、化归等数学思想,将复杂、运动的问题巧妙地转化为静态的问题,然后依据初中数学知识点有效地解决问题[5].一般来说,应把所求最值问题转化为两点间的距离,然后依据题设条件求取最值.因此,教师要因地制宜,引导学生依据题设条件对问题进行巧妙转化,这样才能够化动为静,有效地解决点点、点线、线线之间的最值问题.
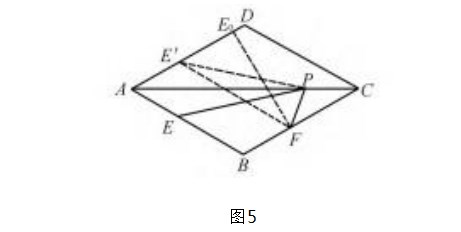
例3在棱长为2的菱形ABCD中,已知∠DAB=60°,AC为菱形ABCD的一条对角线,P为AC上的一个动点,且P不与A,C点重合,E为AB上的一个动点,且E不与A,B点重合,F为BC上的一个动点,且F不与B,C点重合,连接PE,PF,求PE+PF的最小值.
分析本题中有三个动点P,E,F,直接求PE+PF的最小值并不现实,因此需要对问题进行转化,如图5所示,由于E,F在AC的同侧,因此要想求最小值,应该将E,F转化到AC的两侧,通过两点间的线段求最小值,以AC为对称轴做E的对称点E',连接FE',则FE'≤PE+PF,当P点在FE'与AC交点处取等号,这样就将两条线段的长度和转化为一条线段的长度问题,由于ABCD为菱形,当FE'与AD垂直时,FE'的值最小,也就是PE+PF的最小值.
总之,在初中动点问题中,常常包含着丰富的数学思想方法,需要学生能够从不同的角度对问题进行分析和探索,将动点问题转化为静态问题,找准试题的关键点,突破试题的难点,这样才能够有效地解决问题.教师要关注动点问题的育人价值,引导学生以静制动,依据试题的条件和设问的角度,寻找最佳的试题解决思路,强化学生对于数学思想的理解,培养学生的思维能力,帮助学生解决动点问题,提高学生的数学知识综合应用能力.
参考文献:
[1]唐静,姜锐武.探究初中数学中动点问题的解法[J].数学学习与研究,2019(16):122.
[2]黄欲涵.问题特征解读,方法关联探究:以动点线段和最值问题为例[J].数学教学通讯,2022(11):86-88.
[3]曹伟林.例谈初中数学的解题指导策略:以“动点问题”为例[J].数学大世界(上旬),2021(01):69.
[4]赵玉叶.初中数学中“含有一个动点的线段和(差)的最值问题”的解题策略[J].数学教学通讯,2021(32):86-88.
[5]孙世军.浅谈初中数学动点问题的解题策略[J].中学课程辅导(教师教育),2015(23):65.
[6]杨道林.初中数学动点问题解析与思路探讨[J].新校园(中旬),2016(05):107.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/73398.html