SCI论文(www.lunwensci.com):
摘要:相贯线是《工程制图》教学中的重点和难点。针对《工程制图》课程中两立体相交时求解相贯线内容的易懂、难作的特点。本文重点分析了两曲面立体相交时相贯线的不同求解方法。阐述了不同方法求解相贯线的基本原则和适用条件,并结合实例进行分析,以期为学生学习提供思路,提高教学效果。
关键词:工程制图;曲面立体;相贯线
《工程制图》是研究绘制、阅读工程图的理论与方法的学科[1]。是本、专科院校面向机械类、非机械类、水利、土建等各专业大一学生开设的一门重要的专业基础课程,是学习专业课程的基础[2]。各制图课程中均对相贯线内容提出教学要求。虽然不同类型制图课对相贯线要求有差异,但相贯线的教学内容相同[3]。在工程生产实际中,常见两立体相交的实例,例如坝体和闸墩的相贯线,建筑物群的相贯线,机械零件的相贯线等等。但要在图纸上准确表达两立体相交线的投影,在学习过程中要掌握其投影特性和解题方法。
一相贯线的概念及投影特性
两立体相交,也称为两立体相贯,其表面的交线称为相贯线[4]。按照参与相交两立体不同可分为,两平面立体相贯、平面立体与曲面立体相贯、曲面立体与曲面立体相贯三种情况;根据立体相交位置不同可分为,全贯与互贯两种情况,当一立体全部元素与另一立体表面相交时称为全贯,而当一立体部分元素与另一立体表面相交称为互贯;同时还有外表面相贯、内表面和外表面相贯以及两内表面相贯。工程图纸是绘制工程形体的正投影图,因此由于立体的大小、形状和相对位置不同,相贯线的形状也各不相同,在空间中可能是直线段或平面曲线段,也可能是空间曲线段[5]。但根据正投影原理都有共同的三个性质:(1)共有性。相贯线是两个立体的共有线,其投影必在两立体投影的重叠部分范围内。(2)表面性。由于工程制图规定立体都是实体,因此,任何一个立体的轮廓线不能穿过相贯线进入另外立体内部。相贯线是两个立体表面的分界线。(3)封闭性。由于立体是有范围的,一般情况下,相贯线是封闭的。解题时应依据相贯线的投影特性求解。
二教与学中存在的问题
相贯线尤其是两曲面立体的相贯线是工程制图教学中的难点。总结多年教学经验,笔者认为教学学时不够,很难在课堂时间将解题方法讲透,学生需要课前加强预习,课后加强复习,强化练习才能掌握。但由于高等数学等难学课程的学习占用及社团活动的影响,学生没有足够的课外学习时间。加之学生在点、直线、平面和立体的投影特性上掌握不扎实,不牢固,又缺乏空间思维和描述空间形体的能力,学习中存在畏难和抵触情绪[6]。大多数学生能听懂课堂例题,但对相贯线的基本性质和基本投影原理掌握不透彻、不会灵活运用,解题时存在盲目性,容易出错。针对这些教学难点问题,应重视基础理论讲解,强化基本定义、投影性质,通过不同题型深入解读解题方法,杜绝解题过程中出现错误,并重视学生在学习中的主导作用,调动学生积极思考,构建解题思路。
三 相贯线的求解方法
对于两平面立体的相交情况,把平面立体拆分为构成立体的棱面和底面,用贯穿点法或棱面交线法求解。主要依据平面与直线相交求交点和两平面相交求交线的方法。而对于平面立体与曲面立体的相交情况,用截交线的方法,分别求出平面立体上参与相交的棱面或底面与曲面立体表面的截交线,由截交线围成的图形即是两立体的相贯线。但对于两曲面立体相交的情况则要视立体是否具有积聚性、是否具有特殊辅助面和是否轴线相交且同时平行于同一投影面而选择相应的方法。
(一)面上取点法举例
两曲面立体相贯,常见相贯体主要有圆柱与圆柱、圆柱与圆锥、圆锥与球体、圆柱与球体相贯。当参与相交的圆柱体在某一个投影面的投影积聚为一个圆的情况时,首先要强化一个基本概念,牢记求解相贯线过程中的总纲,即相贯线是两立体相交表面公共点的连线,求作相贯线的投影,则是求解两相贯立体表面共有点的投影。因此面上取点法的适用条件是,立体投影具有积聚性。如图1所示,求解大小圆柱的相贯线。首先对题目作形体分析,该形体是由两个圆柱相交而成,小圆柱全部穿过大圆柱,为全贯,由于没有贯穿,因此只有一条相贯线,相贯线为一条封闭的空间曲线;两圆柱对称相贯,呈前后对称和上下对称结构。然后,对形体作投影分析,小圆柱垂直于侧立投影面,其侧面投影积聚为一个圆;大圆柱垂直于水平投影面,其水平投影积聚为一个圆。由于相贯线是两个立体投影的共同部分,既是小圆柱表面的线也是大圆柱表面的线,因此相贯线的侧面投影即是小圆的侧面投影,相贯线的水平投影即是小圆柱的水平投影与大圆柱积聚的圆上共有部分的一段圆弧。由此分析可知,只需求解相贯线的正面投影即可。圆弧是由若干点连接而成。这里必须注意的是两曲面立体上的特殊点,这些相贯线上的控制点包括:曲面立体轮廓线上的点;可见与不可见的分界点;相贯线上最上、最下、最左、最右、最前及最后的点;控制相贯线走向和形状的点。作图求解过程中,先根据积聚投影在左视图中标出小圆柱上最上的点1’’、最下的点2’’、最前的点4’’和最后的点3’’,根据点的三面投影的作图方法作出1、2、4、3,再作出正面投影1’、2’、4’(3’),再根据要求作出若干中间点Ⅴ、Ⅵ、Ⅶ、Ⅷ的正面投影,然后判断可见性,连接成光滑曲线,最后补全图形。尤其要注意的是可见性的判断问题和补全图形的问题,需要明确可见与不可见的分界点,只有在两个立体共同的可见表面上才是可见的,在此例中1’和2’是可见性分界点。要牢固掌握曲面立体的投影特性;补全图形时注意分析和判断曲面立体参与相交的轮廓线上的临界点和没有参与相交的轮廓线是否被遮挡。
(二)辅助平面法举例
圆柱体的投影具有积聚性,而圆锥体与球体的投影不具有积聚性。因此,辅助平面法的适用条件是,当两立体都不具有积聚性时,用辅助平面法求解相贯线,其原理是三面共点。如图2所示,圆锥体投影没有积聚性,若用水平面作辅助平面,则辅助平面与圆柱体的交线是一个圆,与圆锥体的交线也是一个圆,两个交线圆的交点必然是相贯线上的点,即可求解相贯线上的系列点。此时需牢记纬圆法求解圆锥体和球体表面点的方法。若用铅垂面作辅助平面,辅助平面与圆柱体的交线是矩形,与圆锥体的交线是三角形,此时需牢记素线法求解圆锥体表面点的方法。
求解时,首先进行形体分析,该形体是由圆柱体和圆锥体相交而成,不对称结构,圆柱体的部分参与相贯,为互贯,相贯线为一条空间曲线,由于两立体下底面共面,因此不封闭。再进行投影分析,圆柱的水平投影积聚为一个圆,相贯线的水平投影在圆锥的水平投影与圆柱积聚投影的共同部分的圆弧上,只需求解相贯线的正面投影。用辅助平面法求解,辅助平面只能在两立体投影的共同范围内选取,否则失去意义。如图2(a)所示用水平面作辅助面,相贯线上的点为两个圆截交线的交点;如图2(b)所示,用铅垂面作辅助面,相贯线上的点为矩形和三角形截交线的交点。相贯线上的可见性分界点的判断尤为重要,由于圆柱的轴面在前,圆锥的轴面在后,因此可见性分界点3在圆柱的最右边轮廓线上,连线时3’之前的点连成实线,之后的点连成虚线。同时相贯线上的特征点是两立体下底面的交点1和2、圆柱最后轮廓线上的点4和相贯线上的最高点5。再求解若干一般点,连接成光滑曲线。最后要注意的是,补全图形,圆锥左边轮廓线与圆柱重影的部分需要擦去;圆柱最上轮廓线和最右轮廓线与圆锥重影部分需擦去。
(三)辅助球面法举例
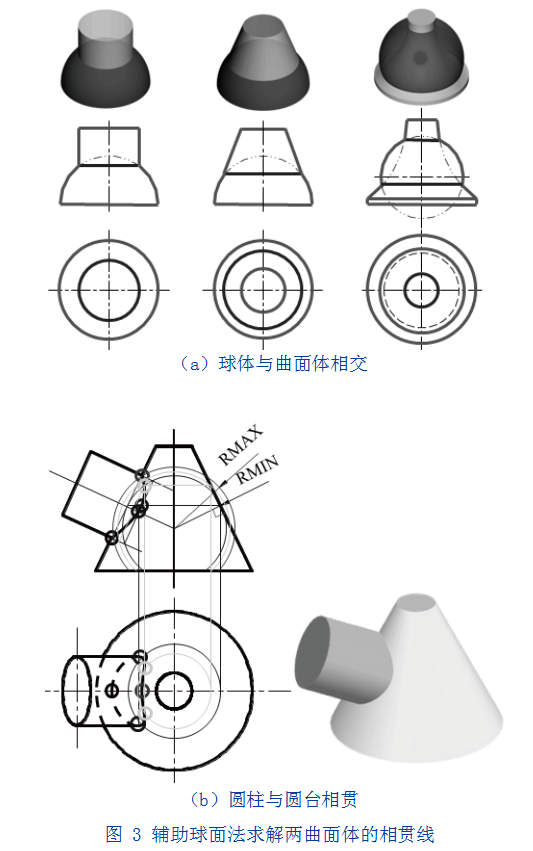
当球体与其他回转体相交时,如图3(a)所示,只要球心在回转体的轴线上,其相贯线必然是与回转轴相垂直的圆。因此,辅助球面法的适用条件是,当两曲面体都是回转体且轴线相交并平行于同一投影面时,用辅助球面法求解相贯线,其基本原理也是三面共点。这里需注意的是辅助球面半径大小范围的选择,辅助球面必须同时与两回转体相交,因此,最大球面极限半径Rmax是以两回转体轴线交点为圆心,两立体轮廓线各交点中最远交点的距离确定;最小极限半径Rmin是由两回转体轴线交点为圆心,向两回转体轮廓线作垂线,其中较长垂线的长度确定。一般情况下,可用最小极限半径确定的辅助球面求解相贯线上某特定方向上的特征点[7]。
如图3(b)所示,首先形体分析,该形体是由斜置圆柱体和圆台相贯而成,圆柱的柱面全部参与相交,为全贯,没有贯穿,因此只有一条相贯线,为空间闭合曲线。两轴线相交,且同时平行于正立投影面,前后对称形体。再进行投影分析,两立体投影都不具有积聚性。用辅助球面法求解,最大极限半径为两轴线交点到两立体轮廓线的交点,最小极限半径是两轴线交点与圆台轮廓线的垂线。辅助球面与圆台交线是水平圆,与圆柱交线是正垂圆,两圆交点即为相贯线上的点,在两极限半径之间作若干辅助球面,作出若干中间点,连成光滑曲线,相贯线正面投影均可见,需要明确水平投影的可见性分界点,是圆柱最前最后轮廓线与最小极限半径确定的辅助球面与圆柱面交线的交点,其上面的点连接可见,下面的点连接不可见。最后,补全图形,主视图擦去圆柱轮廓线与圆台轮廓线的重影部分;俯视图将圆柱最前和最后的轮廓线画至可见性分界点,将圆台下底面重影部分画成虚线。
综上所述,求解两曲面立体的相贯线,通过形体分析和投影分析,选择合适的求解方法。要从基本概念入手,熟悉各方法的适用条件、投影特性和解题步骤,尤其注意特征点的判断和补全图形的绘图,理清思路,前后融会贯通,加强练习,逐步做到熟练掌握、得心应手。
参考文献
[1]任红霞,杨琦琦,孙刚.工程制图课辅助教学实验体系的研究与构建[J].教育与职业,2011,30:160-161.
[2]肖昕迪,吴燕.画法几何与工程制图课程教学改革研究与实践[J].赤峰学院学报,2013,29(4):226-227.
[3]钟宁.截交线与相贯线教学方法浅析[J].现代技能开发,2000(04):101.
[4]殷佩生,水利工程制图[M].北京:高等教育出版社,2015.
[5]刘小年.工程制图[M].北京:高等教育出版社,2004.
[6]欧阳红.制图教学中学生空间想象力的培养[J].长江工程职业技术学院学报,2007(03):79-80.
[7]谷艳华,侯洪生,张秀芝.圆柱与圆锥轴线相交时左侧相贯线上最右点的解析证明与图解[J].工程图学学报,2010,4:146-150.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/7279.html