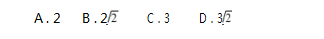SCI论文(www.lunwensci.com)
摘 要 : 重视习题的基础作用和示范引领作用,挖掘习题的深化功能,探索从不同角度和方位 去审视题目,加强知识点之间的覆盖与交汇,追求一题多解,在平时的学习中逐步培养学生解题思维的养成,从而提升解题效率.
关键词 : 一题多解,高考链接,改编延伸
1 问题呈现
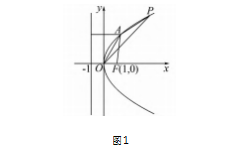
题目 如图 1 所示,已知点 P( 12.43 ) 是抛物 线 C:y2 = 2px(p >0) 上一点,记抛物线 C 的焦点为F,A 为抛物线 C 上第一象限内的一点,若 FA = 7/3则ΔAOP 的面积是 .
2 试题分析
本题以抛物线为题目设计背景,其目的在于考 查学生对抛物线的定义、方程和性质的理解与应用, 通过运用定义法转化是解决此问题的关键所在,同 时在此基础上利用所求点 A 和已知点 P 的坐标及原点 O 为连接枢纽进而达到三角形面积的求解.
3 解法展示
解法 1 由题意知p = 2.所以抛物线的方程为 C:y2 = 4x.不妨设 A(x0 ,y0 ) ,x0 >0.y0 >0.
4 解法辨析
审阅此题不难发现,要解决它需要分两步走.第 一步由题意易得p 的值,即知道了抛物线的方程,结 合抛物线的定义进行转化很容易得出点 A 的坐标, 此时进入解题第二步,围绕由点 O,A,P 所形成的三 角形来求解其面积.解法 1 体现了解三角形思想,重 点依靠余弦定理求其一内角的余弦值达到解决问 题 ; 解法 2 由 O,P 两定点出发得出其直线方程,利 用点到直线的距离求得边 OP 的高而解决问题 ; 解 法 3 充分利用了边 OA,OP 直线的斜率作为铺垫进 而转化到其倾斜角,利用三角形内角是两线倾斜角 的差这一关系来作为解决问题的突破口 ; 解法 4 直 接利用了两条直线的夹角公式结合同角平方和关系 而求得三角形内角的正弦值生成解题方案 ; 解法 5 紧扣点 O,A,P 的坐标进行构造向量的方法来生成 解题思路 ; 解法 6 体现了数形结合与转化的思想.这 6 种解法都是建立在根据题意求得点 A 坐标的前提 下展开的,从其解答过程来看,只是从不同的角度进 行了所学知识的迁移与应用.从题目本身来定位,这 是一道选择题,选择题是一种只显示结果而忽略过 程展示的题型,事实上它对解答者提出了更高、更严 的要求.因此对于选择题的解答一定要树立细审、快思、简算的思想.
细审——— 是指审题要细,要细心推敲题意的层 次关系、逻辑关系、数量关系、已知条件与未知之间 的递推关系,要细心琢磨题意中所蕴含的隐形信息, 通过这些关系和信息要把所学的知识和思想与解答 的问题进行对接与迁移.
快思——— 是指通过审题所得信息要快速和自己的知识储备进行衔接,即通过审题要快速定位出该 题的设计意图和考查方向,要用哪方面的知识去解 答,用什么数学方法和思想来解答,生成解题思路, 形成解题方案.
简算——— 是指解答者对于解决问题的运算过 程一定要简化,以便节省 时 间,同时还要保证解 答的准确性.也就是说对于解题过程只需要把一 些关键数据、关键式子等关键点提炼出来以备后 用,其余的过程全部省略.这就要求解答者务必 要做到心、口、脑、手 四体合一,以求解题过程的 最快化、最优化.
5 高考链接
(2022 年全国高考乙卷( 理、文) 第 5 题) 设 F 为抛 物 线 C: y2 = 4x 的 焦 点,点 A 在 C 上,点 B( 3.0 ) ,若FA=BF,则AB= ().
6 改编延伸
6.1 背景改编
参考文献 :
[1]李旺强.一道圆锥曲线试题的多解、变式与延伸[J].教学考试(理论版) ,2018(20) : 25-26 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/71567.html