SCI论文(www.lunwensci.com):
摘要:思维的广阔性是指思路的广度,思维的包容性往往表现于思维的广度上.广度的特征 在于能形成一群有普遍意义的方法.寻求多种解题途径,通常称为一题多解.一题多解是指对同一 问题能从不同角度、不同侧面去分析和解答.很多数学题目解题方法灵活,注重一题多解的训练有助于培养学生的发散性思维,提高学生的创新能力.本文结合作者的实践教学经验,从一题多解出 发研究如何加强高中数学教学.
关键词:高中数学;思维的广阔性;一题多解;平面向量;解题能力
在数学教学中,广阔性帮助学生从各个条件联系的关键点上,寻求多种解题途径,通常称为一题多解.从高中教育的现状出发,如何结合现有条件,培养学生的数学思维广阔性,是高中数学教学中需要思考的主要问题.一题多解的方法比较适合数学学 习,因为,一题多解能够激发学生的学习兴趣,提高 学生综合应用知识的能力,培养学生的发散性思维. 高中数学教师应该选择难度适中的典型例题,帮助 学生树立起一题多解的意识和善于利用发散性思维 的习惯,以提高学生思维的广阔性.下文就以平面向 量的问题在课堂教学中得到的解答展开论述.
老师:昨天请同学们已经思考了这一题,是否得到 解决?
学生 A 举手并到黑板上讲解.
老师:你怎么想到此思路?
→ → →
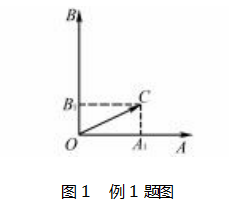
学生 A:画出草图便可看出,所求的关键是向量OC在向量OA与向量OB方向上的分解情况,想到平面向量的基本定理的运用;再由平面向量的加法法则、共线性质就解出这个题了.
此时,学生 B 举手并到黑板上讲解.
老师:你又是怎么想到此思路
→ → →
学生 B:由于点 C 在∠AOB 内且∠AOC = 30 ° , 故把 C 点放在线段 AB 上也满足已知条件.画出草图便可看出,向量OC在向量OA与向量OB方向上的 分解情况,想到平面向量的基本定理的运用;再由平 面向量的加法法则、共线性质就解出这个题了,而不 需要设参数 r.
此时,学生 C 迫不及待地举手.
老师:你又是怎么想到此思路?
→ → → → →
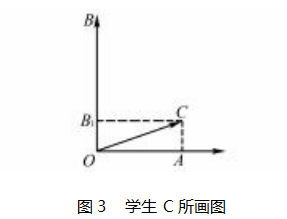
学生 C:由于点 C 在∠AOB 内且∠AOC = 30 ° , 故假设 C 点在直线 OA 上的投影即为点 A , 也满足已知.画出草图便可看出,向量OC在向量OA与向量OB方向上的分解情况,关键是找OB1 与OB的关系,便可 求解.而不需要设参数 r , 也比刚才那位同学的解题 思路更简捷.
此时,教室里响起了热烈的掌声.学生 D 举手, 并谦虚地说:我的思路也许不比他们的简单,但可以让同学们进行另类思考.
老师:你又是怎么想到此思路?
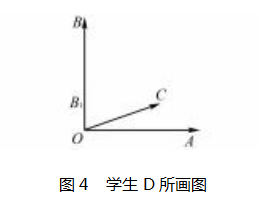
学生 D:由于在证明正弦定理的时候,构造了向 量j , 利用数量积,从而让定理获得证明.观察所求是

, 故由已知的向量式想到了数量积,找到了此解法.
此时,教室里的掌声更热烈、更持久,同学们脸 上有的绽放出了微笑,有的频频点头.学生 E 举手, 教室里发出了惊奇声,难道还有解法? 学生 E 说:同学们,我进行的也是另类思考.
老师:你又是怎么想到此思路?
学生 E:我们在前面学习了平面向量的坐标运 算,故想到利用向量垂直建立平面直角系,把涉及到 的向量都用其坐标表示出来,使较抽象的平面向量 与坐标发生联系,从而转化成了坐标运算.
此时,教室里掌声雷动,一片哗然.
老师:此题目同学们思考得非常到位,我受益匪 浅.但在解决完一个问题后,最难得的是回头一看.
当把已知条件

改为
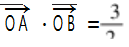
,此时

,“ 学生 E”的解法仅靠教科书上 的知识较 难 以 解 决.从 前 面 五 位 同 学 的 解 法 中, 作为小题寻求既准确又简洁和快捷的方法是“ 学 生 C”的解法,最常用的方法是“ 学生 A ”,“ 学生 D ”的解法也是通法.这是同学们的思考引发了我 的简单思考.
通过本堂习题课,充分展现了学生思维的广阔 性及一题多解和发散性思维,只要教师能把课堂时间还给学生,学生就能够从不同方面、不同视角来分析问题,并运用多种解题方法来解决问题.数学相比其他学科,并不是一个注重记忆知识点的学科,其更加注重对学生知识运用能力的考查.提高运用能力的前提就是提高思维能力.一题多解就是让学生明 白可以通过不同的方法取得同一个结果,打破学生对知识的固定认知,增强学生主动探究学习的兴趣. 通过一题多解方法的训练可以使学生灵活运用各 个知识点,深入掌握各个知识点之间的内在联系, 加深对数学思想和数学思维的理解,提高思维的 广度,也有助于培养其发散性思维.学生具备了举一反三的思维后可以延伸到其他学科的学习中去,使其在解题能力和学习能力方面都得到提高. 当然一题多解更需要得到教师的正确指导,避免盲目性地思考使学生丧失学习的兴趣及养成不正确的思考习惯.
随着高中课程改革的不断推进,对培养学生发 散性思维能力方面的考查也越来越多,在命题形式 上也越来越倾向于选择那些利用发散性思维的题 目.教师是高中教育的主要力量,在日后的教学中应 该树立起创新性教学的意识,善于利用一题多解培 养学生思维的广度,从而提高学生的解题能力.
参考文献:
[1] 杨静雅.高中数学解题过程中培养学生的反思能力的研究[ J].中外企业家,2020(15):229.
[2] 孔令昂.如何在高中数学解题教学中培养学生反思能力[J].数理化解题研究,2021(27):34-35.
[3] 何苏晋.关于如何引导学生对数学解题进行反思[ J].新课程( 中学),2017(11):152.
[4] 郑波.高中数学解题教学培养反思能力“ 三 策略”[ J].数学教学通讯,2020(15):77 -78.
[5] 姜德祥.浅论高中生数学解题反思能力的培养[ J].教师,2013(22):71 -72.
[6] 陶尚明.在高中数学解题中培养学生的反思能力[ J].数理化解题研究,2021(13):11 -12.
[7] 金曦东.高中数学解题过程中培养学生的反思能力的探究[ J].数学学习与研究,2021(25 ):22-26.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/71074.html







 , 故由已知的向量式想到了数量积,找到了此解法.
, 故由已知的向量式想到了数量积,找到了此解法.

 改为
改为 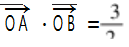 ,此时
,此时 ,“ 学生 E”的解法仅靠教科书上 的知识较 难 以 解 决.从 前 面 五 位 同 学 的 解 法 中, 作为小题寻求既准确又简洁和快捷的方法是“ 学 生 C”的解法,最常用的方法是“ 学生 A ”,“ 学生 D ”的解法也是通法.这是同学们的思考引发了我 的简单思考.
,“ 学生 E”的解法仅靠教科书上 的知识较 难 以 解 决.从 前 面 五 位 同 学 的 解 法 中, 作为小题寻求既准确又简洁和快捷的方法是“ 学 生 C”的解法,最常用的方法是“ 学生 A ”,“ 学生 D ”的解法也是通法.这是同学们的思考引发了我 的简单思考.