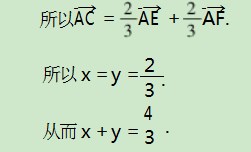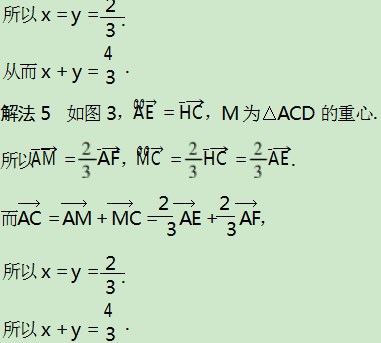SCI论文(www.lunwensci.com)
摘要:一题多解就是从不同思路、不同角度出发,运用不同的方法解答同一问题的思维活动.在解题时渗透一题多解的策略,对培养学生的发散性思维具有很大的帮助.
关键词:三角形法则,平行四边形法则,向量基本定理
题目呈现
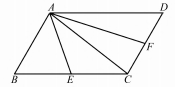
例1如图1,已知口ABCD,E,F分别为BC,
CD的中点,若=x+y,则x+y=.
向量既有大小又有方向,既能像实数一样进行运算,又有直观的几何意义,是数与形的完美结合.向量的加减法是向量运算的基本内容,它们反映了图形的基本结构和图形的基本性质.向量运算的代数表示形式使得向量成为沟通几何与代数的重要工具,因此向量的运算也就成了考查的重点内容.
2题目解析
解法1直接利用向量的三角形法则和平行四边形法则求解.
AC=向量AE+向量EC=向量AE+1/2向量AD,如图3
解法3利用中位线构造平行四边形解决.
如图2,取AC中点O,连接OE,OF,则四边形OECF是平行四边形.
于是向量0E+向量OF=向量OC解法4
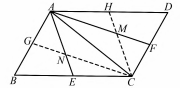
利用三角形中线交点即重心的性质求解.如图3,取中点H,G,连接CH,CG,分别交AF,AE于点M,N.于是M
N分别是ΔACD,ΔABC的重心.
解法6利用三角形中线对应的向量是两边对应向量之和的一半求解.
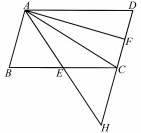
如图4,延长AE交DC延长线于点H,则C为HD中点,E为AH中点.
解法9利用三角形中线性质及平行四边形法则求解.
因为E是ΔABC的边BC的中点
解法11利用填空题的特点特殊图形法求解.
在平时的教学中渗透一题多解思想,能很好地帮助学生构建更加完善的知识体系,能使学生的思维更开阔、更清晰,从而更加灵活地把握知识间的横向关系与纵向关系,切实提高学生分析问题、解决问题的能力.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/70323.html