SCI论文(www.lunwensci.com):
摘要:弹簧连接体问题是近年高考的热点问题,此类模型多涉及对动量、能量问题的综合考 查,运动过程和运算过程都比较复杂.本文通过转化参考系,研究微过程,结合图像和过程的对称 性,研究了 2022 年全国乙卷 25 题,给出了本题的几种快速解法.在此基础上,本文强调复习过程中应注意物理学科思想的渗透,从而有效地发展学生的学科核心素养.
关键词 : 质心参考系, 微元法,对称性
高考真题中蕴含着丰富的物理学科思想,深入研究真题,尤其是压轴大题,有助于教师准确把握高考考查方向,改进教学行为,提升课堂教学实效. 2022 年高考全国乙卷的 25 题就是一道学科思想丰 富的好题,值得深入钻研.本文通过一题多解的形 式,展示其背后的物理思想,有利于在课堂上开阔学生眼界,提升学生的学科核心素养.
1 题目呈现
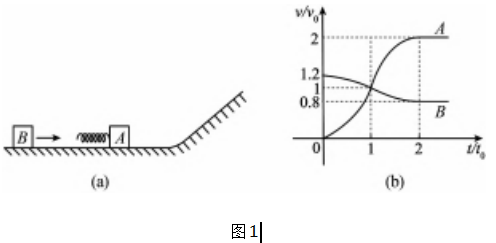
(2022 年全国高考乙卷 25 题) 如图 1(a) ,一质 量为 m 的物块 A 与轻质弹簧连接,静止在光滑水平 面上 ; 物块 B 向 A 运动,t = 0 时与弹簧接触,到 t = 2t0 时与弹簧分离,第一次碰撞结束,A、B 的 v -t 图 像如图 1(b) 所示.已知从 t = 0 到 t = t0 时间内,物 块 A 运动的距离为 0.36v0 t0.A、B 分离后,A 滑上粗 糙斜面,然后滑下,与一直在水平面上运动的 B 再 次碰撞,之后 A 再次滑上斜面,达到的最高点与前一次相同.斜面倾角为 θ(sinθ = 0.6) ,与水平面光滑连接.碰撞过程中弹簧始终处于弹性限度内.求 :
(1) 第一次碰撞过程中,弹簧弹性势能的最大值 ;
(2) 第一次碰撞过程中,弹簧压缩量的最大值 ;
(3) 物块 A 与斜面间的动摩擦因数.
2 试题精析
本题是常见弹簧碰撞模型,属于学习探索类情境.
作为甄别最优秀学生的压轴大题,本题的设问 比较创新,尤其是第(2) 问,由于不是常见的运动形式,不能直接用运动学公式求解 ; 也不宜用所谓的 “平均速度” ,含混地表述物体对地位移.笔者认为 应该运用守恒定律或对称性,结合微元法对微小 位移进行分析,再累计求和,从而得到对地位移. 这一过程 的难点在于,对于微小位移的分析容 易 造成失误.第(3 ) 问,是对于能量、动量、动能定理 等必备知识的综合考查,计算难度较大,在考场上不易解得.
下面尝试采用多种解法,从多个角度分析本题,展示探讨题目背后所蕴含的学科思想.
2.1 解析第(1) 问
解法一 (动量-能量双守恒) ( 略)
解法二 (质心参考系、柯尼希定理) A、B 质心位置
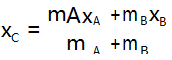
,质心速度
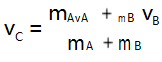
由图像知 : vC = v0 ,vB = 1.2v0 ,vA = 0,解得 : mB = 5m.
由孤立二体系统的柯尼希定理 :
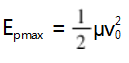
相(其中折合质量
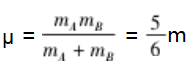
相对初速度 v0相= vB -vA = 1.2v0 ) ,解得 :
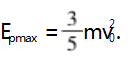 2.2 解析第(2) 问
2.2 解析第(2) 问
解法一 (微元法 + 守恒律) 物块 A、B 通过弹 簧发生相互作用,做变加速运动,应选用动量守恒定 律和微元法解题.共速时,弹簧压缩量最大,最大压缩量即 A、B 的相对位移.
在任意时刻 t 时,A、B 速度分别为 vA 、vB.由动 量守恒 :
mAvA + mBvB = (mA + mB ) v0 ,即 : vA + 5vB = 6v0 .
取一段极短 时 间 Δt,A、B 可视为匀速直线运 动,各自位移为 : ΔxA = vAΔt,ΔxB = vBΔt,
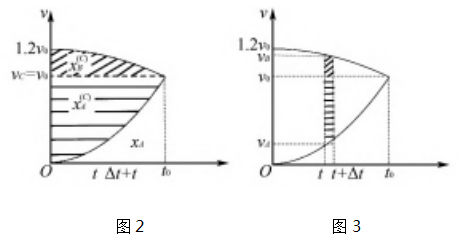
两者相对位移 Δx( 即图 2 中的阴影部分面积) : Δx = ΔxB - ΔxA = 1.2v0Δt -1.2ΔxA,
由题中条件,0 -t0 时间内,xA = 0.36v0 t0 ,对上 式累计 :x = 1.2v0 t0 -1.2xA = 0.768v0 t0 .
解法二 (转换参考系) 由 A、B 任意时刻动量守恒,mAvA + mBvB = (mA + mB ) v0 ,变形得 :
mA ( v0 -vA ) = mB (vB -v0 ) .
可取以 v0 向右匀速运动的参考系 C.在 C 中, A、B 的速度记作 v
A= vA -v0 、v
B = vB -v0 .
则有 : v
A = -5v
B,则极短时 间 Δt 内,位移有 :Δx
A = -5Δx
B ,累计求和,位移大 小有 : x
A = 5x
B,( 如图 3 中阴影部分比值为 5: 1)
由图 像 x
A = v0 t0 - xA = 0.64v0 t0. 则 x = 0.128v0 t0 ,相对位移 x = x
A + x
B = 0.768v0 t0 .
解法三 ( 质心运动) 系统不受外力,A、B 质心将以 v0 做匀速运动,xC = v0 t0.质心位移满足 xC =

,xA 、xB 为 A、B 的 对 地 位 移,xA =0.36v0 t0 ,解得 xB = 1.128v0 t0 ,相对位移 x = xB -xA =0.768v0 t0 .
2.3 解析第(3) 问
解法一 (动量 -能量双守恒) 物块 A 第二次 到达斜面的最高点与第一次相同,说明物块 A 第二 次与 B 分离后速度大小仍为 2v0 ,方向水平向右动 量守恒定律、能量守恒定律得 : μ = 0.45
解法二 (质心系中的弹性碰撞) 设A 返回后,对地速度大小为 vA1 ,B 与之碰前速度 vB1 = 0.8v0 .
取 A、B 质心系为 D 系,

; 亦即 :
vA1 -vD = -5(vB1 -vD ) ①
A 与 B 第二次弹性碰撞后,设 A、B 对地速度分 别为 vA2 、vB2.显然必须有 vA2 = 2v0 ,A 才能返回相同 高度.
在 D 系中,弹性碰撞有 :
vD) 1 = -v) ,即 vA1 -vD = - (vA2 -vD ) ②
②代入① , 解得 vD = 0.5v0 ,vA1 = -v0 .
由 A 上,下斜面位移大小相等得 :

解得 : μ = 0.45.
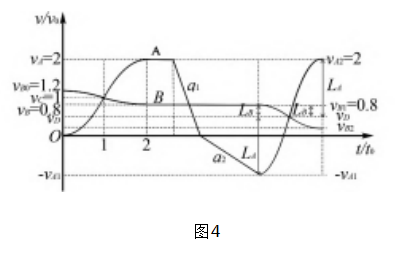
解法三 ( 图像法 + 对称性) 由题目中 0 -2t0 时间内图像可知,弹性碰撞有如下特点 :
(1) 每个物体碰前 v前 、碰后速度 v后 关于共速 v共 对称,即 : v前 -v共 = v共 -v后 ;
(2) 碰前、碰后速度偏离共速的大小与质量成反比,即 : mA (mA -m共 ) = mB (mA -m共 ) .
定性画出之后的图像( 如图 4 ) ,由对称性得 : mALA = mBLB,即 :2-vD = 5(0.8-vD ) ,则 vD = 0.5v0 . LA = 1.5v0 ,LB = 0.3v0 ,vA1 = v0.之后同“解法二”.
3 探讨本题物理思想及教学启示
高考评价体系明确指出,高考题的核心功能是 立德树人、服务选材、引导教学.本题中所蕴含的物 理思想的确值得我们深入思考,从而更好地将其融入到我们的日常教学之中.
3.1 守恒思想
本题每一问都有对守恒思想的重点考查,但角 度不同各有侧重.可见,高考对于如能量观念、守恒 思想等基础性必备知识的考查是不遗余力,我们应 该在新课教学和复习过程中更加重视基础知识的生 成,以及在各种真实情境下的呈现,促进物理观念的
立体化生成.
3.2 微积分思想
本题第(2) 问颇为创新,意料之外但又情理之 中.教材关于微积分思想的渗透是循序渐进的,例如 在“平均速度和瞬时速度”中初次展现微元思想; 又如运用微积分思想,结合 v -t 图像推导匀变速运动位移公式 ; 再如,结合 F -x 图像,探究弹性势能的 表达式.在相关的不同章节之中反复使用,我们应注 重微积分思想培养的连续性,使学生由衷地欣赏,自然地接受,全面的掌握,并主动地运用这一重要思想.
3.3 对称思想
题( 1) - (3) 问均可由对称性,得到简便解法. 题目以图像的形式给出了条件,从中很容易看出关 于共速速度( 即质心速度) 的对称性 ; 在弹性碰撞 中,由对称性替代能量守恒,直接从相对运动的对称 入手,使问题得到快速地解答.事实上不仅是碰撞问 题,在很多问题的教学中,我们都能从对称性的角
度,为学生展示更加清晰的物理图景.
3.4 等效思想
本题多次出现利用质心的相关性质和定理的解 法,是因为这样能够将复杂物体运动,等效为“质心的 匀速直线运动 + 相对质心的简谐振动” ; 另外,质心承 担了系统的总动量,那么相对于质心的总动量即为零; 再者,由于质心匀速运动动能不变,那么就只有相对质 心的能量可供使用( 资用能) 等,以上都是等效思想很 好的应用.等效思想作为“化繁为简”的重要物理思想,出现在物理学习的诸多章节,值得我们更多地关注.
总之,本题以常见的模型作为压轴大题,兼具基 础性和创新性.其熟悉的情境符合学生的学习实际, 设问上的创新能有效增加试题的区分度.在日常教 学中,作为教师不仅要明白知识、规律的来龙去脉, 更应该引领学生关注题目所蕴含重要的物理思想. 因此,强调基础模型的研究,拓展知识的内涵外延, 重视其中物理学科思想的培养,应是一条提升学生的物理学科素养的有效途径.
参考文献 :
[1]赵凯华,罗蔚茵.新概念物理教程·力学( 第二 版) [M].北京: 高等教育出版社,2004 .
[2] 中华人民共和国教育部.普通高中物理课程标 准(2017 年版) [M].北京: 高等教育出版社,2017.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69893.html
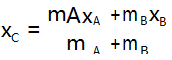 ,质心速度
,质心速度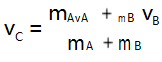 由图像知 : vC = v0 ,vB = 1.2v0 ,vA = 0,解得 : mB = 5m.
由图像知 : vC = v0 ,vB = 1.2v0 ,vA = 0,解得 : mB = 5m.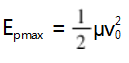 相(其中折合质量
相(其中折合质量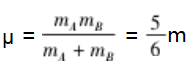 相对初速度 v0相= vB -vA = 1.2v0 ) ,解得 :
相对初速度 v0相= vB -vA = 1.2v0 ) ,解得 :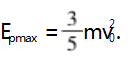
 解得 : μ = 0.45.
解得 : μ = 0.45.