SCI论文(www.lunwensci.com)
摘 要 : 卫星从圆轨道变轨为椭圆轨道涉及圆周运动和离心运动、加速度与向心加速度这些概念的理解,本文从常见的错误解析出发,通过概念分析和数学推导,说明在卫星变轨的问题中,变轨前后在轨道相切点的向心加速度不变.
在卫星变轨模型中,变轨前后卫星向心加速度 的变化,是我们在教学中常常遇见的问题,也是学生常常疑惑不解、容易出错的问题.
1 问题引入
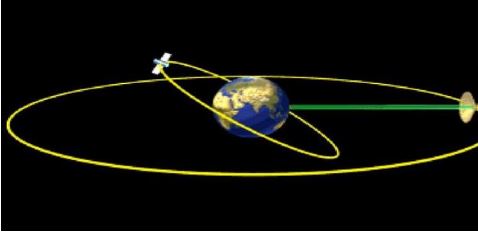
如图 1 所示,在近地圆轨道 Ⅰ( 到地心的距离 为 r1 ) 上运行的卫星接到变轨指令后,在 A 处进行 短暂时间的加速过程,速度从 v 增大为 v1 进入椭圆 转移轨道Ⅱ(远地点到地心的距离为 r2 ) ,请问从圆 轨道Ⅰ经过 A 点的向心加速度 an 与从椭圆轨道Ⅱ 经过 A 点的向心加速度 a 'n 谁大?
2 错误解析
错误解析 1 卫星在圆轨道上经过 A 点时受万有引力 F万 = Fn = m r1(v2) ,变轨时速度增大,万有引力F万 < 向心力 Fn,故从圆轨道 Ⅰ经过 A 点的向心加 速度 an 比从椭圆轨道Ⅱ经过 A 点的向心加速度 a 'n小,即 an错误原因 : 物体做匀速圆周运动和离心运动的 条件未理解透彻.做圆周运动的物体由于惯性,总有 沿着切线方向飞出去的倾向,但物体没有飞出去,这 是因为外力拉着它,满足了它做圆周运动对向心力 的需求,即 F供 = F需.卫星在圆周运动轨道上时,F方即为 F供,恰好满足卫星以 v 绕地球做半径为 r1 的
5 教学启示
万有引力为向心力,在万有引力的作用下,卫星 的轨道既可以是圆周也可以是椭圆.运动到同一位 置处时的受力总是相同的,由牛顿第二定律可知加 速度也是相同的,这与卫星的运动状态无关.而在椭 圆轨道的近地点和远地点处,速度方向与受力方向 垂直,卫星的向心加速度即是加速度,因此在变轨前 后瞬间,加速度和向心加速度均是相同的.利用所学 知识进行数学推导的过程,有助于帮助学生培养模型构建和科学思维的学科素养.
参考文献 :
[1] 申传领.相切轨道切点处加速度、向心加速度的 辨析[J].中学物理教学参考,2019 (48 ) : 18 -20 .
[2]邵云.椭圆曲率半径的四个公式及两种力学推理方法[J].物理与工程,2019(6) : 103 -107 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/69553.html