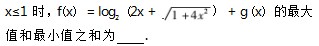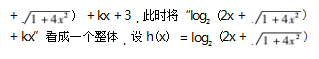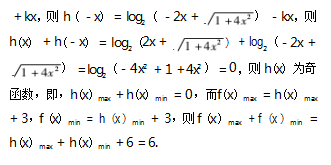SCI论文(www.lunwensci.com)
摘 要 : 整体思想是一种重要的解题思想.高中数学解题中注重应用整体思想可更好地理清运 算对象之间的内在逻辑,低运算复杂度,提升运算效率.高中数学教学中应注重为学习者展示如何 借助整体思想走出数学解题困境,提高学习者整体思想应用意识,给其以后更好地应用整体思想灵活解题奠定坚实基础.
关键词 : 整体思想,高中数学,解题,困境
众所周知,高中数学习题情境复杂多变.要想成功、顺利地解题,不仅需要牢固地掌握基础知识, 更要了解与掌握数学思想应用意识.其 中整体思 想在高中数学解题中有着广泛地应用,教学实践 中应注重结合具体教学内容做好整体思想在解题 中的应用讲解,更好地激活学习者的解题思维,提升其解题能力.
1 借助整体思想,解答函数习题
函数是高中数学的重要知识点,相关习题更是 复杂多变.解答函数习题常使用函数的相关性质.对 于部分函数习题需要运用整体思想,对要求解的问 题进行处理.教学实践中,为使学习者能够运用整体 思想走出解题困境,一方面,为学习者灌输整体思想 相关理论,使其认识到什么是整体思想,运用整体思 想解答函数习题的必要性,无形之中认识到整体思 想的重要性 ; 另一方面,为使学习者更好地掌握整体 思想解答函数习题的相关思路以及相关应用技巧, 避免在应用的过程中走弯路,课堂上应注重与学习 者一起剖析典型习题,尤其鼓励学习者积极开展讨 论活动,思考将哪一部分当做一个整体,以更好地应用函数相关知识,给学习者留下深刻印象的同时,迅 速地找到解题的突破口.例如在完成函数奇偶性内 容讲解后,课堂上与学习者一起剖析如下习题,使学 习者认识到遇到较为复杂函数解析式的问题时,应 通过整体思想的应用巧妙地转化,减少不必要地运 算,迅速解题.
例 1 已知函数 g(x) 为一次函数,对任意的实 数 m、n,满足 g(m + n) = g(m) + g(n) -3.当-1 ≤
解析 观察可知函数f(x) 的解析式较为复杂, 而且 g(x) 从题干给出的条件中无法求得 g(x) 具体 的解析式,因此,不能直接运用其单调性求解最值. 该题看似无从下手,但是从函数奇偶性角度分析,运 用整体思想不难得出正确结果.
根据题意设 g(x) = kx + b,因 g(m + n) = g(m) + g(n) -3.代入得到 k(m + n) + b = k(m + n) + 2b - 3.易得 b = 3.即 g(x) = kx + 3.则f(x) = log2 (2x
2 借助整体思想,解答解三角形题
高中数学中解三角形题,主要运用三角函数与 正弦、余弦定理.但是解答部分习题时,仅仅掌握三 角函数相关知识并不能有效地求得正确结果.原因 在于部分学习者在运算的过程中不注重整体思想的 应用,计算过程中走了不少弯路.为避免学习者出现 这一情况,应结合自身教学经验以及学习者的实际 情况,为学习者做好借助整体思想解答三角函数习 题的讲解.
例 2 已知 ΔABC 的周长为 1 +根号2 且 sinA +sinB = 根号2sinC.若 SΔABC =1/6sinC,则 C 的 大 小 为 _____.
解析 该习题较为常规且难度不大.解题的关 键具备整体思想应用意识,在整体思想指引下开展 运算.另外,根据经验遇到求三角形的习题时,首先 想到需要运用正弦、余弦定理实现边和角的互化.在 此基础上对给出的已知条件进行整理,转化,并认真 观察各关系式,运用整体思想降低计算难度.
3 借助整体思想,解答不等式习题
“不等式”是高中数学较为基础的知识点,是高 考的热门考点.部分习题技巧性较强,解题时若不能 运用正确的解题思想便难以有效地切入.根据经验 解答相关习题不仅要联系不等式的相关性质,以及 相关运算公式,而且还应注重对已知条件进行适当 转化.必要情况下,运用整体思想将其中的一部分看 成一个整体,通过巧妙的代换减少参数的同时,直观 地揭示出相关参数之间的联系,为更好地运用不等 式相关运算公式奠定坚实基础.
例 3 已知 a、b、c 均为大于零的数,且满足 a2 + 2ab + 2ac + 4bc = 12.则 a + b + c 的最小值为 .
解析 看到给出的参数均为正数,根据经验需 要应用基本不等式知识.但是看到给出的已知条件, 很多学习者因不会转化而一头雾水.事实上解答该 题需要具有较强的观察以及分析能力,采用整体思 想进行参数的巧妙代换,减少参数个数向基本不等 式靠拢.
4 借助整体思想,解答向量习题
向量在高中数学中占有重要地位.其涉及的概 念以及运算公式较多,且与其他知识点有着密切的 联系,因此习题类型非常之多.部分习题以向量为背 景考查学习者的运算能力.解答该类问题尤其不能走入出题人设计的陷阱之中,应注重保持清醒的头 脑,通过整体思想的应用,将看似复杂的问题简单 化,提高运算效率.
例 4 已知 e1 ,e2 为平面内的单位向量,且存在 关系式| 2e1 -e2 | ≤ ■/2,若 a = e1 + e2 ,b = 3e1 + e2 ,向 量 a,b 的夹角为 θ , 则 cos2 θ 的最小值为 .
解析 该题要求两个向量余弦的平方值,涉及 的参数较多,计算量较大.如采用整体思想,可很好 地简化计算,提高解题正确率.
5 借助整体思想,解答导数习题
“导数”是高中数学的难点,是高考的必考知识 点.部分习题难度较大,没有较强的综合能力,难以 求解出正确结果.部分高中导数习题综合性较强,需 要学习者灵活运用多种解题思想,尤其通过整体思 想的应用,可确保问题得以顺利解答.
例 5 已知f(x) = xex -ax2 ,g(x) = lnx + x-x2+ 1 -e/a.若当 a>0 时,h(x) =f(x) -ag(x) =0 恒成立,则实数 a 的取值范围为 .
解析 该题属于导数部分难度较大的题目.解 题的关键在于等价转化,并运用整体思想化繁为简, 而后借助导数知识以及函数图象,找到解题切入点.
根据题意 a>0 时,h(x) = xex -ax2 -a( lnx + x- x2 + 1 -e/a) =0.整理得到 : xex + e =a (x + lnx + 1) ,由 x = elnx ,可得1/e,ex + lnx + 1 + e =a(x + lnx + 1) , 此时式子较为繁琐,可将“x + lnx + 1 ”看成一个整 体,令 t = x + lnx + 1.则 t ∈R; 上述不等式转化为 et-1 + e=at,t∈R; 令 m(x) = ex-1 + e,n(x) = ax,要 想满足题意函数 m(x) 图象始终在函数 n(x) 的图象 之上.设直线 n(x) = ax 和函数 m(x) 图象相切于点 (x0 ,ex0- 1 + e).而 m ' (x) = ex-1 ,则过点(x0 ,ex0- 1 + e) 的切线方程为 y - (ex0- 1 + e) = ex0- 1 (x-x0 ) ,该切 点过原点时将(0.0) 代入得到 : ex0- 1 (x0 -1) = e,即 x0 = 2.即,m ' (2) = e ; 因此,a 的取值范围为(0.e].
通过讨论不难得出,在很多的高中数学习题解 答过程中都能看到整体思想的身影,整体思想在整 个高中数学中的重要性不言而喻.高中数学教学实 践中为使学习者认识、理解、掌握借助整体思想在解 答不同数学习题时的相关技巧,在讲完数学理论基 础后,应结合教学进度,通过相关例题为学习者做好 应用性示范,将相关应用细节考虑到位,有效提升学 习者的解题能力.
参考文献 :
[1]梁卫祥.例谈整体思想在高中数学解题中的应 用研究[J].高中数理化,2021 (S1) : 21 .
[2]杨则平.高中数学解题中整体思想的应用[J]. 数理化解题研究,2021 (31) : 53-54 .
[3] 王立嘉.整体思想在高中数学解题中的应用[J].中学数学教学参考,2021 (09) : 37-39 .
[4]廖秀华.借助整体思想 助力数学解题[J].数 理化解题研究,2021 (16) : 14 -15 .
[5]杨文博.例谈整体思想在高中数学解题中的应用[J].数学学习与研究,2020(11) : 31-32 .
[6] 陈莉莉.整体思想巧用于高中数学解题[J].理 科考试研究,2019.26(21) : 35-36 .
[7]林锦霞.整体思想在高中数学解题中的应用讨 论[J].高考,2018(06) : 233 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/68842.html