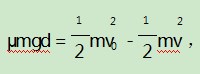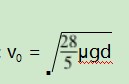SCI论文(www.lunwensci.com)
摘要:动量守恒定律表现在于物体和物体的相互作用过程中,发生的机械运动量传递问题的规律.动量守恒原理是高考考查的重点,也是考查考生推理能力和综合分析能力的重点内容,历年高考中考查动量守恒问题都十分灵活,其通常与其它重要的知识相结合出题,综合性强.因此,动量守恒求法是考生比较需要注意的问题,若熟悉掌握好动量守恒的求解方法,可以提高解题正确率和效率.现将高考中常见的动量守恒定律问题结合具体例题,讨论如何解决动量守恒定律的问题,通过详细的解答步骤帮助同学们学习和掌握这类问题,灵活运用不同思路使同学们更透彻地理解动量守恒定律的问题.
关键词:动量守恒;模型;解题技巧
1考查动量守恒定律与动能定理结合问题
例1假设先将2个不运动的小球B和C放在一个表面不光滑的水平地面上,又将两个小球放在距离为d的位置上.在实验开始的时候,小球B最开始的速度为v0,之后让小球B与小球C进行弹性正面的相撞,将两个小球相撞的时间控制在十分短的时间内,在实验结束后两个小球都静止的时候,这两个小球相距的位置还是为d.当我们知道两个小球与地面之间的动摩擦因数都是μ,mC=2mB,重力加速度大小为g.求v0的大小.
解析设两个小球还没有相撞到的时候,小球B的速度为v,在两个小球相撞到之后,小球B的速度为v1和小球C的速度为v2,在两个小球相撞的这个过程当中,可以根据能量守恒定律和动量守恒定律得:
其小球B被撞到之前的速度方向为正.两个式子连结解得
设相撞之后B的运动距离为d1和C的运动距离为d2,
根据动能定理得:
以及根据题目已知条件可知:d=d1+d2,
B开始的速度为v0,
又根据动能定理得:
式子连结解得:
2以弹簧碰撞及爆炸为模型的动量守恒问题
例2如图1,在表面光滑的地面上放两个一样的木块P1、P2,质量均为m.一根轻质弹簧固定在P2的最右边,P2的最左边A在轻质弹簧的自由端B距离为L的位置上,在P1的最右的位置放一块小黑块P,小黑块P可以当成质点,mp为2m.让木块P1与小黑块P以一个共同的速度v1向右运动,让木块P1与小黑块P碰撞不运动的木块P2.相撞的时间控制在十分短的时间内,在相撞之后,木块P1与木块P2连接到了一起,成为了一个部分.小黑块P在压缩弹簧之后被弹回并在A点停了下来,(弹簧始终在弹性限度内).小黑块P与木块P2两者之间的动摩擦因数是μ.求:
(1)刚相撞完时,木块P1与木块P2的共同速度v2和小黑块P的最终速度v3;
(2)在P压缩弹簧的过程中最大压缩量x和其对应的弹性势能EP.
3与动量守恒定律有关的实验问题
例3如图2所示,下面的实验中,我们想要直接将两个小球a、b相撞之前和两个小球a、b相撞之后的速度测出是很困难的.所以可以通过测量出()间接求出两个小球a、b相撞之前和两个小球a、b相撞之后的速度.
A.h:最开始时,小球从所在位置落下的高度
B.H:小球被抛出的时候,距离地面有多远
C.X:小球做平抛运动的时候,小球射出去的距离
解析我们可以看到在实验当中的相撞是控制在同一个位置上的,所以在空中停留的时间也是相同的,根据小球做平抛运动的时候,小球射出去的距离即可求出相撞后速度大小的比值,从而求出两个小球a、b相撞之前和两个小球a、b相撞之后的速度.因此,选C.
例4根据图3,小球在最初位置被抛出去的时候,在地面上产生一个的垂直投影为点O.在实验过程中,首先在斜面轨道上的S位置反复的将射球m静止释放,之后观察射球m落地点平均所处的位置P,测量出平抛射出去的距离OP.之后,在轨道的水平部分放置一个被碰的小球m1,在斜面轨道上S位置上让入射球m从静止状态运动,使入射球m与小球m1相碰撞,并将该过程多次重复.之后一定要达到的做法是().
A.m、m1:用测量工具测出2个小球分别的重量
B.h:实验开始时,小球m从所在位置落下的高度
C.H:小球被抛出的时候,距离地面有多远
D.M、N:分别找出m、m1相撞之后落地点平均所处的位置
E.OM、ON:测量出平抛射出去的距离
解析这次实验当中,一定要用测量工具测出2个小球的质量m、m1,分别找出m、m1相撞之后落地点平均所处的位置M、N以及测量平抛射出去的距离OM、ON,所以选择ADE三个选项.
例5若两球相撞之前和相撞之后的动量守恒,则表达式是(用例题2中已知的量表示)﹔若两球相撞是弹性碰撞,那么应该还满足的表达式是(用例题2中已知的量表示)
例6根据测定的结果,得出m=45g,m1=7.5g,小球落地点平均所处的位置离点O的距离根据图3所示,求:
例7若两个小球其他的条件都保持一致,就是换掉两个小球的材质,这样可以将被碰小球做平抛运动射出去的距离变的更远,根据例题6的数据,求被碰小球m1平抛运动射出去的距离ON的最大值.
解析被碰小球m1平抛运动射出去的距离ON有最大值是在两个小球完全弹性相撞的时候,根据弹性碰撞动量守恒:
参考文献:
[1]王跃军.动量守恒定律常考题型及解题策略[J].数理化解题研究,2019(31):62-65.
[2]孙长庚.动量守恒定律应用中“n”次碰撞问题探讨[J].考试周刊,2016(28):132,34.
[3]王建国.高中物理中动量守恒教学策略探析[J].武汉:新课程导学,2019(36):37.
[4]陈慧敏.基于核心素养的“动量守恒”重要概念学习进阶研究[D].武汉:华中师范大学,2019.
[5]王芸.基于核心素养的高中“动量守恒定律”单元教学设计研究[D].兰州:西北师范大学,2021.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/68624.html