SCI论文(www.lunwensci.com)
摘 要 : 在高中物理中有着比较多的公式,通过高中物理教学要求学生掌握和利用公式,灵活 使用公式解决物理问题.极限思维法是一种常见的物理解题方式,和其他物理解题方式相比,极限 思维法更加直接、快速.在高中物理解题中,引导学生利用极限思维法,对物理问题进行分析,提高 学生解题速度,将复杂困难的问题变得简单,达到事半功倍的解题效果.本文探究高中物理解题中 极限思维法应用策略.
极限思维法主要是两个量在某个空间中的变化 关系,如单调上升或者下降的函数关系,通过改变其 中的量,使得空间内变化在某个区间内达到极限.在 高中物理解题中,极限思维法有着重要的作用,借助 极限思维法有利于高中物理教学发展,提高学生解 题能力,因此,需要不断优化极限思维法,加强极限 思维法的应用.借助极限思维法解决综合性强和复 杂性问题,提高学生物理解题效率.
1 高中物理解题中极限思维法应用的重要性
高中物理解题中,极限思维法有着重要的作用, 借助有效的思维方式和解题方法,将事物变化限定 在极端内,在任意的空间或者事物中都可以进行设 置,对事物变化过程中发展规律进行分析,找出问题 解决的有效方式.极限思维法在高中解题中应用,能 够将复杂问题简单化,使得物理解题思路更加清晰, 在解题过程中,能够从极端思路出发,深入理解题目 信息,了解解题方式,简化解题步骤.总体来说,极限 思维法能够提高学生学习成绩,帮助学生掌握解题方法,得到高中学生的认可,实现学生的全面发展.
2 高中物理解题中极限思维法的应用
2.1 借助极限思维法,明确解题突破点
高中物理知识具有复杂性的特点,体现在各种 类型题目中,对于条件多、数据复杂的题目类型,解 题信息获取难度较大,面对这样的情况,借助极限思 维法,能够提高解题效果.高中物理解题中,借助极 限思维,假设任意变量,在空间内达到极限点,完成 题目解答.通过这样的方式,帮助学生找出解题思 路,剔除无用无关信息,提高学生解题效率.
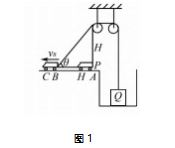
例题 如图 1 所示,在一口深井中提出一个物 体,现在采取定滑轮提取的方式,使用汽车和定滑轮 组合,在滑轮上的绳子是 PQ,物体的质量是 m,在汽 车后面挂钩位置挂上绳子 P 端,绳子的 Q 端和物体 相连.假设绳子总长度不变化,忽略绳子、定滑轮的 质量,滑轮上的摩擦力不计,当汽车开始运动时,汽 车位于 A 点,绳子处于绷直状态,两侧绳子都处于 竖直方向,定滑轮左侧绳子长度是 H,当物体提升时,汽车向左做加速运动,沿着水平方向从 A 点运 动到 C 点,途中经过 B 点.如果 A 点到 B 点的距离 也是 H,经过 B 时,汽车的速度是 VB,求解汽车从 A 点到 B 点的运动中,绳子对物体所做的功.
解析 对于此种类型题目,题目中并没有给出 到达 B 点时物体的速度,使得解题较为困难.在解 题中,学生很容易出现错误,如将汽车到达 B 点时 的速度和物体速度等同,对于这样的错误,主要是学 生没有考虑速度方向.想要解答此题目,需要明确两 者速度的关系,结合图 1 可以得出,绳子的速度和 θ 角的变化有关,θ 角则随着汽车从 A 到 B 再到 C 的 过程发生变化.作为教师,需要引导学生利用极限思 维法,利用两个理想极限值完成解题. 当 汽 车 在 A 点时,θ = 90°,绳子的速度是 0.当汽车行驶到无穷 远时,θ = 0°,绳子的速度和汽车速度相同. 因此,汽 车 A 点到无穷远的区间内,绳子速度的变化规律是 V = V车 cos90° = V车,通过这样得出汽车到 B 点的速 度,V = VB cosθ,计算出汽车到达 B 点时物体的速度. 通过极限思维法,明确解题思路,突破解题难点,轻 松求解出绳子对物体做的功.
2.2 借助极限思维法,明确解题思路
高中物理解题中,除了找出解题突破点,还需要 有着明确的解题思路,根据解题将需要的知识点联 系在一起,得到最佳的解题方式.根据这样的解题需 求,教师可以引导学生利用极限思维,将题目问题进 行极限转化,有效完成问题解答.
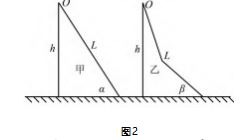
例题 如图 2 所示,在水平面上放置有甲、乙两 个斜坡装置,斜坡的坡面是光滑的,两个斜坡的高度 相同,从顶端到底端的距离是一样的,斜面甲是直 线,斜面乙则分为两个部分,如果在两个斜面顶端分别静止释放一个小球,只考虑重力做的功,请问小球在那个斜面最先到达底端? (两个小球完全相同).
个部分,分析时条件不足,常规解题方式应用较为困 难.因此,教师可以让学生利用极限思维方式,对题 目进行分析,求解小球在斜面乙上运动的时间.斜面 乙和斜面甲的不同点是斜面乙存在夹角,因此,可以 从夹角入手,两部分的夹角大小范围是 90° 到 180°. 当两个部分的夹角是 180° 时,可以对斜面甲做出分 析,当两个部分的夹角是 90° 时,小球运动可以分成 两个阶段计算.第一个阶段则是小球做自由落体运
于 90° 且小于 180°,所以小球在斜面乙上的运动时 间比斜面甲上运动的时间小,通过讨论和分析,可以 得出斜面乙上小球运动的时间短,先达到底部.
2.3 利用极限思维法,提高学生解题效率
在高中物理解题中,大部分的物理题目求解时, 对物理变量有着一定的区间限定,针对此种类型的 问题,教师可以让学生利用极限思维方式,对临界值进行推算或者假设,在对临界状态做出分析之后,形 成问题分析和解答的基准,有效提高学生解题效率.
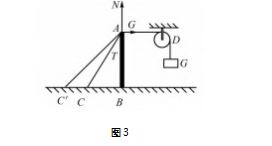
例题 如图 3 所示,图中的装置处于平衡状态, 将 AC 换成长一些的绳子 AC',杆 AB 处于竖直状态, 装置依旧处于平衡状态,那么绳子 AC'受到的张力FT 和杆 AB 受到的压力 FN 相对于原来来说,有什么 样的变化( ).
A.FT 增加,FN 减少
B.FT 、FN 都增加
C.FT 减少,FN 增加
D.FT 、FN 都减少
解析 教师可以引导学生利用极限思维法,帮 助学生找出解题思路.根据题目假设绳索 AC 和水 平面的夹角是 0°,即绳索和 AB 垂直,此时的 FT = G,FN = 0.之 后,假 设 绳 索 AC 和水平面的夹角是 90°,此时 FT = FN,且 FT 趋向无限大.根据结论对题 目进行分析,在绳索更换成 AC'后,其和水平面的夹 角逐渐变小,在夹角从 90° 到 0° 的变化中,FT 值和FN 值在逐渐变小,得出相应的结论,简化解题过程, 明确问题解题方式.对图进行分析,得出当 θ 为零 时,FT = G,FN = 0.当 θ = 90° 时,FN 很大,FT 随着 FN 的增加而增加,当 θ 减小时,FT 和 FN 也逐渐减小.
2.4 借助极限思维法,培养学生灵活思维
高中物理解题中,利用极限思维法解决计算和 分析题目外,还可以让学生利用极限思维法解决选 择,引导学生采取灵活的方式解题,保证解题效率和准确性,让学生可以更快的找出答案.
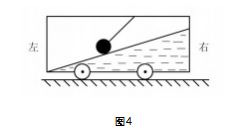
例题 一辆小车上有着一个固定的斜面,使用 细绳将一个小球连在车顶,此时小车在水平面做直 线运动,如果某个时刻,小球处于如图 4 中的状态,斜面对小球的支撑力是 FN,细绳拉力是 FT,下述有 关小球此时受力分析正确的是( ).
A.小车向左运动时,FN 的值可能是 0
B.小车向左运动时,FT 的值可能是 0
B.小车向右运动时,FN 的值不可能是 0
D 小车向右运动时,FT 的值不可能是 0
解析 根据选项中的结论,可以让学生利用极 限思维的方式思考问题,在分析 FN 时,假设斜面对 小球的支持力 FN 是 0.小球则只受到重力和拉力作 用,并且其合力是水平向右,此时小车有可能是向右 做加速运动,或者是向左做减速运动,因此,可以得 出选择 A 正确,选项 C 错误.在分析 FT 时,假设绳索 拉力 FT 是 0.小球受到重力和支持力,合力水平向 左,小车可能向左加速运动,也可能是向右减速运 动,因此,B 选项正确,D 选项错误.
2.5 利用极限思维法,快速解答疑难问题
运动学是高中物理的重要内容,主要有匀加速 直线运动、平抛运动、圆周运动等,竖直上抛运动则 是匀加速直线运动的重要内容,物体上升时,受到重 力和空气阻力影响,两者方向竖直向下,下落时,物 体重力方向向下,空气阻力向上.高中物理习题中, 结合竖直上抛内容,考查学生对匀加速直线运动的 理解,要求学生具备灵活的思维,针对问题做出分 析,利用极限思维法,提高解题效率.
例题 将某物体以 v1 的初速度竖直上抛,重新
解析 假设空气阻力无限趋向于零,那么 f 和 重力 G 的比值则无限接近零,此时 K 的值则趋向接 近于 1.此题是选择题,可以将 K = 1 带入其中,选择中结果为零的则是正确选项,正确答案是 D.
2.6 利用极限思维法,掌握解题技巧
弹簧类习题是高中物理的常见题型,能 够 考 查学生对受力知识以及能量知识的掌握程度.弹 簧形变不 同,则是会产生不同的力的效果,学 生 对问题分 析 时,难以做好准确把握. 为 了 帮 助 学 生掌握解题技巧,注重直观方式展示不同形态下 弹簧弹力 的 情 况,夯实学生基础知识,借 助 极 限 思维法的 利 用,锻炼学生思维能力,面 对 类 似 的 问题,能够采取多种解题方式,灵活利用解题技 巧,保证答案的准确性.
例题 如图 5 所示,一个轻质弹簧的两端各连 接一个小球,小球质量分别是 m1 、m2.使用一根细线 L1 将 m1 和 OO'轴相连.如果两个小球均以角速度 ω 在光滑水平面转动,两球之间距离是 L2.在某一时刻细线忽然断开,在断开的一瞬,两个球的加速度分 别是( ).
解析 得出正确的答案.根据两个小球的质量 m1 和 m2.假设 m1 无限接近 m2.在细绳断开时,弹簧 受力大小一致,方向相反,那么两个小球的加速度也 是一致的,方向也是相反的.将 m1 = m2 带入四个选 项,找出 B 选项符合要求.
2.7 利用极限思维法,检验问题结果
高中物理解题中,利用极限思维检验计算结果, 能够判断结果的准确性,提高学生解题准确率,有利于学生考试成绩的提升.
例题 在一架升降机底板上放入一个物体。升
果是错误 的,正确的答案是整个运动中,物 体 脱 离底板,物体对底板的 压 力 是 零. 因 此,利 用 极 限 思维能够检验解题结果,判 断 其 准 确 性,提 高 学 生解题准确率.
在高中物理解题中,利用极限思维法,能够达到 事半功倍 的 效 果,借助极限思维法,帮 助 学 生 理 解分析问题,寻找解题 突 破 点,明 确 解 题 思 路,掌 握解题方法和技巧,提高学生解题效率. 同 时,利 用极限思 维 法,能够检验物理解题结果,培 养 学 生严谨的 学 习 态 度,实现复杂问题简单化,提 高 学生解题效率和质量.
参考文献 :
[1] 李明.高中物理解题中极限思维法的应用 [J].数理化解题研究,2021 (15) : 2.
[2] 胡连岁.高中物理解题中极限思维法的应用探析 [J].数理化学习 (教研版) ,2019 (7) : 2.
[3] 郑建平.解析高中物理解题中极限思维法的实践 [J].中学生数理化(教与学) ,2019 (10) : 1.
[4] 席海福.如何巧用极限思维法解高中物理题 [J].数理化学习( 高一二版) ,2019(5) :45-46.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66632.html