关于无穷小的若干比较方法及应用论文

SCI论文（www.lunwensci.com）　

　　摘要：函数的极限是极限理论的一个重要组成部分，无穷小的定义与计算则是函数极限的基础．无穷小的比较问题是微积分的重要内容，为了更系统地解决此类问题，文章从无穷小比较的定义、等价无穷小定阶法、比较定阶法、泰勒公式定阶法、求导定阶法这五种方法进行了讨论，并且分别给出了对应的实例分析．灵活使用这些方法，可以做到更加有效地解决无穷小的比较问题．

　　关键词：无穷小的比较；等价无穷小；泰勒公式；定阶法

　　极限理论是高等数学的基础，函数的极限是极限理论的一个重要组成部分．极限为零的变量称为无穷小量，简称“无穷小”，在函数及数列的极限、函数的连续性、微分和积分的定义中都有无穷小的应用．然而，理解清楚无穷小的概念以及运算有一定的难度．无穷小的比较问题，不仅是高等数学的重要内容，也是历年全国硕士研究生招生考试的重要考点．本文主要针对无穷小的比较给出了几种方法，有利于读者进一步理解无穷小的含义以及更加系统地掌握此类问题的解决方法．

　　1根据定义比较无穷小

　　定义1设α及β是在同一自变量变化过程中的无穷小，且α≠0，lim也是在此变化过程中的极限．如果lim＝0，那么就说β是比α高阶的无穷小，记作β＝o(α)；

　　如果lim＝∞，那么就说β是比α低阶的无穷小；

　　如果lim＝c≠0，那么就说β与α是同阶无穷小；

　　特别地，若lim＝1，那么就说β与α是等价无穷小，记作α~β；

　　如果lim＝c≠0，k＞0，那么就说β是关于α的k阶无穷小．

　　通过定义发现，比较两个无穷小α及β，相当于求极限lim．

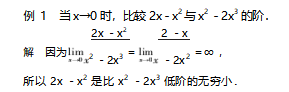
　　注1不是任意两个无穷小都可以比较，因为只有当两个无穷小量比值的极限存在或为无穷大时，才可以比较这两个无穷小．特别地，xk＋ο(xk)是x的k阶无穷小(k＞0)．类似于这个方法，对于无穷小的比较，除了可以使用定义，还可以通过确定每个无穷小的阶，然后比较阶的大小来比较两个无穷小．

　　2比较无穷小的阶

　　2．1等价无穷小定阶法

　　2．2与(x－a)k(k＞0)比较定阶法

　　2．3泰勒公式定阶法

　　2．4求导定阶法

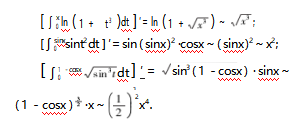
　　综上，由于∫－cosx dt的导数比其余三个函数的导数阶数高，所以∫－cosx dt是四个选项中阶数最高的，答案选D．

　　将以上四种确定无穷小的阶数的方法灵活使用，可以更加有效地处理无穷小的比较问题．

　　4结论

　　本文主要从无穷小比较的定义、等价无穷小定阶法、比较定阶法、泰勒公式定阶法、求导定阶法五种方法系统地归纳了无穷小量的比较问题，并结合实例给出了分析过程，使方法可以很好地结合实例进行应用．灵活使用这些方法，可以做到更加有效地解决无穷小的比较问题．

　　参考文献：

　　[1]同济大学应用数学系．高等数学(7版)[M]．北京：高等教育出版社，2014．

　　[2]王莉．无穷小量定阶法及其应用[J]．数学教学研究，2013，32(2)：56－60．

　　[3]华东师范大学数学系．数学分析(4版)[M]．北京：高等教育出版社，2011．

　　[4]夏滨．谈无穷小阶的比较方法[J]．理科爱好者，2014，6(2)：5－6．

　　[5]许洪范，饶维亚．非标准分析中无穷小量阶的研究[J]．长春大学学报，2000，10(6)：26－33．

　　[6]潘建辉，胡学刚，邓志颖．关于“无穷小的比较”的教学研究[J]．高等数学研究，2011，14(5)：43－46．

　　[7]方涛．关于无穷小量的几点注记[J]．上海工程技术大学学报，2013，27(3)：275－277．

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/66296.html