SCI论文(www.lunwensci.com)
摘要:高中数学蕴含很多思想,其中化归思想指将一个问题由难化易,由繁化简,由复杂化简单的思想,在解题中有着广泛地应用.高中数学教学中为提高学习者运用化归思想解题的意识以及在解题中的应用熟练程度,教师有必要做好教学经验总结,优选典型例题,做好化归思想在解题中的应用展示,给学习者带来良好的启发.
关键词:高中数学;解题;化归思想;应用
1化归思想之换元转化
换元转化是非常常用的化归方法.在遇到数学式较为复杂,不易找到数学式之间的内在联系时常使用换元转化.通过换元转化可使数学式子变得简洁,更容易构建与其他数学知识点之间的内在联系,帮助学习者尽快地找到解题思路.实践表明,换元转化的方法较多,主要分为整体换元、三角换元、均值换元等,其中前两种换元方法应用广泛,尤其在解答三角函数类的习题中可获得意想不到的效果.但需要注意部分习题并不能直接判断是否需要进行换元转化,需运用所学数学知识对已知条件进行整理,在整理过程中应具备换元转化意识.换元转化的关键在于保证换元前后取值范围的一致性,这一点应引起足够重视.
解析由|a-b|=3,可得|a|2-2a·b+|b|2=3,由2a·b+a2=0可得2|a|2+|b|2=3.令|a|=cosθ,|b|=3 sinθ,0≤θ≤.又由|a+b|2=|a|2+2a·b+|b|2=|b|2,得|a+b|=|b|.则|a+b|+|a|=|b|+|a|=3 sinθ+cosθ=sin(θ+φ),其中sinφ=3 cosφ=6.显然当sin(θ+φ)=1时,取得最大值.
2化归思想之构造转化
运用化归思想解题的方法多种多样,其中构造转化是化归思想的重要代表.构造转化指基于对相关参数关系的本质理解,运用所学数学知识构建新的逻辑关系,化陌生为熟悉,从而更好地运用所学知识解决问题.由此可知构造转化的难点在于:其一,如何通过构造将新的问题转化为熟悉的问题.解题时需认真观察所给数学式子的特点,找到共同点,为构造做准备.同时,积极联系熟悉的知识点,建立与所学数学知识的联系,完成构造.其二,构造后的处理.构造的目的在于更好地处理问题,因此,构造后应明确如何处理构造出的新关系.
解析观察a、b表达式,构造函数f(x)=ex-1-sinx,则f′(x)=ex-cosx,当x>0时,f′(x)>0,函数f(x)单调递增,即f(0.1)>f(0),所以e0.1-1-sin0.1>0,则a>b.为比较b、c的大小,构造函数g(x)=ln(x+1)-sinx,则g′(x)=-cosx=,令h(x)=1-xcosx-cosx,h′(x)=(x+1)sinx-cosx,h″(x)=2 sinx+(x+1)cosx.当0<x<时,h″(x)>0,h′(x)单调递增,即h′(x)<h′()=<0,则函数h(x)在(0,)上单调递减,则h(x)<h(0)=0,故g′(x)<0,函数g(x)在(0,)上单调递减,即g(0)>g(0.1),所以b>c.综上分析c<b<a,选择D项.
3化归思想之数形转化
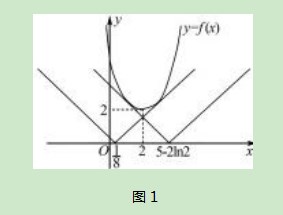
数形转化是高中数学解题中较为常用的化归方法.众所周知,数和形在本质上具有统一性,通过数形之间的转化可创造性地解决数学问题.研究发现,数形转化常被用于解答函数零点、方程根的个数以及与分段函数相关的恒成立问题.运用数形转化解题时应注意把握以下关键环节:其一,如何画出正确的函数图像.其二,如何分析出关键位置.找到图像的关键位置是解题的关键,尤其在难以直观判断出相关位置时应大胆设出参数,运用所学求出对应参数.
解析根据题意f(x)≥|x-m|恒成立可转化为函数f(x)的图像在函数y=|x-m|图像的上方.当x≤2时,f(x)=e2-x+x-1,则f′(x)=-e2-x+1,令f′(x)=0,解得x=2,当x<2时,f′(x)<0,函数f(x)单调递减.当x>2时,结合二次函数知识,不难画出函数f(x)的图像.y=|x-m|=.当y=x-m和f(x)=2x2-8x+10的图像相切时,f′(x)=4x-8=1,此时x=,求得切点坐标为(,),代入到y=x-m中可求得m=.同理当y=m-x和f(x)=e2-x+x-1的图像相切时可求得切点坐标为(2-ln2,3-ln2),此时m=5-2ln2,如图1所示,故可得出m的取值范围为[1 5-2ln2],选择C项.
4化归思想之直接转化
直接转化是解答高中数学习题时又一常用的化归方法.因高中数学习题情境以及考查的知识点不同,因此,运用直接转化解题的难度存在一定差别.部分习题运用所学知识或解题经验即可完成由陌生到熟悉的转化.而部分习题则需学习者具备较强的抽象、概括能力.为确保能运用直接转化顺利解答相关习题,一方面,要保证转化的等价性.另一方面,转化时最容易在参数取值范围上出错,尤其涉及到不等式问题时很多学习者常将不等式的符号搞错,因此,转化时应保证推理的严谨性,严格按照不等式性质进行推理.
解析函数f(x)=-1-lnxb在区间[1,e]内有唯一零点等价于方程-1-lnxb=0在区间[1,e]内有唯一实数根,即a=x+xlnxb在区间[1,e]内有唯一实数根.令g(x)=x+xlnxb,则g′(x)=1+b+blnx,令g′(x)=0,解得lnx=-b 1<-1,x<,则在[1,e]上g′(x)>0,函数g(x)单调递增,又g(1)=1,g(e)=e+be,由0≤b≤e可得1≤a≤e2+e,则2≤b+2≤e+2,2≤a+1≤e2+e+1,因此,b+2的最大值为e+2选择D项.
5化归思想之坐标转化
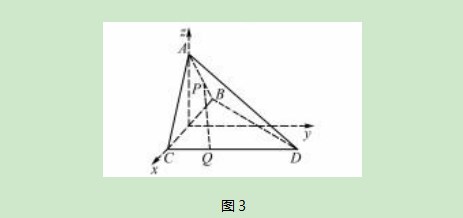
坐标转化常用于解答高中数学中较为复杂的图形类问题,尤其用于解答立体几何习题可获得显著效果.为保证转化后运算的高效性,构建合理的空间直角坐标系是关键.一般情况下应注重运用已知条件中的垂直关系构建空间直角坐标系.针对未给出垂直关系的情况,还应运用几何图形性质做出相关辅助线.另外,完成空间直角坐标系的构建后应注重运用几何图形性质、三角函数、正弦定理、余弦定理等求出相关线段长度,以确定对应点的空间坐标,并灵活运用向量运算,求出最终结果.
解析取BC的中点O,连接AO.过点O做OH∥CD.由已知条件可知,AO、OC、OH两两垂直.以O为坐标原点建立如图3所示的空间直角坐标系,易得O(0,0,0),A(0,0,1),B(-1,0,0),C(1,0,0),设点P的坐标为(s,0,t),Q的坐标为(1,m,0),其中-1≤s≤0,0≤t≤1,0≤m≤2.=(1-s,m,-t),=(1,0,-1),=(-s,0,1-t),=(1,0,1),由和共线得s=t-1,·=1-s+t,||=,||=2.又=||·||cos30°=·2·=1-s+t,整理得3 m2=4t(1-s)-(1-s)2-t2,则0≤4t(1-s)-(1-s)2-t2≤12,将s=t-1代入整理得到0≤3 s2≤1,则0≤|s|≤3故||==2|s|∈[0,],即线段PA长的取值范围为[0,].
参考文献:
[1]黄小良.例谈高中数学解题中的化归思想[J].数理化解题研究,2022(01):83-85.
[2]赵芳.浅谈化归思想在高中数学教学中的应用[J].试题与研究,2022(01):28-29.
[3]吴阳锋.高中数学解题中化归思想的有效运用[J].数学教学通讯,2020(33):52-53.
[4]何惠萍.化归思想在高中数学解题过程中的应用[J].高考,2020(14):33.
[5]厉瀛虹.化归思想在高中数学解题中的应用[J].中学数学,2019(05):47-48.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/66099.html