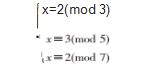SCI论文(www.lunwensci.com)
摘要:文章在阐述相关概念的基础上,首先分析了 网络空间安全专业学生培养现状,然后以中国剩余定理 课堂教学为例,对网络空间安全专业信息安全数学基础课程教学改革实践进行了论述,包括强化教学导 入,激发学习兴趣;巧用应用实例,提高学用结合能力;优化论证过程,提升数理思辨能力。
进入 21 世纪以来, 随着计算机科学技术的日益 发展,网络通信已经成为人们日常生活中不可或缺的 部分。同时,个人的身份信息、购物信息及医疗记录等 隐私信息也早就以不同的形式储存在网络中 。因此, 网络信息安全变得尤为重要 。2014 年 2 月,习近平总 书记在中央网络安全和信息化领导小组第一次会议 上的讲话中指出:“网络安全和信息化是事关国家安 全和国家发展、事关广大人民群众工作生活的重大战 略问题。”[1]在这之后,习近平总书记在不同的场合多 次提及“网络安全”。在 2018 年的全国网络安全和信 息化工作会议上,习近平总书记强调“没有网络安全 就没有国家安全”,将网络安全提升到国家安全战略 层面的高度[2] 。概言之,网络空间成为国家继陆、海、 空、天四个疆域之后的第五疆域。
新形势下,科学技术飞速发展,网络环境日新月 异,网络面临的安全挑战越来越多样化 。越来越多的 网络安全问题对个人隐私、经济、政治等造成了不同 程度的危害。比如,某购物平台存在近 12 亿条用户数 据遭泄露的问题;某出行 APP 存在严重违法违规收集 使用个人信息的问题。为应对日益复杂多变的网络环 境和日趋严峻的网络安全问题,培养我国可靠的网络 空间安全高层次人才,实施国家安全战略,国务院学 位委员会、教育部于 2015 年增设网络空间安全一级 学科,授予工学学位,下设网络空间安全专业[3] 。 网络 空间安全专业以培养具有扎实的网络空间安全理论 基础和突出的实践技术能力的专业技术人才为目标,为国家和社会输送能够从事网络空间安全研究、技术 开发及安全管理等相关工作的复合型人才。
网络空间安全属于交叉学科,涉及信息与通信工 程、数学与应用数学、统计学、计算机科学与技术、软 件工程等多个学科领域 。网络空间安全相关从业人员 需具有较高的数学素养和抽象思维能力,具有一定的 创新创造能力和全面的综合素质 。因此,网络空间安 全专业需要以未来社会需求为导向,培养具有坚定的 职业信仰、崇高的职业道德和扎实的职业技术的网络 空间安全高层次人才 。而作为网络空间安全专业的一 门主干课程,信息安全数学基础课程在网络空间安全 高层次人才培养中具有重要的地位,故本文拟以中国 剩余定理为例,对网络空间安全专业信息安全数学基 础课程教学改革实践加以论述。
一、相关概念
(一)信息安全数学基础课程
数学是所有理工科专业展开其研究内容的共同 基础 。为了适应国家和社会对网络空间安全高层次人 才的需求,网络空间安全专业的毕业生应具有扎实 的数学基础 、严谨的数学逻辑及深厚的数学素养 。 网络空间安全专业以密码学为核心内容,而密码学又 分为对称密码学和非对称密码学。其中,非对称密码学 又称公钥密码学,起源于美国密码学家迪菲和赫尔曼 在 1976 年发表的论文New directions in cryptography (《密码学的新方向》) [4] 。自此之后,公钥密码学相关理 论成为密码学的热点研究领域 。公钥密码学涉及的数学理论非常广泛,除高等数学、线性代数、概率论等普 通理工科专业课程包含的数学理论以外,网络空间安 全专业的学生还应掌握包含数论、近世代数及椭圆曲 线等相关专业数学理论。
信息安全数学基础课程是网络空间安全专业的 主干课程之一。该课程要求学生学习并掌握网络空间 安全和密码学涉及的数学理论,主要包括数论、代数 和椭圆曲线等数学理论,具体内容为整除与欧几里得 除法、不定方程、同余、同余方程、二次同余式与平方 剩余、原根与指标,以及近世代数(群与群的结构、环 论、域的结构、有限域等) 。该课程目标是要求学生掌 握网络空间安全和密码学涉及的基础数论及近世代 数相关理论,提高学生的基本数学素养,为学生以后 学习密码学相关课程打下坚实的理论基础;锻炼学生 分析问题和解决问题的能力,使其了解数学理论在现 实网络空间安全和密码学领域的应用,培养学生的信 息安全意识。
(二)中国剩余定理
1.中国剩余定理的内涵 。一次同余式组及其解法 是信息安全数学基础课程的重要组成部分,同时也是 其他高次同余式组的基础。而中国剩余定理是数论中 求解一次同余式组的重要定理,因此其是网络空间安 全专业学生必须掌握的重要定理之一 。中国剩余定理 又称孙子定理, 是中国传统文化中一颗闪亮的明珠, 凝结着中国古代数学家的智慧,是中国古代数学中具 有创造性和影响力的重要理论之一 。 中国剩余定理[5] 设 m1.m2.…,mk 是 k 个两两互素的正整数,则对任意 的整数 b1.b2.…,bk,一次同余式组
中国剩余定理相关内容最早可以追溯到 4 世纪 左右的数学专著《孙子算经》。《孙子算经》中记载了 “物不知数”,即“有物不知其数,三三数之剩二,五五 数之剩三,七七数之剩二,问物几何”。而利用现代数 学中的同余式相关理论,该题可表示为下述一次同余 式组:
对此,《孙子算经》给出了对应的解答和答案:“三 三数之剩二,置一 百四十;五五数之剩三,置六十三; 七七数之剩二,置三十 。并之,得二百三十三,以二百 十减之,即得。”“答日:二十三。”《孙子算经》中虽未 明确表示出针对一般情况的数学定理与结论,但是求 解过程已经包含了中国剩余定理的基本形式。
“物不知数”同类问题包括“韩信点兵”“秦王暗点 兵”“鬼谷算”等问题,在中国古代劳动人民中广为流 传 。南宋数学家秦九部通过对此类问题的深入研究, 在其数学专著《数书九章》中提出了大衍总数术,开创 了针对一次同余式组的系统解法, 从理论上解决了 “物不知数”问题。
1852 年,英国传教士伟烈亚力将大衍总数术引入 欧洲。大衍总数术的提出比数学家高斯在《算术探究》 中提出的关于一次同余式组的解法要早 500 多年 。 因此,在西方数学专著中,一次同余式组求解办法被 称为中国剩余定理。
2.中国剩余定理的作用。第一,南宋秦九部是中国 古代杰出数学家,在中国数学史上乃至在世界数学史 上都有着举足轻重的地位。《数书九章》是秦九部唯一 的数学著作,标志着中国古代的数学高峰,是中国古 代文化的瑰宝 。因此,学习中国剩余定理及其发展历 程, 能让学生领略中国古代先贤的杰出智慧与成就, 有助于学生树立民族自信心和自尊心,增强民族自豪 感和认同感,进一步激发学生的爱国主义情怀。
第二,中国剩余定理在公钥加密方案[6-8]、数字签 名方案[9 -10]、秘密共享方案[11-12] 和公钥叛逆者追踪方 案[13]等方面有着重要的应用 。 因此,通过对中国剩余 定理的学习, 学生能近距离地体会数学与密码学及 网络空间安全之间的联系, 真实体会到数学定理在 实际中的应用, 改变觉得数学没有实用性的错误想 法,然后进一步以点带面,提升对包括离散数学在内 的其他数学类课程的学习兴趣, 进而提高数学课堂 教学的质量 。概言之,学习中国剩余定理及其应用, 有助于学生形成敏捷的数学思辨思维, 还可进一步 培养学生的数学素养, 为学生的后续发展打下扎实 的数学基础。
第三,教师教授中国剩余定理,讲解中国剩余定 理在网络空间安全和密码学领域的实际应用例子,能 让学生领略网络空间安全学科具有的数学结构和独 特魅力,同时更真实地接触密码算法,这有助于引起 学生对网络空间安全问题的关注,激发他们对网络空 间安全相关专业知识的学习兴趣 。因此,学生学习中 国剩余定理,有助于其进一步理解现阶段网络空间安 全面临的挑战,从而帮助学生树立牢固的网络空间安 全观和国家安全观,建立主人翁意识,并引导学生更 加坚定地选择与网络空间安全相关的职业发展道路, 为后续实施国家安全战略输送高层次人才提供更加 可靠的保障。
二、网络空间安全专业学生培养现状
现阶段,网络空间安全专业学生培养中面临的问 题主要体现在以下两个方面。
(一)专业认知不够清晰,职业规划不够明确
进入 21 世纪以来, 网络和计算机相关技术飞速 发展, 且已经深入人们日常生活和工作的各个方面。 近些年来,虽然网络安全事件时有发生,并对社会造 成了巨大的损失, 但公众对网络安全的认识仍然不 足,网络安全意识淡薄。
网络空间安全作为一个新兴专业,每年第一志愿 报读的人数相对偏少 。 同时,网络空间安全专业的学 生很多都是从报考别的专业的考生中调剂过来的,这 就导致许多网络空间安全专业的学生对本专业没有 引起足够的重视 。因此,网络空间安全专业的学生普 遍缺少主人翁意识和社会责任感,且许多学生并没有 真正体会到网络空间安全专业的内涵和作用,而仅仅 是将其当成一个普通的专业。
据上所述,许多学生对网络安全面临的严峻挑战 没有引起足够的重视,对网络空间安全专业在未来国 家和社会发展中的重要地位缺乏清晰的认知 。概言 之,学生缺乏对未来从事网络空间安全相关职业的坚 定决心,且职业规划不够明确。
(二)数学基础相对薄弱,数学思维不够严谨
网络空间安全专业作为一个与数学、统计学及计 算机科学等学科领域相交叉的新兴专业,对学生的数 学基础具有极高的要求 。是否具有扎实的数学基础, 甚至影响着网络空间安全专业毕业生未来的职业发 展前景 。因此,以高等数学、线性代数、离散数学、信息 安全数学基础为主要内容的数学类课程成为网络空间安全专业的核心理论课程。
相较于其他理工科课程,数学类课程普遍具有比 较抽象、高度符号化、逻辑性和技巧性强等特点 。 因 此,学生普遍觉得数学类课程难以理解。另外,众多学 生并不理解数学对于自身发展起到的作用,也不了解 数学是其他理工科的公共基础课,片面地认为数学就 是算术和几何 。因此,很多学生认为数学类课程实用 性不高,从而导致学习兴趣不大,学习效率低下。
据上所述,包括信息安全数学基础在内的数学类 课程是网络空间安全专业的主干课程,但由于数学类 课程本身的课程特性和学生的片面理解,很多学生对 数学类课程缺乏学习的兴趣,以至于数学基础相对薄 弱,数学思维不够严谨。
笔者认为,学生专业认知不够清晰、职业规划不 够明确、数学基础相对薄弱、数学思维不够严谨均是 由于课程教学不力造成的,因此本文拟结合中国剩余 定理课堂教学,对网络空间安全专业信息安全数学基 础课程教学改革实践加以论述。
三、网络空间安全专业信息安全数学基础课程教 学改革实践
基于以上网络空间安全专业学生培养面临的问 题,可从以下三个方面进行教学改革。
(一)强化教学导入,激发学习兴趣
信息安全数学基础课程主要包含数论和近世代 数 。客观上,该课程相对比较枯燥和抽象,导致学生 对课程的学习兴趣不高 。因此,为了激发学生的学习 兴趣,教师需要结合具体的教学安排,将与教学相关 的小故事作为导入内容, 以便使学生的注意力集中 到课堂上。
中国剩余定理的产生,不仅在时间上遥遥领先于 其他国家,而且在理论与应用上有着光辉和独特的成 就。它是中国古代数学的重要理论之一。因此,在讲解 中国剩余定理的具体内容之前,教师可适当增加相关 数学史的内容,介绍中国剩余定理的名称由来和发展 历史,展示《孙子算经》和《数书九章》等中国古代数学 专著在国际数学发展过程中的地位和作用。借助这些 内容,一方面可以增强学生的民族自豪感,激发学生 学习相关内容的自信心,有助于坚定学生未来从事网 络空间安全相关工作的决心;另一方面可以帮助学生 了解古今中外的数学历史和数学文化,培养学生的数 学素养,激发学生对数学的学习兴趣,为学生更好地学习相关知识点提供必要保障。
(二)巧用应用实例,提高学用结合能力
相比于数学专业学生,网络空间安全专业学生更 加缺少系统完整的数学思维训练 。因此,在学习信息 安全数学基础课程时,特别是近世代数部分,学生往 往因为太过抽象而难以理解相关内容 。 同时,信息安 全数学基础课程虽然是一门理论课程,但网络空间安 全专业学生学习该课程的最终目的是要利用所学知 识解决网络安全的实际问题,因此在教授信息安全数 学基础课程的过程中,教师应该注重理论与应用相结 合,以网络安全相关问题作为应用实例,特别是要结 合密码学中具体的密码算法,让学生真正理解所学理 论在密码学中的具体应用。
中国剩余定理不仅在数学理论和一 次同余式组 中具有重要的理论价值, 同时在信息安全和密码学 领域,如公钥加密方案、数字签名方案、秘密共享方 案和公钥叛逆者追踪方案等具体的公钥密码算法中 也都有着重要的应用 。 因此,在开展教学活动之前, 教师应系统分析和整理与中国剩余定理相关的最新 科研成果, 了解与其相关的最新密码学方案的构造 与设计 。 同时,在教学过程中,教师应将相关密码学 方案作为中国剩余定理的实际应用进行拆解分析, 让学生真切体会中国剩余定理在实际密码学方案的 构造与设计中的应用过程, 进一步加深学生对中国 剩余定理的理解。
(三)优化论证过程,提升数理思辨能力
信息安全数学基础课程本质上是一门为了让网 络空间安全专业学生具备足够的数学基础而融合不 同数学理论的数学课程 。因此,在教授该课程时,教师 必须同时对相关理论的证明进行讲解。只有理解了证 明过程,学生才能真正明白相关定理的“来龙去脉”, 才能灵活地应用相关定理去解决实际问题。
中国剩余定理具有多种不同的证明思路和证明 方法,具体可分为构造性证明和非构造性证明两类。 其中,构造性证明能够帮助学生快速理解中国剩余 定理的内容和应用;非构造性证明能够提升学生数 学思维的严谨性, 帮助学生深入理解中国剩余定理 的本质内涵和适用范围 。因此,在讲解中国剩余定理 的过程中, 教师应当详细阐述和分析不同的证明过 程,让学生既能快速理解中国剩余定理的内容,又能 真正理解中国剩余定理的内涵 。同时,教师通过对比不同的证明方法,引导学生从不同角度思考问题,可 启迪学生的数学思维,提升学生的数学素养,为学生 学习其他数学内容提供帮助。
四、结语
在中国剩余定理课堂教学过程中,教师需要结合 其产生和发展的历史,增强学生的民族自豪感;利用 中国剩余定理在具体密码学方案中的应用实例,深化 学生对中国剩余定理具体应用的理解;通过对中国剩 余定理不同证明的分析,促使学生真正理解中国剩余 定理的内容和内涵。这些教学举措有利于促使学生提 高思想认识水平,增强学习兴趣,夯实数学基础,进而 为我国网络空间安全建设提供高层次人才,为国家安 全战略的实施添砖加瓦。
参考文献:
[1] 习近平主持召开中央网络安全和信息化领导小组第一次会议 李克强刘云山出席[EB/OL].(2014-02-27)[2023-05- 12].http://cpc. people.com.cn/big5/n/2014/0227/c64094-24486402.html.
[2] 习近平出席全国网络安全和信息化工作会议并发表重要讲 话[EB/OL].(2018-04-21)[2023-05- 12].http://military.cnr.cn/zgjq/gcdt/ 20180421/t20180421_524207152.html.
[3] 国务院学位委员会 教育部关于增设网络空间安全一级学科的 通知[EB/OL].(2015-06-11)[2023-05-12].http://www.moe.gov.cn/jyb_xxgk/ moe_1777/moe_1778/201511/t20151127_221423.html.
[4] DIFFIE W,HELLMAN M.New directions in cryptography [J].IEEE Transactions on Information Theory,1976.22(6):644-654.
[5] 陈恭亮.信息安全数学基础[M].2 版.北京:清华大学出版社,2014: 95- 109.
[6] RIVEST R L,SHAMIR A,ADLEMAN L.A method for obtaining digital signatures and public key cryptosytems[J].Communications of the ACM,1978.21(2):120- 126.
[7] 王保仓,韦永壮, 胡予濮.基于中国剩余定理的快速公钥加密算 法[J].西安电子科技大学学报(自然科学版),2008.35(3):449-454.
[8] 王会勇 , 孙爽 , 冯勇 . 基于中国剩余定理的公钥加密方案同态 性[J].计算机应用,2015.35(6):1668- 1672.
[9] 洪璇,张绪霞.基于中国剩余定理的前向安全群签名方案[J].计算 机应用研究,2020.37(9):2806-2810.
[10] 韦性佳,芦殿军.基于中国剩余定理的前向安全的聚合签名方 案[J].计算机技术与发展,2021.31(4):137- 141.
[11] 李洁平,韦性佳.基于中国剩余定理的秘密共享方案[J].通信技 术,2018.51(3):671-675.
[12] 宣妍,杨亮,高铁杠,等.基于中国剩余定理的秘密共享算法[J].南 开大学学报(自然科学版),2019(3):60-67.
[13] 杨晨,马文平,王新梅.新的基于中国剩余定理的公钥叛逆者追 踪方案[J].北京化工大学学报(自然科学版),2007.34(1):98- 101.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/64666.html