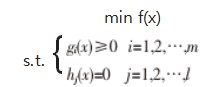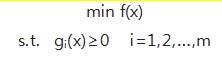SCI论文(www.lunwensci.com)
摘要:为了提高最优化理论与方法课程教学效率和质量,培育中国特色社会主义事业合格建设者和可 靠接班人,文章首先介绍了最优化理论与方法课程特点,然后分析了最优化理论与方法课程教学现状, 最后提出了最优化理论与方法课程教学改革举措,包括知识整合与系统优化、递阶引导与创新思维、直 观教学与本质揭示、学科交叉与知识融合。
关键词:最优化理论与方法课程教学,知识整合,递阶引导,直观教学
最优化理论与方法是电子信息类 、控制科学类、 管理科学类和计算数学类等专业的一 门最为基础且 重要的专业基础课程,该课程的主要内容是研究在一 定约束条件或意义下选取合理方法或技术手段,使对 象目标函数或系统达到总体最优, 从而为工程设计、 施工管理、生产运行等提出最优解决方案 。其内容广 泛应用于社会经济、信息控制、智能计算、交通运输、 国防建设、工程设计和生产管理等重要领域 。 由于该 课程理论较为抽象、知识内容有较大的跨度,所以教 师在教学过程中面临诸多挑战[1]。基于此,本文通过说 明最优化理论与方法课程的特点及分析最优化理论 与方法课程教学现状,进而对最优化理论与方法课程 教学改革举措加以论述。
一、最优化理论与方法课程特点
(一)知识交叉,要求基础扎实
最优化理论与方法课程中, 优化理论本原丰富, 优化方法众多各异 。 同时,最优化理论与方法课程在 高等数学、线性代数、大学物理、数学建模、空间矩阵、 泛函分析、程序设计等先行课程的基础上展开,所以 不仅要求学生具备较好的数学分析和解析能力,即 “算”和“用”数学能力,还需要学生具有一定的算法设 计和程序编制能力[2-3]。
(二) 内容庞杂,要求系统凝练
由于最优化理论与方法课程内容庞杂且分支众 多,同时各分支内容均有各自的数学理论知识体系和 算法(或模型),如数学分析、概率统计、矩阵论和图论 等,所以该课程涉及诸多抽象理论和算法模型,如从 离散模型到连续模型、从静态规划到动态规划、从线 性规划到非线性规划、从单目标规划到多目标规划、从无约束优化问题到有约束优化问题、从单目标规划 到多目标规划及从经典优化方法到现代优化方法等。 由于课时数有限,所以教师通常在教学过程中对优化 方法溯源讲解不够或对优化思想引导不足,更多地侧 重于讲解线性规划、非线性规划中模型构建、模型求 解、解的检验和最优解确立等求解过程,忽略了不同 数学规划模型求解方法及其与其他课程或学科领域 之间的关联性,导致学生无法从更深层次上理解和掌 握所学知识内容及其内涵本质,更无法创造性地灵活 应用所学模型概念、原理公式和理论方法分析与解决 复杂的研究课题或工程实际问题 。 因此,在设计教学 内容时,教师不仅要充分考虑其与以往所学课程知识 的自然衔接,以及课程本身知识点的系统凝练,提炼 核心观点,还要仔细斟酌与后续课程的铺垫连贯。
(三)理论抽象,要求直观形象
最优化理论与方法课程内容涉及诸多抽象理论 和概念定理,其知识点偏理论化,缺乏直观性,如最优 性理论是最优化研究的核心和算法设计的基础,该理 论较为抽象,教师在讲授相关内容时还会触及繁多的 数学知识与理论推导。学生在学习相关内容时由于缺 乏空间形象思维, 时常是被动地接受与机械地记忆, 难以很好地理解其内容本质和理论的魅力,从而会滋 生消极情绪和厌烦抵触情绪[4] 。最优化理论与方法课 程内容涉及范围广、概念定理抽象、知识理论性强,这 就要求教师在授课时应充分结合现代技术教学手段, 加强理论知识的直观性展示与图形化实现,整合课程 教学内容,丰富课程教学方式,提升课程教学效率。
二、最优化理论与方法课程教学现状
从教师视角来看,最优化理论与方法课程教学大多依然沿袭“知识传授说”模式,即以传授已有优化理 论、知识和思想及算法实现为主旨,系统地整理成课 件并传播给学生[5] 。由于该课程涉及的概念较为抽象, 教师受惯性思维影响,在教学中缺失直观形象和通俗 释疑,疏于灵活引导和有效控制,难以调动学生的学 习主观能动性,加之课堂气氛沉闷,教学互动弱化,致 使学生更多的是静听和被动地接受课程知识与内容, 最终导致课程讲授效果往往不尽如人意。
从学生视角来看,一方面,学生的基础差异较大。 对于最优化理论与方法课程教学来说,有的学生不具 备相应的数学基础和建模能力,在涉及大量且深奥的 数学理论推导学习上颇感吃力, 易产生畏难情绪,最 终失去学习兴趣 。另一方面,学生对课程地位认识不 足。当最优化理论与方法课程教师教授的知识为高度 抽象且封闭的内容时,学生没有将课程知识与学科专 业背景和课题研究方向有机结合,未能理解最优化理 论与方法课程的意义和价值, 进而难以激发学习兴 致。也就是说,在了解优化理论与模型后,对于怎样应 用所学知识科学地设计相应算法或构建合理模型,并 分析评价其算法或模型的特点, 学生会感到无所适 从,甚至难以将所学算法或模型转换为相应的计算机 语言,这不利于学生学习效率的提升。
三、最优化理论与方法课程教学改革举措
针对上文所述,笔者结合自身多年来的本科生和 研究生教学研究与实践经验, 依据控制科学与工程、 电子信息等专业培养目标,提出了基于创新性思维的 最优化理论与方法课程教学改革举措,具体如下。
(一)知识整合与系统优化
学科知识或课程知识整合是实施素质教育的主 客观要求,也是推进素质教育的必然结果 。任何学科 知识或课程知识都具有整体性、关联性、动态性和层 次性等属性,其知识类型呈现出多样化的特点,既有 定义客观事物的类别、模式和原理等概念性知识及强 调客观实际的事实性知识,也有体现方法的策略性知 识和实现过程的程序性知识等。学科知识或课程知识 整合是一种基于深度学习且超越学科界限或特点情 境,将独立化、零碎化的知识和技能进行整合,构建起 大概念、大工程观的实践活动,这种大概念、大工程观 知识具有概括性、普适性和迁移性等核心内涵 。知识 整合过程中,教师可以按照知识属性、生产实际与学 生发展需要进行新的选择、链接和转化,以促使学生 深入理解学科知识和课程知识, 实现思维水平的提升 。在设计最优化理论与方法课程教案时,教师应着 力梳理最优化概念定义、定理定律、理论方法和溯源 本质之间的内在联系和思想脉络,搭建起最优化理论 与方法课程各个知识点之间的相互关系架构,以促进 课程相关内容的有效衔接与知识点的无缝贯通[6]。
例如,无约束最优化问题知识点。
该内容的核心思想:基本送代下降算法。
知识延伸:如果为有约束最优化问题,那么为什 么其下降方向改为可行下降方向? 其数学描述怎样?
(二)递阶引导与创新思维
人的思维定式是逐渐养成而不易改变且具有两 面性的,通常会对其感知、记忆、思维和情感等心理活 动及行为活动起到积极促进或消极束缚作用。消极思 维定式表现为在认识事物的过程中囿于某种固定的 反应倾向,如优化方法中的成功案例、权威观点、标准 答案或通常做法等。在最优化理论与方法课程学习效 果上表现为思维跳不出框架,局限于传统思维和思路 策略 。思维定式束缚突破的途径主要有两个方面:一 是提升惯性思考的质量,即将更高质量的思考框架转 变为链式思考习惯;二是将有限的资源用在关键问题 的思考上,深度探究事物、方法或问题的本质,突破惯 性思维定式,提高思考效率,从而促进创新思维品质 养成。高校中,无论是本科生还是研究生,均具备一定 的逻辑推理能力和归纳总结能力,但如何有效对能力进行提升和锻炼,就需要任课教师在授课过程中精心 设计,搭建阶梯,由表及里,引领学生逐步领悟相关课 程知识的生成过程,进而自主构建知识体系[7]。
例如,最优化问题数学模型的标准化知识点。
问题 1:最优化问题数学模型一般形式通常如下:
但为什么有的参考资料给出的最优化问题数学 模型一般形式为以下形式? 两者在本质上是一致吗?
问题 2:最优化问题数学模型一般形式转化为标 准形式的通常做法是引入非负决策变量,其非负决策 变量数学描述形式有哪些?
问题 3:各非负决策变量数学描述形式有何特点? 本课程具体应用体现在哪些方面?
问题 4:针对具体实际问题如何选择相应的非负 决策变量描述形式?
(三)直观教学与本质揭示
知识是人类生产社会实践活动中智慧 、结晶和 经验的集合, 蕴含着知识产生的方法和知识内容, 是形式与内容的统一 。一 门具体的学科知识或课程 知识具有独特的视角 、思维 、对象 、内涵 、规律和话 语表达方式等 。而图表的优点是它所反映的信息简 洁、直观、丰富,便于学生理解问题 。因此,在最优化 理论与方法课程教学过程中,教师适度引入直观性 教学手段,有助于形象性地构架起抽象理论与直观 理解之间的桥梁,增进学生对相关课程基本理论的 理解,提升学生的学习效率,改善教学效果。对于最 优化理论与方法课程中的诸多问题,其灵感常源于 几何直观 。直观性教学模式是理解抽象最优化理论 和方法的有效渠道,因此教师可借助几何直观对抽 象概念、定理定律、推导证明和复杂问题进行转换, 用简明形象、直观通俗的几何语言总括性地描述其 抽象的优化思想,便于学生从全局的高度掌握最优 化理论与方法的本质特征,从而助力学生问题解决 思路的拓展。
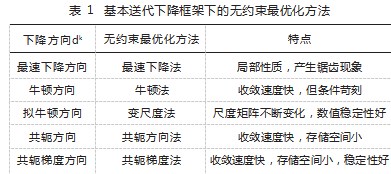
例如,无约束最优化方法总览 。利用目标函数的 解析性质来求解无约束优化问题,如何选取搜索方向 dk 是求解无约束优化问题的核心问题,搜索方向dk 的 不同选择,则构成了不同的求解算法 。基本送代下降框架下的无约束最优化方法总述如表 1 所示。
(四)学科交叉与知识融合
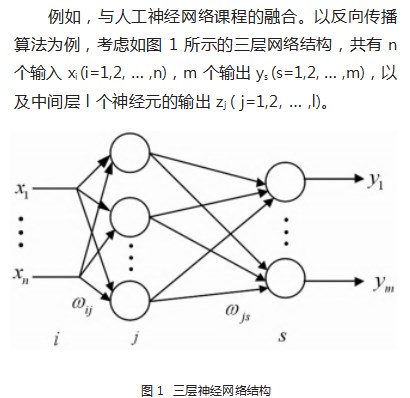
最优化理论与方法课程内容如何与时代发展、行 业需求、择业匹配和学科衔接,以及体现特色等问题 是教师在教学中需要关注和着力解决的问题 。当下人 工智能发展迅猛,新的概念、理论和方法不断推陈出 新,颠覆性技术层见叠出 。机器学习算法是人工智能 领域的核心算法, 其算法的终极目标则为最优化,即 在复杂环境与多体交互中做出最优决策。如深度学习 本质上是借助优化思想和手段,使其模型泛化误差最 小, 相 关 的 优 化 算 法 有 SGD、Momentum、AdaGrad、 Adam 及 Nadam 等 。 由此可见, 人工智能问题均可归 结于优化问题的求解或研究解的最优性,因此学习并 掌握一定的最优化理论与方法的重要性也日渐突显。 虽然最优化理论与方法是人工智能研究的基础,但该 课程理论知识和内容如何与其他课程、学科领域和实 际应用有机结合,以及体现课程特色,也是教师在推 进教学改革过程中应该重点思考的问题之一[8]。
综上所述,作为计算数学、运筹学、管理决策理论 与方法等课程的进一步延伸,最优化理论与方法课程 特点较为鲜明,其理论性较强、知识点多,这也使得该 课程教学改革是一个耗时长, 且需要不断完善的过 程。在高校致力于培养具有创新意识及创新能力的新 型人才这一大背景下, 其应该结合学生的实际特点,改革最优化理论与算法课程传统的教学模式,探索有 效的教学新途径,以提高最优化理论与算法课程的教 学质量。基于此,三年来,笔者从知识整合、系统优化、 递阶引导 、直观教学和注重学科交叉等方面开展了 多举措实践,取得了一定的成果 。通过最优化理论与 方法课程教学模式创新,将传统的“知识传授说”的 “被动学习”转变为“思维导引式”的“主动学习”,可 以将课程内容体系 、综合分析思考和工程解决能力 内化为学生个体的“大工程观”知识体系和素养[9-10]。 通过提出问题、分析问题、构建模型 、模型求解和模 型解释等环节的训练, 学生将抽象课程理论知识用 于学科前沿实际问题的解 决能力得到 了锻炼,即 “算”和“用”数学能力得到了提升,充分激发了学生 学习的积极性及学生主动学习的潜能 。此次改革取 得了丰硕的成果, 如控制科学与工程和电子信息等 学科专业的学生先后在全国大学生数学建模竞赛 、 全国大学生电子设计大赛 、全国大学生集成电路创 新创业大赛、中国智能制造挑战赛,以及中国研究生 电子设计竞赛等大赛中取得了优异成绩, 社会声誉 显著提升,生源质量明显提高 。然而最优化理论与方 法课程教学改革是一项系统工程, 尚存在诸多需进 一步厘正之处,如科学合理地创新教学评价体系等, 教师还需要进一步研究 。教学有法、教无定法,教学 改革永远在路上。
参考文献:
[1] 梁礼明,林元璋,吴健,等.“新工科”背景下地方本科院校改革发 展路径探析[J].江西理工大学学报,2017.38(6):60-64.
[2] 陈宏,邓元龙, 费跃农,等.新工科背景下混合式创新实践教学研 究[J].教育教学论坛,2021(10):33-36.
[3] 王春峰,朱铝芬.“三教”改革背景下的项目课程教学优化策略[J]. 江苏教育,2022(4):38-43.
[4] 王刚,王宜举.《最优化理论与方法》课程教学改革与实践[J].教育 进展,2020.10(6):1001- 1007.
[5] 梁礼明,吴健.主动性人格视角下电路课程创新教学研究[J].西部 素质教育,2020.6(22):1-4.
[6] 潘钊,侯培国,孟宗,等.基于情境构建培养解决复杂工程问题能 力[J]. 电气电子教学学报,2020.42(3):16-21.
[7] 徐恭贤.基于创新性思维的《最优化理论与方法》课程教学研究 与实践[J].渤海大学学报(自然科学版),2021.42(2):119- 125.
[8] 陈士涛,宋志华,许建虹.系统与优化类课程创新改革与特色核心 金课建设研究[J].工业和信息化教育,2022(1):43-47.
[9] 江桂云,罗远新,李聪波.“大工程观”视域下一流机械工程人才培 养研究与实践[J]. 中国大学教学,2020(2):37-41.
[10] 葛梦滢,杜艳玲,刘江丽.学科融合下“大工程”实践平台的探索 与实践[J].科技与创新,2021(23):10- 12.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/55257.html