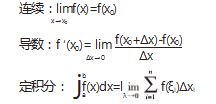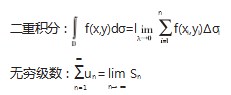SCI论文(www.lunwensci.com)
摘要:为了全面培养学生,文章从融入现实生活问题、融入数学历史、融入名人逸事、融入科学精神、融入 当代建设成就、融入数学之美六个方面论述了课程思政融入高等数学教学的策略。
关键词:课程思政,高等数学,数学历史
德国伟大的数学家、物理学家高斯盛赞“数学是科 学的皇后”。宇宙之大、粒子之微、火箭之速、化工之巧、 地球之变、生物之谜,都离不开数学 。而作为理工科专业 的公共基础课,高等数学开设时间一般在大学一年级, 基本内容主要包括函数、极限与连续,导数与微分,一元 函数积分学,微分方程,空间解析几何,多元函数极限与 微分,重积分与曲线、曲面积分,无穷级数 。对于理工科 专业的学生来说,高等数学的学习是必要的,因为只有 这样学生才能掌握必备的工具知识,进一步培养与训练 科学思维,以及自学能力;高等数学的学习是重要的,因 为它是学位课程,是后续课程学习和进一步深造的重要 基础,是一切科学研究的基础。
但就高等数学本身而言,其知识多、理论难、证明难、 计算繁,已成为制约理工科专业学生学习的一个“拦路 虎”;就学生本身而言,理工科专业部分学生的数学基础 比较薄弱,且同一专业文理兼招,学生基础相差很大[1]。 因此,在高等数学学习过程中,学生的积极性不高,缺少 动力、缺乏毅力,甚至有畏难心理 。另外,学生初入大学, 对社会环境较为陌生,对前途未来充满迷茫困惑,且他 们的世界观、人生观、价值观正处在形成的关键期,因此 教师的引导对于他们而言极其重要[2]。基于以上情况,高 校专业教育不仅要做好传道、授业、解惑的工作,还要重 视价值引领的教育意义,因此在教学过程中,高等数学 教师在传授知识的同时, 还应该充分结合数学学科特 点,深入挖掘课程蕴含的思政元素,让课程思政真正融 入教学过程[3] 。下面本文拟对课程思政融入高等数学的 路径加以探讨。
一、融入现实生活问题
数学来源于生活,又作用于生活,数学教学只有融入 学生熟知的生活情景,才能让学生有学习的兴趣 。因此, 教师应将现实生活问题融入高等数学教学, 让学生用数 学的眼光从生活中捕捉数学问题, 主动运用数学知识分 析生活现象,自主地解决生活中的实际问题。
(一)函数的极值
在讲解多元函数极值的时候,教师可以通过三个经 典问题引出多元函数极值的讨论。第一,共享单车“大战”已经拉开,其投放比例会影响收益吗?如何合理地投放共 享单车,找到它的最佳投放比例?第二,随着经济的发展, 理财会影响每个家庭的收入, 那么该怎样合理地配置理 财方案呢? 第三,航天器的外壳非常重要,那么其该如何 进行设计,才能在减轻重量的同时达到最大强度?以上这 些问题都有一个最值的概念, 其实就类似于在山脉中寻 找山峰跟山谷一样。如果想要成为最高峰,那么首先自己 必须是周围的最高峰,要想成为最低谷,那么首先自己必 须是周围区域内的最低谷,这样,一个最值的问题就转换 成了一个局部极值的问题,由此可以引出极值的概念。
首先,教师通过三个现实生活问题讲解多元函数极 值提出的应用背景及相关案例, 可以让学生了解极值的 应用,意识到数学与实际生活息息相关,从而激发学生的 学习兴趣 。其次,在讲解极值问题时,教师可以把求二元 函数极值问题抽象成在山脉中寻找山峰和山谷, 引发学 生的联想,加强学生的记忆,进而加深学生的理解。最后, 教师不仅要教学生学会求函数的极值和极值点, 同时还 要让学生感悟人生:人的一生就像连绵不断的山,谁都不 可能一帆风顺,有高峰就会有低谷,当你处于高峰时不能 自大,要懂得知足感恩,多向别人学习;跌入低谷时也不 要气馁,要沉着冷静,学会用发展的眼光看待问题,积蓄 力量,这样最终会迎来属于自己的人生[4]。
(二)函数的连续性
在讲函数的连续性时,教师可以用现实生活中的现 象举例 。 比如,温度计水银柱的高度会随着温度的改变 而连续地上升或下降,这是一种连续变化的情况。又如, 邮寄信件的邮费会随着邮件质量的增加而阶梯式地增 加, 像 20 g 以内是 0.8 元的邮费、21~30 g 是 1 元、31~ 40 g 是 1.2 元等,这是不连续变化的情况 。客观世界的 许多现象和事物都是连续变化的,如物体的运动、植物 的生长,这种现象在函数关系上的反映就是函数的连续 性。“连续”的字面意思就是不间断,反映到函数图像上 就是一条连续不断的曲线。连续函数不仅是微积分的研 究对象,而且微积分中的定理、公式、法则几乎都要求函 数具有连续性。
教师由现实生活现象引出函数的连续性概念,让抽象的概念一下子变得生动具体,可以让学生更好地理解 连续性,体会到生活中处处有数学,还能品尝到用所学 知识解释生活现象及解决实际问题的乐趣。
二、融入数学历史
数学的发展史就是一部不断创新的历史,一代一代 的数学家不囿于既定的、根深蒂固的观点,提出诘难,运 用创造性思维挣脱旧框框的束缚, 产生一次次的飞跃。 因而将数学历史融入高等数学教学,可增强数学教学的 生动性和趣味性,培养学生的科学精神、创新精神,激发 学生学习数学的兴趣。
(一)无穷小量
纵观数学史,数学理论的发展过程伴随着各种矛盾 的产生和矛盾的解决 。其实数学本身就充满矛盾,如有 限与无限的矛盾、连续与离散的矛盾等,而这些矛盾的 解决,又会反过来进一步推动数学的发展 。同时,当这些 矛盾激化到足以动摇数学基础的时候,便会爆发所谓的 “数学危机”。在数学史上,有三次比较重要的数学危机, 第一次“数学危机”是无理数的发现,古希腊时期的人们 非常崇尚整数,认为整数可以生成任何数,如有理数就 可以用两个整数的商的形式来表示,但是无理数的出现 彻底打破了这一认知,使当时的整个数学界陷入一片恐 慌,这就是第一次“数学危机”。
第二次“数学危机”是微积分的逻辑基础出现了混乱, 那么究竟发生了什么呢, 我们通过一个问题来看: “一质点做直线运动,在 t 时刻距离出发点的路程为 s=t2. 求质点在 t0 时刻的瞬时速度。”
在这个问题中,Δt 在做分母的时候不能为零, 但在 同一变化过程中说它很小,就认为零 。那时候没有极限 的定义,像这种在同一 自变量的变化过程中有时需要这 个量为零,有时又需要它不为零,这本身就是逻辑的混 乱,由此引发了数学史上第二次“数学危机”。
教师在教学中融入数学发展史的内容,如三次“数 学危机”, 既可以让学生了解极限理论在高等数学中的 重要性,加深学生对无穷小概念的理解,还可以让学生 深刻体会微积分发展历史的曲折性,从而促使学生形成 正确的世界观、掌握科学的方法论,并学习数学家不断 创新、不断探求、不断克服危机、追求真理的科学精神。
(二)数列的极限
极限是高等数学中最重要的概念之一,是微积分中 最基本的概念 。极限方法是人们从有限认识无限、从近似认识精确、从量变认识质变的数学方法。
教师对以上两个关于极限案例的讲解,不但使学生 理解了极限的概念,而且了解了有关极限方面的一些数 学史 。除此之外,教师还可以在教学的过程中加入一些 文学的色彩,借助古诗词向学生讲解极限的概念 。如徐 利治先生曾经用李白的诗句“孤帆远影碧空尽,唯见长 江天际流”描写极限的过程,这里利用了文学和数学在 极限上的契合表述极限的概念。
三、融入名人逸事
在高等数学教学中会出现很多数学家的名字,而教 师适时穿插一些数学家的小故事,能够让学生提高学习 兴趣,体会数学家刻苦钻研的精神 。因此,教师要深入挖 掘数学文化这座宝库,将名人逸事更好地融入高等数学 教学。
牛顿—莱布尼茨公式又被称为微积分的基本定理, 在讲牛顿—莱布尼茨公式时,教师可以向学生介绍关于 这个名称的由来。历史学家发现,在 1665 年的时候,牛顿 就整理出了一份微积分的草稿,但是当时他害怕遭受人 们的批评,于 1693 年才发表 。莱布尼茨独立于牛顿发明 了一套微积分学说,于 1684 年发表,是第一个发表该成 果的人。因为这个原因,在 1907 年的时候,英国数学界和 德国数学界发起了一场争论:到底谁是第一个发明微积 分的人? 有趣的是,牛顿的朋友公开发表文章表示牛顿是第一个发明微积分的人, 莱布尼茨的朋友也不甘示 弱, 发表文章表示莱布尼茨才是第一个发明微积分的 人,这件事情闹到国王那里去,差点发动战争,所幸的 是,科学界都认同两位数学家在微积分上做出的不朽贡 献,最后握手言和。
教师通过分享牛顿—莱布尼茨公式背后有趣的故 事,能够让学生感受到数学家对知识的不断追求和获得 的伟大成就,同时正向引导和激励学生,鼓励他们端正 态度,踏踏实实学习,不畏困难,永不放弃。
四、融入科学精神
科学和严谨是数学的显著特征 。高等数学是一个严 密的科学体系,其中相关的概念、定理、公式、结论都来源于实践,且经过严密的逻辑推理和论证,同时表述精 准、严格规范 。高等数学科学、严谨的学科特征对学生形 成实事求是、不轻率盲从的科学态度有着潜移默化的作 用 。因而,教师应将科学精神融入高等数学教学,让学生 养成遵章守法、爱岗敬业、诚实守信的品质,同时培养学 生求真务实的科学精神[5]。
整个探究学习经历了观察 、猜想 、求证的过程,其 中,观察需要细心、猜想需要勇气和智慧、求证需要耐心 和汗水,教师可由此培养学生观察、归纳、举一反三的能 力,使其进一步认识换元法、转化思想、数形结合思想在 数学解题中的重要作用 。 同时,教师也要告诉学生数学 是严谨的,它有自己规范的语言和表达方式,数学概念、 定理、公式、结论都要经过严格的证明才能得到,因此在 学习中要坚持实践第一 的观点,还要坚持理论和实践相 结合的原则。
(二)函数的拐点
在讲授曲线的凹凸性判定时,连续曲线 y=f(x)上凹弧 与凸弧的分界点称为曲线的拐点 。那么,曲线的拐点如 何求解呢?拐点是曲线的凹凸的分界点,因此,拐点处如 有二阶导数的话,一定等于零,当然,二阶导数也可能不存在,所以只要由这两类点把函数的定义域划分成几个 小区间,再考察每个小区间上二阶导数的符号,即可判 断曲线在各个子区间上的凹凸性,进而求出拐点 。经过 严谨的分析,求拐点的方法具体如下:首先,确定函数 y=f(x)的定义域;其次,求f ″(x),找出f ″(x)=0 的根或f ″(x) 不存在的点;最后,对于每一个这样的点 x0.若f″(x)在x0 的两侧异号,则(x0. f (x0))是 y=f(x)的拐点,否则(x0. f(x0)) 就不是拐点。
简单来说,二阶导数为零的点或不可导点都可能是 函数的拐点,因此教师在分析拐点的时候,要做到严格 规范、分析全面,不能落下任何一个可能为拐点的点,最 后在给出求拐点的方法时要简单明了、表述精准,这个 过程体现了数学的严谨性、科学性,有助于学生培养严 谨认真的科学精神。
五、融入当代建设成就
在讲解导数的概念时,教师可以用视频的方式引入 当代高铁的建设成就 。中国高铁飞速发展,不仅筑就了 祖国大地上的钢筋铁骨, 也悄然改变着人们的生活,它 时而在平直的轨道上加速行驶, 时而在弯道上蜿蜒前 行,可见让世人震撼的中国高铁是中华民族奔向伟大复 兴的“加速器”[6] 。那么,这里有两个问题值得学生深思: 高铁运动的速度每时每刻都在变化,怎么求它的瞬时速 度?当高铁驶入弯道时,为保证高铁的平稳运行,弯道的 设计会涉及求曲线的切线斜率,这个切线斜率如何求解 呢? 对此,教师可分别从物理学和几何学两个实际问题 出发,同时概括两个问题的分析和求解方法,从而抽象 出导数的概念。
教师通过对国家高铁的介绍及从物理和几何两个方 面分析归纳问题,首先,能引起学生兴趣,激发学生强烈 的爱国热情,培养学生精益求精的大国工匠精神,引导学生树立远大的理想信念,激励其积极进取、科技报国;其 次,能够让学生体会到数学的价值所在,培养其抽象概括 思维和由特殊到一般、再由一般到特殊的思维;最后,可 让学生意识到物理和数学是关系非常紧密的学科, 只有 注重相互之间的知识转化,才能取得更好的学习效果[7]。
六、融入数学之美
在高等数学中,数学知识、数学规律有着简洁美、对 称美、统一美等特征,这些数学美有助于激发学生的数 学兴趣,培养学生的数学欣赏能力 。因而教师应将数学 美融入高等数学教学,让学生感悟高等数学的形式美和 内在美,以培养学生的审美能力和数学能力。
(三)数学的统一 美
数学的统一美在高等数学中最重要的体现就是极 限,函数的连续性、函数的可导性、函数的积分,甚至一个 函数的无穷级数,都是建立在极限的基础上 。例如,
极限是研究函数的一种基本工具,极限的思想方法 贯穿高等数学的始终,因此,教师可以在讲极限的时候 把统一美有意识地演示出来,以便学生整体把握,激发 学生学习数学的兴趣。在高等数学中还有重要的概念导 数,如物理上变速直线运动的瞬时速度、几何上曲线的 切线斜率,还有电流强度、化学反应速度、经济增长率问 题等,都可以统一用导数方法解决,这些都是数学统一 美的体现。
综上所述,在高等数学中实施课程思政时,教师应找 准契合点,在教学中融入现实生活问题、数学历史、名人 逸事、科学精神、当代建设成就、数学之美,这样才会让学 生在获得知识的同时,深刻地感悟到高等数学专业知识 背后的爱国、敬业、坚持不懈、艰苦奋斗的精神,并树立正 确的世界观、人生观、价值观。
将课程思政融入高等数学教学就是要在传授知识 的过程中教会学生如何做人、如何做事 。而教师的做事 风格及工作态度会直接影响学生的价值观,因此要教育 好学生,教师还应该规范自身的日常行为,给学生做出好 的榜样[9-10]。教师只有在课上讲授高等数学知识时融入课 程思政,并在课后用自己的言行影响学生,才能实现高等 数学与课程思政的有机融合,从而为高校大学生的学习 和成长做出积极的指引 。因此,在今后的教学工作中,教 师应不断总结思政经验,努力做到真正的“教书育人”,引 导学生实现全面发展[11]。
参考文献:
[1] 何剑,胡军涛,朱四如.高等数学课程思政的目标与教法研究[J]. 当代教育实践与教学研究(电子刊),2021(13):72-73.
[2] 张苏,宋小平.高职院校高等数学教学改革的思考[J].产业与科技 论坛,2020.19(12):165-166.
[3] 潘平,邓方安.成果导向教育理念下的高等数学“课程思政”探 索[J].成才之路,2021(33):44-46.
[4] 王玉海,于卓.高等数学教学中课程思政的融入与思考[J].吉林省 教育学院学报,2021.37(9):88-91.
[5] 李迎春.从数学的特点来谈高职高等数学的重要性[J].新课程(教 师版),2011(3):162-163.
[6] 马莹,张家秀,李子煊.探究高等数学教学中的课程思政[J].创新 创业理论研究与实践,2021.4(16):44-46.
[7] 陆伟平.高等数学课程思政的思考[J].新一代,2020.25(22):41.
[8] 黎玲.课程思政融入高等数学教学中的案例设计与选取[J].现代 职业教育,2021(43):36-37.
[9] 刘明秀.高等数学课程思政认识与思考[J].科教导刊- 电子版(上 旬),2021(7):221-222.
[10] 李晓辉,张莉,程长胜,等.高等数学教学中融入课程思政的策略 研究[J].互动软件,2021(9):403.418.
[11] 田恬, 吕海侠,高汝林,等.高职高等数学课程思政的探索[J].现代 职业教育,2020(33):170-171.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/52552.html