SCI论文(www.lunwensci.com):
摘 要 :数学建模是中学数学的六大核心素养之一. 在此背景下 ,笔者研究新教材中两道有关 正六边形的向量题 , 旨在探讨新课改 ,激活新课堂 ,更好地提速增效 ,使学生的数学素养稳步提高.
关键词 :数学建模;正六边形;向量应用
1 展示正六边形的向量模型,感受数学味道
例 1 (新人教版高中数学必修第二册第一章 例 2)设 O 为正六边形 ABCDEF 的中心. (如图 1)
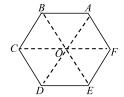
图1
(1)写出图中的共线向量 ;
(2)分别写出图中与

相等的向量.
分析 本题关键是在正六边形 ABCDEF 中找 出平行四边形. 而 ▱ABCO 的向量数式 :

. 借 用向量表示对边平行且相等 ,它起到简洁、优美的效 果 ,同时也代表一个简单图形.
解析 (1)

是共线向量 ;

是共线向量 ;

是共线向量.
→ → → →
(2)OA = CB = DO = EF;
→ → → →
OB = DC = EO = FA;
→ → → →
OC = ED = FO =AB.
例 2 (新人教版高中数学必修第二册 P60 复 习参考题 6 第 3 题) 已知六边形 ABCDEF 为正六边 形 ,

= a,

= b,分别用 a,b,表示


(如图2)

图2
分析 本题考查了不共起点的向量基底. 借用 前面例题结果 ,利用向量的平行四边形法则和三角 形法则即可.
方法 1 选用不同的基底 ,列方程组即可表示其它向量 ;
方法 2 特殊图形 ,可建立坐标系 ,用坐标法 ;
方法 3 转化为有交点的基向量 ,利用三角形法则即可.
解法 1 由图 3 可知 , 四边形 ABCO,BCDO 分别为菱形 ,其中 AC ,OB ,BD,OC 分别为对角线.

图3
设以

,为基底 ,则有

= a,
→ → →
BO = BC -AB
→ → → → →
BD = BC + BO = 2 BC -AB = b.

解法 2 因为正六边形 ABCDEF 是特殊图形 , 设边长为 2 ,则以 FC 为 x 轴 ,以 AE 为 y 轴建立如图 4 所示的平面直角坐标系 ,则 A (0 , - 3 ) ,B (2 ,- 3 ) ,C(3 ,0) ,D(2 , 3 ) ,E(0 , 3 ) ,F( - 1 ,0).

图4
则

= a = (3 , 3 ) ,

= b = (0 ,2 3 ) ,

= (2 ,0).
以下同解法 1.
解法 3 如图 5 ,因为

不是共起点的基向 量 ,设 AC ,BD 相交于点 G,则点 G 分别是 AC ,BD 的 三等分点.

图 5
以下同解法 1.
2 紧扣正六边形的向量内涵,突显核心素养
2. 1 正六边形藴含的基本图形不简单
正六边形藴含的基本图形(1)有 6 个等腰三角 形(如图 6 ) ; (2) 有 8 个等边三角形(如图 6 ,9 ) ; (3)有 6 个直角三角形(如图 7 ) ; (4) 有 6 个菱形 (如图 8) ;(5)有 3 个矩形(如图 10) ;(6)有 6 个等 腰梯形(如图 11) ;(7)正六边形的每一个角都蕴含 着 4 个 30°角 ;(8)正六边形的面积是 6 个等边三角形的面积之和.

图 6 图 7 图 8
2. 2 向量工具不简单
向量工具神通广大 ,它作为解决长度、距离、角 度、平行、垂直等问题的重要工具 ,有较好的融合度 , 与其他知识结合的试题累见不鲜. 具体如下 :
(1)利用其形的特点 ,通过向量运算的几何意义转化为平面几何的有关知识进行运算. 形如 :利用向 量的数式表示直线、三角形、平行四边形、梯形、圆等.

图 9 图 10 图 11
(2)利用其数的特点 ,通过建立坐标系 ,将向量 的有关问题转化为代数中的有关问题解决. 形如 :向 量在坐标系中推导出距离、角度、平行、垂直等公式 , 同时推导出三角形的正余弦定理、勾股定理、射影定 理等.
3 链接正六边形的高考试题,提升应用能力
例 3 (2020 年山东7) 已知 P 是边长为 2 的正 六边形 ABCDEF 内的一点 ,则

的取值范围是( ).
A. ( -2 ,6) B. ( -6 ,2)
C. ( -2 ,4) D. ( -4 ,6)
分析 本题考查了以正六边形为背景的向量数 量积运用. (1)关键在于动点 P 所在位置. 结合数量 积的射影公式及正六边形的特点 ,确定数量积分别 取得最大值、最小值时点 P 所在位置即可 ;(2)坐标 法略.
解析 画出图形如图 12 ,


,它的几何意义是

的长度与

在的投影的乘积.
观察图 12,显然 ,点 P 在 C 处时 ,

在

的投影最大 ,可得

· cos

= 6,最大值为 6.
当点 P 在点 F 处时 ,

在

的投影最小 ,


cos

= -2,最小值为 -2.
所以 ·的取值范围是( -2 ,6). 故选 A.

图 12 图 13
例 4 (2018 年上海)《九章算术》中 ,称底面为 矩形而有 一 侧棱垂直于底面的四棱锥为阳马. 设 AA1 是正六棱柱的一条侧棱 ,如图 13,若阳马以该正 六棱柱的顶点为顶点,以 AA1 为底面矩形的一边 ,则这样的阳马的个数是( ).
A. 4 B. 8 C. 12 D. 16
解析 如图 13,以 AA1 为底面矩形的另一边分 别是 AB,AC,AD,AE,AF,依题可知 ,在正六边形 AB- CDEF 内分别找以 AB 为直角边的矩形、以 AC 为直 角边的矩形、AE 为直角边的矩形、AF 为直角边的矩 形 ,不难发现,AD 为直角边的矩形是不能找到. 所以 下底面的阳马数是 8 , 同理,上底面的阳马数也一 样 ,所以阳马总数为 16. 故选 D.
例 5 (2021 年深圳一模)骑自行车是一种能 有效改善心肺功能的耐力性有氧运动 ,深受大众喜 爱 ,图 14 是某一 自行车的平面结构示意图,已知图 中的圆A(前轮) ,圆 D(后轮) 的半径为 3 , △ABE , △BEC,△ECD 均是边长为 4 的等边三角形 ,设点 P为后轮 上 的 一 点 ,则在骑动该自行车的过程中 ,

的最大值为( ).
A. 18 B. 24 C. 36 D. 48

图14
分析 本题考查以单车为背景的数量积运用. 不难联想到 ,补全后变成正六边形. 本题关键是动点 P 的位置 ,直接不能解决时 ,拆分向量

, 当且仅当 ,

与

共线同向时 ,

·

可取得最大值.

图 15
 4 加强模型变式教学,追寻有效、高效
4 加强模型变式教学,追寻有效、高效
“ 高考题常考常新”,每一年的高考题、模拟题 都会有不一样的新面孔. 如何把新面孔落实到课堂 教学活动中? 当前有一种被称为有效课堂教学 ,那 就是在某一模型的基础上 ,变更条件、编写变式题 组 ,然后进行题组化训练. 其目的是让学生熟悉考 试题型 ,在短时间内记住题型的解题方法 ,对提高学生数学能力是很有帮助的.
4. 1 变更题设条件(包括数学文化背景) ,结论不变
变式 1 (2020 年山东 7 改编) 已知 P 是五角星( 边 长 为 2 的 正 五 边 形 ABCDE ) 内 的 一 点 ,求

的取值范围是_____. (注 :cos36° =

).
变式 2 (2020 年山东 7 改编)如图 16 ,八卦是 中国古代劳动人民智慧的结晶 ,也是中国古代流传

图 16
下来的一个正八边形图案. 已知 P 是八卦图(边长 为 2 的正八边形 ABCDEFGH) 内的一点 ,求

的取值范围是_____ .
4. 2 变更题设结论 ,其它条件(包括数学文化背景) 不变
变式 3 (2021 年深圳一模改编)骑自行车是 一种能有效改善心肺功能的耐力性有氧运动 ,深受 大众喜爱 ,图 7 是某一 自行车的平面结构示意图 ,已 知图中的圆 A (前轮) , 圆 D (后轮) 的半径为 3 , △ABE , △BEC , △ECD 均是边长为 4 的等边三角形 ,设点 P 为后轮上的一点 ,则在骑动该自行车的 过程中 ,

的最大值为_____ .

图 17 图 18
变式 4 (2021 年深圳一模改编)骑自行车是 一种能有效改善心肺功能的耐力性有氧运动 ,深受 大众喜爱 , 图 18 是某一自行车的 平 面 结 构 示 意 图 ,已知图中的圆 A( 前轮) , 圆 D ( 后轮) 的半径 为 3 , △ABE , △BEC , △ECD 均是边长为 4 的等 边三角 形 ,设点 M ,P分别为前、后轮上的 一 动点 ,则在骑动该自行车的过程中 ,

的取值 范围为_____ .
5 一点感悟
新教材中的例、习题是专家们精心挑选的 ,蕴含 着丰富的数学思想和方法. 对这些具有代表性的正 六边形范例 ,充分挖掘正六边形潜在功能 ,通过一题 多解、多题一解、一题多变、推广探究等 ,把知识、素养落到实处 ,引领学生探究 ,真正达到有效、高效.
参考文献 :
[1] 林树宏 ,杨伟达. 依托数据寻找“ 变与不变”的 味道—对一道高考数学试题的赏析与教学思 考[J]. 中学数学月刊 ,2020(02) :59 -61.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/47814.html













