SCI论文(www.lunwensci.com):
摘要:本文先根据磁力线的定义式推导出两根、四根、n根无限长直线电流形成的磁力线方程,然后由柯西—黎曼方程推导出n根无限长直线电流形成的磁力线方程,最后数值模拟了几种有代表性的磁力线分布图.
关键词:无限长直线电流;磁力线方程;柯西—黎曼方程;数值模拟
1问题
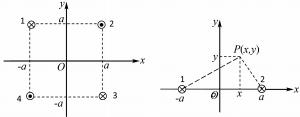
四根均通有恒定电流的长直导线1、2、3、4都垂直于x-y平面,它们与x-y平面的交点是边长为2a、中心在原点O的正方形的顶点,各导线中电流的方向已在图1中标出.已知真空磁导率为μ0.试分析空间磁力线方程是怎样的?是如何分布的?
图1图2
2磁力线方程推导
2.1两根无限长电流形成的磁力线方程
如图2所示,设两根导线的位置坐标分别是(-a,0),(a,0),电流大小分别为I1,I2,且它们的方向相同,都垂直于纸面向里.根据无限长直线电流
在周围产生的磁感应强度公式B(r)=
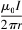
.可知x-y平面内某点p(x,y)的磁感应强度为
 若I1=I2,则磁力线方程是到两个定点(直线电流)的距离之积是一个定值.
若I1=I2,则磁力线方程是到两个定点(直线电流)的距离之积是一个定值.
若I1=-I2,则磁力线方程是到两个定点(直线电流)的距离之商是一个定值.
2.2四根直线电流形成的磁力线方程
设根四导线的位置坐标分别是(-a,a),(a,a),(a,-a),(-a,-a),电流大小分别为I1,I2,I3,I4,且它们的方向相同,都垂直于纸面向里.根据无限长直线电流在周围产生的磁感应强度公式B(r)=
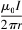 ·.可知x-y平面内某点P(x,y)的磁感应强度为
·.可知x-y平面内某点P(x,y)的磁感应强度为
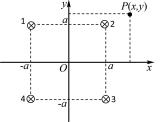
图3
 上式中C1为某一个积分常数,这个曲线簇就是本文开始问题的答案.
上式中C1为某一个积分常数,这个曲线簇就是本文开始问题的答案.
2.3n根直线电流形成的磁力线方程
不妨设互相平行的n根无限长直线电流,通过它们的电流依次为I1,I2,I3,…,In,位置坐标依次为
(x01,y01),(x02,y02),(x03,y03),…,(x0n,y0n),则它们在空间形成的磁力线方程如下:
[(y-y01)2+(x-x01)2]I1·[(y-y02)2+(x-x02)2]I2…[(y-y0n)2+(x-x0n)2]In=C,
上式中C为某一个积分常数

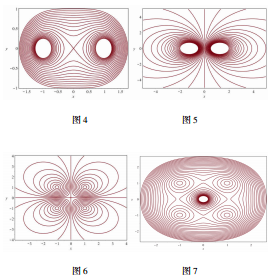 通过以上分析可以现,多根无限长通电直线形成的磁力线方程既可以用磁力线的微分方程推导,也可以由柯西—黎曼方程得到.它们形成的磁力线方程与多根无限长均匀带电直线的等势线方程具有类似性,若它们的电流大小相等、方向相同,则磁力线方程是到这些电流位置的距离的乘积是一个定值的曲线簇—卡西尼卵形曲线.限于篇幅,这里不再赘述,感兴趣的读者可以自行推证.
通过以上分析可以现,多根无限长通电直线形成的磁力线方程既可以用磁力线的微分方程推导,也可以由柯西—黎曼方程得到.它们形成的磁力线方程与多根无限长均匀带电直线的等势线方程具有类似性,若它们的电流大小相等、方向相同,则磁力线方程是到这些电流位置的距离的乘积是一个定值的曲线簇—卡西尼卵形曲线.限于篇幅,这里不再赘述,感兴趣的读者可以自行推证.
参考文献:
[1]程若磊.无限长均匀带电线与非接地带电圆柱导体系统的等势线与电场线方程[J].物理通报,2013(8):22-23.
[2]卢俊强,翟峰.平面磁场的磁感应线[J].物理与工程,2019(29):31-33.
[3]姜付锦,吴珊.论卡西尼曲线与无限长均匀带电直线系统等势线的关系[J].物理通报,2017(6):56-58.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/44213.html
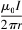 .可知x-y平面内某点p(x,y)的磁感应强度为
.可知x-y平面内某点p(x,y)的磁感应强度为
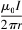 ·.可知x-y平面内某点P(x,y)的磁感应强度为
·.可知x-y平面内某点P(x,y)的磁感应强度为



