SCI论文(www.lunwensci.com):
摘 要 : 由于指数关系 aN =b 和对数关系loga b=N 是同一关系的不同表达形式,指数结构和对 数结构相互转化不会改变题目中各个量之间关系的本质属性. 本文在这一思想指导下,通过举例的 方式说明“指对互化”妙解函数导数综合问题的策略.
关键词 :指对互化;导数综合;函数综合
由于指数关系 aN =b 和对数关系loga b =N 是同一关系的不同表达形式,指数结构和对数结构相互 转化不会改变题目中各个量之间关系的本质属性. 笔者在实践中发现,如果能够利用这一特性,在解决 很多函数导数综合题目时可以起到“茅塞顿开”“豁 然明朗”的神奇效果,现将它在几种题型中的应用 举例如下 :
1 “指对互化”巧转化,大小比较不再难
例 1 (2020 年高考数学课标Ⅲ卷理科) 已知 55 <84,134 < 85 . 设 a =log5 3,b =log8 5,c =log13 8,则 ( ).
A. a < b < c
C. b < c < a
B. b < a < c
D. c < a < b
分析 因为log
5 3,log
8 5,log
13 8 ∈ ( 1 1 ),可以先比较它们与中间值的大小,要比较log5 3 与 的大小,只需比较 3 与 5 4 的大小,只需比较 34 与 53 的 大小.

解法评述 这种解法抓住了指数关系 aN =b 和 对数关系loga b=N 是同一关系的不同表达形式这一 本质属性,充分利用loga b=N⇔aN =b ⇔a =b ,利用 中间值搭台阶,将不好估值的对数式化为方便计算的指数式,思维简单巧妙触及对数概念本质,让人茅塞顿开.
2 “指对互化”妙分参,参数范围易求得
令 φ(x ) =lnx -x +1,由于 φ′(x ) =,所以 φ(x )在(0,1)上单调递增,在(1,+ ∞ )单调递减, φmax (x ) =φ(1) =0,所以 lna ≥0,所以 a ≥1 .
解法评述 由于不等式结构 aex -1 -lnx +lna ≥ 1 的复杂性,不太好分离参数,可以考虑将不等式进 行简化,变不可分参为容易分参. 这里利用“指对互 化”,将不等式两边变形为同构函数 φ [ r ( x ) ] ≥ φ[m (x ) ],再利用函数 φ(x )的单调性,转化为r (x ) ≥m (x )问题,达到巧妙简化问题的目的.
例 3 (2021 年高考浙江卷 22 题第(2)问)设 a,b 为实数,且 a > 1,函数f(x ) =ax -bx +e2 . 若对 任意 b >2e2,函数f(x )有两个不同的零点,求实数 a 的取值范围.
所以 a 的取值范围是 0 < a ≤e2 .
解法评述 本题的难点在于分离参数难度非常 困难,利用“指对互化”,构造同构函数 t=xlna,整体 换元后实现参数分离,达到简化问题的目的.
3 “指对互化”妙同构,不等证明变简单
令 r (x ) =ex (x -1) +1,有 r ′(x ) =xex .
因为 x >0,所以 r ′(x ) =xex >0.
所以 r (x )在(0,+ ∞ )上单调递增.
所以 r (x ) > r (0) =0.
所以 φ′(x ) >0.
所以 φ(x )在(0,+ ∞ )上单调递增.
故只需证明 x > ln (x +1).
即证 x-ln (x +1) >0.
令 m (x ) =x-ln (x +1),有 m ′(x ) = >0.
所以 m (x )在(0,+ ∞ )上单调递增.
所以 m (x ) > m (0) =0.
所以 x-ln (x +1) >0.
综上所述,(ex -1)ln (x +1) > x2 成立.
因为 0 < x < 1 时,r ′(x ) <0,所以 r (x )在(0,1) 上单调递减.
所以 r (x ) ≥r (1) =0.
所以 φ′(x ) ≥0.
所以 φ(x )在(0,+ ∞ )上单调递增. 故只需证明 x > ln (x +1),后同证法 1 .
解法评述 由于要证明的不等式结构(ex -1 )
·ln (x +1) > x2 过于复杂,直接构造函数证明较为 困难,需要对它进行简化,为了平衡不等式两边,这
里做了适当变形得到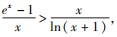 ,然后利用 “指对互 化 ” 构 造 同 构 函 数
,然后利用 “指对互 化 ” 构 造 同 构 函 数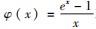 或 者
或 者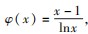 并利用其单调性成功转化为容易证明的问题.
并利用其单调性成功转化为容易证明的问题.
知名作家豆豆在《遥远的救世主》 一 书中是这 样解读“神”和“神话”的 : “神就是道,道就是规律, 规律如来,容不得你思议,规律办事的人就是神” “这个世上原本就没有神话,所谓的神话,不过是常 人的思维所不易理解的平常事”,类似地,我们可以 这样理解数学解题中的 “巧妙”与“神奇”,它不过 是按照数学知识规律办事的平常思维罢了,之所以 给我们“巧妙”与“神奇”的感觉,是因为我们对知识 本质的理解不够深刻的缘故罢了,这就要求我们深 度专研,尽可能理解知识的本质属性,并在实际解题 中不断尝试去运用它,解题就变得“巧妙”而“神奇” 起来了.
参考文献 :
[ 1 ] 刘海涛. 例谈同源法构造函数在解题中的应用 [J ] . 中学数学研究(华南师范大学版),2020 (09 ) :28-29 .
[2 ] 王淼生. 实施同构变换 构建同构函数 实现变 量分离[J ] . 中学数学杂志,2021 (07 ) :30-32 .
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/43916.html






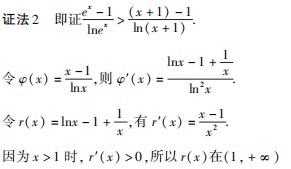
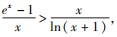 ,然后利用 “指对互 化 ” 构 造 同 构 函 数
,然后利用 “指对互 化 ” 构 造 同 构 函 数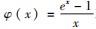 或 者
或 者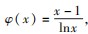 并利用其单调性成功转化为容易证明的问题.
并利用其单调性成功转化为容易证明的问题.