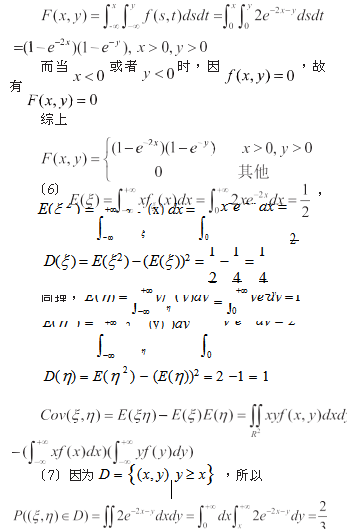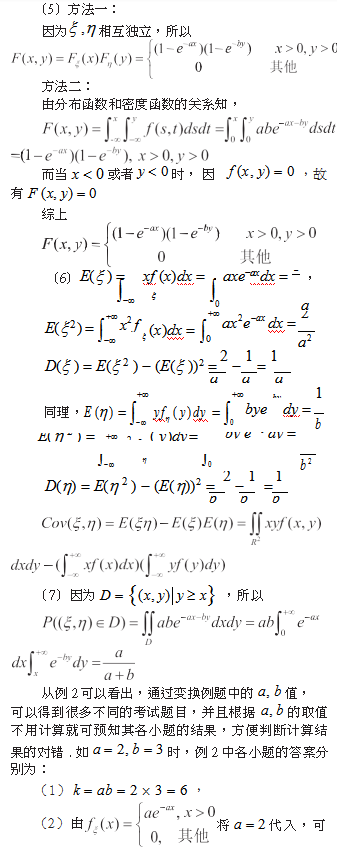典型概率论例题要举一反三论文

SCI论文（www.lunwensci.com）:

摘要：针对概率论课程的常考知识点，通过设计典型例题进行举一反三训练教学，发现如果强制性地让学生对典型例题进行达标训练，不仅有利于强化概率论基础知识的理解和掌握，使概率论的考试成绩有明显提高，而且可以让学生通过不断地挑战自己，提升学习积极性，培养良好的思维品质和创新能力，进而从更深层次上掌握相关知识，在以后的学习工作中能够灵活运用。

关键词：概率论；典型例题；举一反三

本文引用格式：马巧云，等.典型概率论例题要举一反三[J].教育现代化,2020,7(36):159-163.

Learning by Analogy for Typical Probability Example

MA Qiao-yun,LIU Tong-sheng,LV Hai-yan

(College of Information and Management Science of Henan Agricultural University,Zhengzhou Henan)

Abstract:For the common test points of probability theory,designing and training typical examplesis a good teaching way.It is found that if students are forced to train typical examples to meet the study standards,it is not only to strengthen the understanding of basic knowledge and raise the test scores,but also to encourage students challenging themselves and cultivating good learning quality,and then to master related knowledge deeply,which can be flexibly used in future learning.

Key words:Probability theory;Typical examples;Draw inferences from one instance

一 引言

概率论是研究随机现象及其规律性的一门学科[1]。围绕随机现象及其规律性的研究，需要进行随机试验并观察试验结果得到样本空间，进而对样本空间中感兴趣的结果作为随机事件研究其发生的概率，揭示随机现象的发生规律。然后，通过引入随机变量及其相关的数学描述，研究随机变量的分布及其数字特征，从而更清晰地揭示随机现象及其规律性。

随机变量的分布和数字特征是概率论的重点，不仅反映了概率论研究的根本思想，有助于培养概率思维的品质，而且是概率论教学大纲和考试大纲的基本要求[2]。近年来的教学实践表明，如果老师能找准典型例题，强制性地让学生对典型例题进行达标训练，不仅可以有效地掌握概率论的基本知识，使考生的概率论答卷明显得以改善，而且对于学生后续的学习和工作有极大的促进作用。

文中呈现的例题涉及随机变量的主要知识点和考点，包括：（1）密度函数的定义和性质（2）分布函数的定义和性质（3）联合分布和边缘分布（4）独立与相关性（5）数字特征（6）随机变量表达事件概率的计算等，基本可以涵盖随机变量及分布相关的主要知识点[3]，可实现对概率论基础知识掌握程度的检测。在例题呈现基础上通过对其进行深入剖析，揭示了例题本身的典型特征，探究了典型例题举一反三的教学过程及其作用。

二 例题呈现






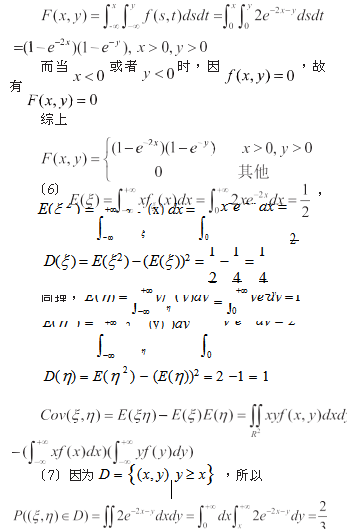三 例题剖析

（一）契合大纲，涵盖知识点多

本道例题包含七个小问题，涵盖了随机变量的概率密度和分布函数、多维随机变量的联合分布与边缘分布等基本概念，以及随机变量的数字特征和与随机变量表示相关事件的概率的计算，还有随机变量间独立性的判断和证明、独立与相关的关系等[4]。而这些知识点的考查广泛出现在概率论课程的考试及研究生招生考试中的概率论部分。从教学大纲和考研大纲来看，分布函数的概念和性质，离散型和连续型的随机变量及其分布，二维随机变量的联合分布、边缘分布和条件分布，随机变量的独立性和不相关性，以及随机变量的数学期望、方差等数字特征，都是教学的重点也是考试的重点。

（二）规律性强，方便举一反三

本道例题不仅解题方法和过程有很强的代表性，而且解的结果也有典型的规律性。可推广到一般情况见例2。





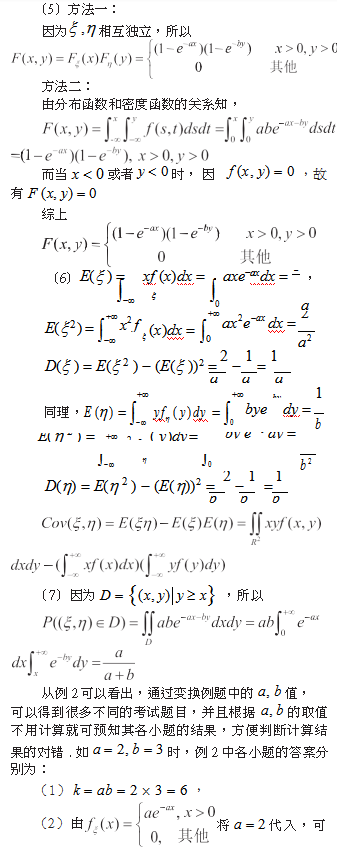
这样，非常方便地通过修改数据,例如a2,b3，或者a5,b2等进行举一反三训练，不仅有利于对概率论基本知识点的掌握，也有利于学生在训练中找到成就感，不断挑战自己，进而提高学生学习数学的积极性和主动性。

（三）具有可拓展性，可启发思维

本道例题还可拓展到离散情况，如可将本题拓展为如下的例3。这样不仅可以有效复习相关知识点，而且可以通过类比思考，启迪思维。因离散型随机变量及其分布比较具体，相对容易求解，例3便不再给出详解。



（四）具有广泛的应用性

例1给出了一类典型的连续型随机变量的分布规律，即指数分布。指数分布广泛用于表示独立随机事件之间发生的时间间隔的概率问题，比如旅客进机场的时间间隔，手机来电的时间间隔，网站访问的时间间隔等。指数分布也是一种常见的寿命分布，但因其具有的无记忆性，违背了机械零件的损伤累积和老化规律，虽然不能作为机械零件功能参数的分布规律，但可以近似地作为高可靠性的复杂部件、机器或系统的失效分布模型，特别是在部件或机器的整机试验中有着广泛的应用。在寿命分布和可靠性研究[5]中，也经常会用到类似的指数分布。

四 教法过程

例题是数学学习过程的重要部分，数学知识的掌握、能力的提高、思想方法的形成、综合素质的培养都需要通过例题的教学来实现[6]。例题不仅涵盖了知识信息，而且可以激发学生学数学的兴趣，并方便监测学生的学习效果[7]。因此合理地设计例题教学过程和方法是决定数学教学效果的关键环节。

遵循由易到难、演练再现、举一反三的原则，可以很好地达到掌握基本知识、培养思维品质和能力的目的。

（一） 由易到难

例中涉及的各个知识点在各章节学习过程中应当作为重点加强举一反三训练，在学习完概率论全部课程时，首先将例1作为综合练习题加以呈现，并围绕该例题强化密度函数、分布函数、联合分布和边缘分布、独立性等基本知识点，引导同学思考将这类问题一般化为例2。最后再通过对a,b具体化，进行举一反三训练。如a2,b3，或者a5,b2等，为了避免有同学因恐惧二重积分而放弃对本类典型题的练习，也可先从离散情形的例3
开展举一反三训练，在熟练掌握例3解题过程和熟悉基本概念的基础上，补授二重积分要点，引导学生对比完成例1的练习，再推广到例2。

（二）演练再现

数学学习离不开解题，因为“问题”是数学学习的心脏[8]。演练再现将少数学生的上台演板和多数同学的台下练习相结合，老师既要关注台上，又要关注台下，及时发现问题。这种演练再现的过程不但可以展示知识生成，也有助于及时发现并纠正学生解题中的错误，是弥补知识漏洞、强化学生认知的重要途经。通过演练和讲评，可加深学生对基本概念的理解和对基础知识的掌握，并通过课堂测验来检验学生的学习效果。

（三）举一反三

针对课堂测验成绩不好的同学，要求其对该类题型通过不断调整题目中的参数a,b取值，进行举一反三强化训练，并由老师或者指定同学作为负责人进行监督，强制这些学生对本例题进行达标训练，以致让学生达到可以为自己出题，并做出正确结果，并使学生在构造习题的过程中学会创新，勤于探索，达到培养学生创新能力的目的。

五结语

典型例题因其能较好地概括新知识的生成和发展，是巩固基础知识、启迪创造性思维的重要工具，而练习则是数学知识生成和发展的根基。因此对典型例题进行举一反三训练，不仅可以加深学生对基本概念的理解和对基础知识的掌握，及时发现并纠正学习中的错误，而且有助于培养学生的创新能力和良好的思维品质。在今后的数学教学中希望我们的老师能根据学生的认知现状，在认真研读课本和大纲的基础上，精心创设和优选典型例题，借助典型例题在教学过程中的开启功能，既要有重点讲解，又要有举一反三训练，以有效促进学生创造性思维的发展，使学生能领略到学习数学的价值。

参考文献

[1]盛骤，谢式千，潘承毅，等.概率论与数理统计(第四版)[M].北京：高等教育出版社，2008：1-2.
[2]教育部考试中心.全国硕士研究生招生考试数学考试大纲[M].北京：高等教育出版社，2019：11-12.
[3]陈振，郝新生，王建军.概率论与数理统计[M].北京：中国农业出版社，2019：56-123.
[4]刘慧君.高等学校概率论教学改革的探索与实践研究[J].数学学习与研究，2018（11）：39.
[5]刘勇，冯付勇.可靠性评估——概念和模型及案例研究[M].北京：国防工业出版社，2018：3-5.
[6]何金明，杨柳.数学例题教学研究[J].教学与管理，2016,(1):40-42.
[7]庄中文.探究高等数学教学质量提升的策略[J].教育现代化，2019，6（39）：159-161.
[8]Halmos P R，弥静．数学的心脏[J]．数学通报，1982，（4）：27-30．

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/31112.html