SCI论文(www.lunwensci.com):
摘要:对于理工科高等院校的部分理工类专业,《复变函数与积分变换》作为专业基础必修课,对学生的创新能力和所学知识的应用能力的培养及提升学生的数学素养等方面有着不可替代的作用。本文从这门课程的自身特点出发,剖析了该课程教学中所存在的问题,并在此基础上,围绕“应用型人才和创新性人才”培养的需要,基于本人多年的教学实践与经验,针对《复变函数与积分变换》课程的教学改革进行探讨,提出了一系列的改进措施。
关键词:脉冲函数;Fourier变换;Laplace变换
本文引用格式:孔芳弟.《复变函数与积分变换》课程的教学改革探讨[J].教育现代化,2020,7(51):72-74.
Discussion on the Teaching Reform of Complex Variable Function and Integral Transformation
KONG Fang-di
(School of Science of Lanzhou University of Technology,Lanzhou Gansu)
Abstract:As a basic compulsory course for science and engineering students,the course of Complex Variable Function and Integral Transformation plays an irreplaceable role in cultivating students;abstract thinking ability,logical reasoning ability and ability to analyze and solve problems by using the learned knowledge comprehensively.In this paper,we analyze the characteristics of the course itself,and point out the existing problems in the course when we are teaching.And on this basis,in order to cultivate“applied talents and innovative talents”,combined with teaching experience and practice,we discuss the Complex Variable Function and Integral Transformation course teaching reform and put forward a series of improving measures.
Key words:Pulse function;Fourier transform;Laplace transform
一 引言
随着科技和经济的高速发展,社会所需求的人才变得多样化,这为高等学校的人才培养带来了机遇和挑战。高等学校的教育必须立足于为我国社会经济的发展提供全面的服务,为我国的科技创新提供强有力的支撑,因此人才的培养模式也应逐步由传统的传授理论知识为主向应用型人才和创新型人才的培养模式转变。《复变函数与积分变换》作为理工科高校部分理工类专业学生的专业基础课,在培养学生的创新能力和所学知识的应用能力以及提升学生的数学素养等方面发挥着不可替代的作用。近几年来,相关工作者对该课程的教学内容、方法、手段一直十分关注。关于《复变函数与积分变换》课程的教学改革涌现出不少新的思想、方法和模式,参见文献[1-7],这些研究成果为更好地开展该课程的教学活动提供了许多帮助,同时也引发了更多的关注和思考。本文从课程的自身的特点出发,剖析了该课程教学中所存在的问题,并在此基础上,围绕“应用型人才和创新性人才”培养的需要,基于本人多年的教学实践与经验,针对《复变函数与积分变换》课程的教学改革进行探讨,提出了一系列的改进措施。
二课程的特点
我校部分专业的培养计划中,该课程作为基础理论课,是后续专业课程必不可少的数学理论基础。该课程由两部分组成:复变函数与积分变换,复变函数是理论基础,积分变换是理论应用,两者关系密切。该课程具有其自身的特点。
首先,具有抽象性。该课程的理论性很强,内容抽象、知识之间联系紧密,综合性强。虽然很多知识点与《高等数学》中所学的类似,例如:复变函数的极限,表面上定义形式与高等数学中的一元函数的极限类似,实质上却与二元函数的极限类似,但又有不同之处。与《高等数学》相比较,该课程的数学理论更具有深度,知识更加复杂,理解更有难度。
其次,具有实用性。该课程的知识内容产生于理论和实际需要,很多知识点都有其几何背景和实际应用背景,尤其是积分变换具有很强的工程应用背景。该课程是部分理工类专业学生后续诸多专业课程的理论基础课,例如:脉冲函数和单位阶跃函数在很多专业课程中都会涉及到。
再次,课程的知识体系有其本身的系统性。该课程中复变函数部分的知识作为《高等数学》课程的拓展内容,有许多类似之处,但有自成体系,而且每一部分知识又有其独特的处理方法。
最后,具有很强的思想性。不管是该课程的知识内容安排,还是知识结构体系都具有严密的逻辑性。
三教学过程中存在的问题
该课程的教学过程中也存在着诸多问题,简单列举如下。
(一)课时少,教学内容多,教学任务重
目前大部分高校对于该课程缺乏足够的重视,培养计划中只有48课时,为了节省课时,授课教师并不能深入系统地讲解课程的大部分内容,使得学生对所学知识理解不够透彻,无法构建完整的知识体系。由于课时紧张很容易忽视所授知识的应用背景,从而也忽略了基本概念和原理的实用性,使学生觉得内容枯燥,学而无用。
(二)重理论,轻应用
该课程的数学推导非常严密,体系十分完整。作为数学类课程,授课教师更加注重知识体系的理论完整性,不由自主地忽视了与后续专业课程的衔接,使得学生对知识的学习只是停留在理论层面,以至于在后继课程和实际应用中遇到相关的知识手足无措。
(三)学生的课堂参与度较低,思维培养成效并不好
该课程的授课主要还是采用传统的讲授式教学,学生的学习状态还是停留在课堂上听老师讲课、做笔记,考试前背公式、刷题,并没有起到很好的培养思维方式的效果。
(四) 学生的畏难情绪严重
该课程的基础课程是《高等数学》,尤其是高数下册的学习已经使得很多学生对数学类课程的学习有了严重的惧怕心理,而《复变函数与积分变换》课程具体用到的又是高数下册的许多知识点,大部分学生对这些知识的掌握并不是很理想,从一开始就抱着学不懂的心态,这使得该课程的学习就显得更加困难。
四 教学改进措施
针对上述课程的自身特点和教学中存在的问题,结合本人多年的教学实践和经验,从教学目标、教学思想和方法、课堂教学过程以及考核方式等方面给出了一系列的改进措施。具体而言,可以从以下几个方面入手。
(一) 设定教学目标,优化教学内容
在设定该课程的教学目标时,不但要注重课堂教学目标,而且还要关注该课程的教学使学生收获什么。依据设定的教学目标,结合该课程的抽象性和系统性,优化和调整课程内容,针对数学理论很强的知识点,尽量避免过多的理论推导和证明,通过简化推导证明,强化思想渗透,使学生掌握主要的思想和方法,从而训练学生的数学思维模式,以备在后续的学习和实践中使用。
(二)教学思想与方法的改进
1.由于《复变函数与积分变换》课程中的复变函数理论是《高等数学》的延续与拓展,所以知识内容有许多类似之处。在教学过程中引导学生类比相似的知识点,分析它们的相同之处与区别,尤其关注不同之处。比如:复变函数的极限和连续与高等数学中相应内容的类比,从定义形式来看,复变函数的极限lim f(z)A与一元函数的极限lim f(x)a定义完全相同,但是当数域从实数域扩充到复数域时,自变量的变化由xx0改变为zz0,故此,从本质上来看,与二元实函数的极限相似,但又不同,因为zz0在复平面上类似于于二元函数的极限中的自变量的情形,但是函数值f(z)A也是在复平面上,与二元函数的极限又不完全同。复变函数的连续与一元函数的连续的类比思想学习同于极限的学习。因此在教学过程,设法让学生通过具体知识点的类比真正地理解所学的知识。
2.在该课程的授课过程,不但要类比相似的知识点,而且还要引导学生将复变函数中的新知识转化为高等数学中已学的知识,从而降低新知识的难度,使学生更容易掌握新学的知识,同时也可以整合所学的知识,一举两得。接下来还是以复变函数的极限和连续为例来分析。复变函数的极限
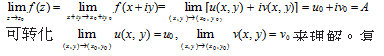
变函数的连续也可以做类似的转化。这样的转化思想贯穿于该课程的整个教学与学习过程中。在教学过程中,授课教师对可以转化的知识点,提前布置为预习作业,鼓励学生独立自主地完成知识的转化,这有助于训练学生已学知识的综合应用能力。
3.比较法教学与学习。《复变函数与积分变换》课程自成体系,而且每一部分知识又有其独特之处。结合上述讨论,在该课程的授课过程不断的对知识点进行横向和纵向比较,从而提升学生的逻辑思维能力和推理能力以及已学知识的应用能力。
(三) 与后续专业课程加强融合
该课程的学习目的主要是为后续专业课程提供数学理论基础。授课教师应根据不同专业对知识的不同需求,全面了解后续专业课程所用到的知识,在教学过程中有针对性地进行教学。例如:对于工科的学生而言,更多的时候需要掌握的是脉冲函数在信号的分解中的应用,而不是它的具体定义及理论分析,所以在教学过程中,简化理论介绍,重点讲解这个函数的性质和应用,从而使学生在后续学习过程中碰到这个函数就知道该如何去用。这样一方面降低了从数学角度理解函数的难度,另一方面也解决了学生所学数学理论知识在专业课程中的应用问题。在Fourier变换和Laplace变换的教学过程中,也一定要着重介绍它们良好的性质及其应用,并详细说明这些知识在后续专业课程学习中所起的作用。(四) 按照学生的专业,设计不同的教学案例在与后续专业课程加强融合的基础上,授课教师适当的设计与学生专业相匹配的教学案例,为专业课程的学习打好数学理论基础。例如:对于电气工程及其自动化的学生而言,根据相关知识尽可能多的设计一些与信号处理相关的案例,通过详细分析所选择的案例,学生可以体会到数学知识在专业课程中是如何应用的,从而破除数学基础理论知识学而无用错误思想。
(五)分组讨论汇报式教学
为了培养学生的团队合作精神,采取课堂外分组讨论的教学方式。选择一些知识点作为讨论讲解的专题,目前我们展开的讨论专题共有两个内容:初等函数和复积分与第二型曲线积分(对坐标的曲线积分)的联系和区别。每次专题在本章开始的时候就先预留给学生,完成时间为1—2周。在这1—2周的时间里,学生们可进行课外的探讨、交流、查阅资料,形成团队对该专题的认识和总结。专题初等函数是每个团队派一人在课堂进行讲解,而专题复积分与第二型曲线积分(对坐标的曲线积分)的联系和区别要求每人上交一份小结报告。这一教学方法,激励学生主动学习,提高学生的积极参与性,也增强了同学们的合作与交流,并且通过查阅整理资料,学生可以整合所学的知识,为将来应用这些知识做好储备。
(六) 既教书又育人,立德树人
我国高校课程教学改革正在推行“课程思政”教学改革。授课教师可以将思政教育融入《复变函数与积分变换》课程的授课过程中,充分将该课程的授课与思想政治教育结合起来,同时也要挖掘该课程所蕴含的思政元素,努力做到既教书也育人,培养出既有专业素养,又具有美好道德情操的应用型人才和创新型人才。
(七) 考核方式改革
我们采取最终考核成绩为平时考核和期末考核的综合成绩的考核方式。平时考核主要包括:作业、课堂汇报、平时课堂表现和专题及结课报告,结课报告为同学们需要结合自己的专业,深入剖析该课程所学知识与他们的专业课程的联系,写一份报告,在授课的最后一周提交。平时考核成绩共计100分,占总评成绩30%,其中课堂汇报中表现优异的个人及其所在小组的其他成员都会有不同层次的加分。期末考核是指课程教学结束后的期末考试,考核成绩共计100分,占总评成绩70%。这样的考核方式注重学生的平时学习状态,有助于学生重视平时的学习,把功夫下在平时的学习过程中,弥补了期末考试前,学生在短时间内通过冲刺复习,也可以获到高分的弊端。
五 总结
本文从《复变函数与积分变换》课程的自身特点出发,对该课程教学中存在的问题加以分析讨论,提出了改进措施。在该课程的教学过程中授课教师可以借鉴上述的改进措施,为将学生培养成为社会所需要的应用型人才和创新性人才添砖加瓦。
参考文献
[1]沈纪萍.《复变函数与积分变换》课程的教学改革与探索[J].中国科教创新导刊,2014(7):32-33.
[2]庞慧慧,陈静.《复变函数与积分变换》课程“点线面体”式教学新模式的探讨[J].大学数学,2019,35(5):50-54.
[3]刘显全.复变函数教学法探讨[J].大学数学,2012,28(2):155-158.
[4]王科,王颖,张霆.“复变函数与积分变换”教学改革思考[J].成都工业学院学报,2019,22(1):102-103+108.
[5]王莉,杨峥,王诗云,等.《复变函数与积分变换》课程教学方式的改革与探索[J].教育进展,2018,8(3):237-240.
[6]徐兴波.浅谈基于混合式教学的复变函数与积分变换教学改革[J].教育现代化,2018,5(01):89-91+104.
[7]高艳辉.复变函数与积分变换课程在几门工科类专业课中的应用[J].教育现代化,2019,6(26):130-132.
[8]华中科技大学数学与统计学院.李红,谢松法.复变函数与积分变换(第四版)[M].北京:高等教育出版社,2013.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/30753.html