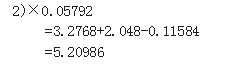概率统计方法的应用案例研究论文

SCI论文（www.lunwensci.com）:

摘要：概率论与数理统计是一门重要的应用学科，在经济管理，质量管理，军事战争都有重要的应用。其中的全概率公式，Bayes公式，大数定律，中心极限定理及常用的分布，在日常生活中都有很重要的应用，本文首先简要介绍概率统计理论知识，然后通过几个具体的实例介绍概率统计知识在生产生活中的应用，解决生产生活中的一些实际问题。

关键词：全概率公式；中心极限定理；大数定律正态分布

本文引用格式：姜丽颖,张国林.概率统计方法的应用案例研究[J].教育现代化,2019,6(81):275-276+278.

概率论与数理统计发展历史悠久，最初是由分赌本问题所产生，经过多年来的发展，概率论的研究由早期的古典概型计算，逐步发展到应用分析学的方法来解决概率的问题。而数理统计的研究则由初期的样本，总体的选取，平均值、方差的统计发展为抽样分布的研究，大数据的处理。

概率论与数理统计这一学科主要研究随机现象的统计规律，在古典概型的问题中，主要研究摸球问题，随机取数问题，分房问题。在更复杂的问题中，引入随机变量来研究随机现象结果的规律，例如，可以求出抽取产品次品件数的分布列，顾客在服务窗口等待服务的时间等问题，随机变量也因此分为离散型随机变量和连续型随机变量。常见的离散型随机变量中，0-1分布、二项分布、泊松分布以及泊松定理，可以解决类似于某一人群中，感染病的传播问题；在常用连续分布中，利用正态分布，解决产品尺寸设计实际问题，工厂每件商品的利润的问题。随机变量的数字特征是反映随机变量取值规律的代表性数字，由数字特征可以直观的反映出随机变量的平均值，偏离波动情况，而两个随机变量协方差及相关系数可以反映两个变量之间的相互关系。大数定律中心极限定理可以解决大量试验结果近似服务从正态分布的问题、参数估计及假设检验的内容可以确定分布已知、参数未知的问题中参数的确定[1-2]。

一 提高消防系统的安全性应用

（一）事件的独立性

设A，B是两个随机事件，若P(A)>0，可以定义PB A。一般的，A的发生对B的发生的概率是有影响的，这时PB APB，只有在这种影响不存在时，才

（二）利用随机事件的独立性可以解决报警器并联，提升系统可靠性的问题

例如：在消防安全中，经常通过连接报警器，保障在发生火情时，向人们报警，当连入的报警器感应到火情，开关自动闭合，发出报警，设开关的可靠性0.96，为提高可靠性，可以通过并联多个开关，即至少有一个开关闭合，系统就发出报警[3]。问题:

若两个开关并联，则系统可靠性（即系统闭合概率）是多少？

若系统的可靠性应达到0.9999以上，则至少需要多少个这种开关并联？（注：各开关的闭合相互独立）

解：Ai表示第个开门闭合。i=1,2……n则P(Ai)=0.96。

两开关并联，系统闭合的概率：





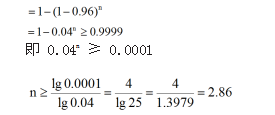
∴至少需要3个开关并联

说明：通过这个实例可知，并联开关提升了消防系统的可靠性。

二 通过计算数学期望值，掌握未来所获收益情况

（一）数学期望的计算，对经济活动的重要意义

在经济活动中，收益的大小是每个参与者关注的主要内容，而生产的每一件产品，受多种因素的影响，可能出现不同的结果，而不同结果带来收益自然不同。利用数学期望，则可以快速预知，可能收益的多少[4]。

利用期望和方差对投资管理中的相关决策进行集中分析需要关注如下几方面问题。要想提高经济金融问题处理水平，相关人员就要整合概率统计的相关内容，确保具体问题具体分析。最重要的是，在经济管理决策制定之前，因其本身存在很多不确定因素，为保证决策工作的科学高效，规避其风险性，就要建立健全完整的数据处理和运维监督机制，保证在正确、科学的原则下，完善最小成本管理工作，确保提高项目的安全效果及收益，也为后续目标管理工作的系统化升级奠定基础[5]。

（二）利用数学期望，确定预期收益的实例研究

设一部机器在一天内发生故障的概率为0.2，机器发生故障时全天停工。若一周5个工作日无故障，可获利润10万元；发生一次故障仍能获利5万元；发生两次故障所获利润0元；发生三次或三次以上故障就要亏损2万元，求一周内期望利润是多少？




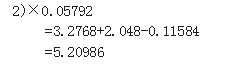三 汽车装载超重问题

现代社会，物流运输业飞速发展，汽载装载是否超重是物流中重要的一个问题，根据一批货物质量的均值，及方差，结合中心极限定理，可以方便判断超重的概率。



在一般情况下，随机变量受各种随机因素影响，可以理解为由多个相互独立的随机变量相互作用的结果。比如，参加一次比赛，是否获得成功，是由许多方面的因素所决定的。一次试验结果的测量误差是由仪器、温度、湿度、风速等多方面误差累积而成。中心极限定理的含义是，当多种随机误差共同对一个随机变量产生影响而导致其随机取值时，这个变量的分布就会近似地服从正态分布。中心极限定理是概率论的重要内容，也是数理统计学的理论基础。在现实生活中，一些受多种因素影响的随机变量的问题，都可以使用中心极限定理来解决。

2.中心极限定理的应用案例分析：设各零件的质量都是随机变量，它们互相独立，且服从相同的分布，其数学期望为0.5kg，均方差为0.1kg，问5000个零件的总质量超过2510kg的概率是多少？



总之，概率论与数理统计在生产生活的各个方向都有着广泛的应用，随着大数据时代的到来，其理论及方法也必将发挥更大的作用。

参考文献

[1]何林海.经济金融问题中的概率统计及应用[J].江西电力职业技术学院学报,2018(7):13-14.
[2]石磊.概率统计在经济中的应用[J].现代国企研究，2018（2）:75+77.
[3]范国兵.财经院校概率统计课堂教学改革的实践与研究[J].山东农业工程学院学报,2017(4):12-13.
[4]何志华.经济分析中概率与数理统计的应用评价[J].现代营销(下旬刊),2017(1):35.
[5]孔庆军.浅谈概率统计教学中的数学建模思想[J].教育现代化,2017,4(29):123-124.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！
文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/jiaoyulunwen/29413.html