【摘要】目前关于多车场绿色车辆路径问题的研究相对较少,文中在该问题的基础上,进一步考虑了现实配送过程中的时变路网特性,研究了时变路网下考虑软时间窗的多车场绿色车辆路径问题。首先,建立了以配送总成本最小为优化目标的数学模型,其中,配送总成本包括碳排放成本、货损成本、时间窗惩罚成本等五方面,同时在模型中考虑了实际配送过程中的车辆时变速度,以及车辆不得超过最大行驶距离等约束条件。随后,提出了改进遗传算法求解该问题,同时,为了提升算法性能,专门设计了基于贪婪和随机的种群初始化方法、基于多策略的变异操作、后优化策略,并嵌入了基于破坏和修复算子的局部搜索。最后,进行了仿真实验,实验结果表明,基于聚类和距离的客户分配策略优于客户就近分配策略,改进遗传算法优于遗传算法,从而验证了基于聚类和距离的客户分配策略以及改进遗传算法的有效性。
【关键词】时变路网,多车场,车辆路径优化,碳排放,改进遗传算法
1引言
车辆路径问题是NP难问题,求解非常困难。高效的求解算法可以得到有效的车辆路径方案,有助于降低配送成本,同时提高客户满意度,因此,该问题是物流领域的研究热点[1]。与此同时,物流业是碳排放大户,随着全球对环保问题的日益重视,学者们在研究车辆路径优化时不再只考虑运输距离等经济指标,而是进一步考虑碳排放等环保指标,相应的问题则被称为绿色车辆路径问题。
近年来,绿色车辆路径问题受到了越来越多的关注。郭方明等[2]考虑客户商品需求差异和车辆异型等因素,建立了以最小化碳排放成本及总配送距离之和为目标的数学模型,并设计了一种增强型变邻域搜索算法来求解该问题。张维维[3]从低碳角度研究同时取送货的车辆路径问题,建立了以碳排放最小为优化目标的数学模型,并提出了一种结合改进的节约算法和邻域搜索算法的混合模拟退火算法来求解该问题。郭宁等[4]建立了以最小化碳排放量和最大化客户满意度为目标的数学模型,设计了一种带时间窗聚类的超启发蚁群优化算法来对该问题进行求解。葛非等[5]从最小化行驶时间和碳排放量的角度,建立了以时间成本和环境成本之和最小为目标的数学模型,并设计了一种绿色智能进化蚁群优化算法来求解该问题。
随着研究的深入,有学者在研究绿色车辆路径问题时进一步考虑了配送过程中的时变路网特性,而相应的问题被称为时变路网下绿色车辆路径优化问题。朱颢[6]同时考虑了车辆路径问题的连续时变车速、模糊需求量等特性,将绿色低碳有关的燃油成本引入目标函数,建立模糊规划模型,并利用自适应遗传算法进行了求解。郄心桐、马凯臻[7]考虑了时变速度连续变化的特点,采用多项式函数刻画车辆行驶速度,在车辆载重和客户时间窗等约束下,构建包括固定成本、碳排放成本等在内的总成本最小和客户满意度最大的多目标模型,并采用大邻域搜索操作改进NSGA-II的局部搜索能力。金渊智[8]构建了时变路网环境下考虑双目标的多车场模型和低碳车辆路径问题模型,然后设计了采用三级链表结构的带局部搜索的混合遗传算法和自约束混合遗传算法来进行求解。Soysal、Cimen[9]以最小化碳排放成本为目标进行了研究,提出了一种基于仿真的受限动态规划方法来解决该问题。Zhu、Hu[10]研究了一种考虑道路拥堵和碳排放的车辆路径问题,建立了一个以包括运输成本、碳排放成本等在内的总成本最小为目标的数学模型,并设计了一种基于粒子群优化和遗传算法的混合算法来解决该问题。
然而,上述研究主要关注单车场,目前关于多车场绿色车辆路径问题的研究还比较少,考虑时变路网特性的多车场绿色车辆路径问题研究相对更少。周鲜成等[11]采用K-Means聚类将多车场问题简化为单车场问题,构建了以成本最小化为目标的多车场绿色车辆路径模型,并使用改进蚁群算法进行求解。Fan等[12]针对时变路网下的多车场问题,考虑车辆固定成本、时间惩罚成本、燃油成本以及车速、车辆负载对油耗的影响,构建了最小化配送成本的整数规划模型,并提出了带变邻域搜索的混合遗传算法进行求解。Wang等[13]考虑速度时间依赖性和交货时间窗的分段惩罚成本,并运用运输资源共享策略,设计了一种结合节约启发式算法和多目标粒子群算法的混合启发式算法进行求解。胡蓉等[14]提出了一种绿色多车场车辆路径优化模型,并设计了一种结合蚁群算法和知识模型的学习型蚁群算法来求解这一模型。
本文研究了时变路网下考虑软时间窗的多车场绿色车辆路径优化问题,主要工作体现在以下四个方面:(1)在贴合现实配送过程的基础上,构建了该问题的数学模型,其中,同时考虑了碳排放、货损成本、车辆时变速度、车辆最大行驶距离等多种要素;(2)提出了求解上述问题的改进遗传算法,其中专门设计了基于贪婪和随机的种群初始化方法以提高种群的质量,同时设计了基于多操作的变异算子以提高算法的多样性,并嵌入了基于破坏修复算子的局部搜索以提高算法的集中性;(3)对比分析了两种不同的客户分配策略,实验结果表明,基于聚类和距离的客户分配策略优于就近分配客户分配策略;(4)将本文提出的改进遗传算法与遗传算法进行了对比,实验结果表明,改进遗传算法优于遗传算法。
2问题描述与模型构建
2.1问题描述
时变路网下考虑软时间窗的多车场绿色车辆路径问题可描述如下:现有多个车场需为多个客户实施配送,其中,每个车场拥有有限的配送车辆。同时,已知每个车场的具体位置,每个配送车辆的容量,客户的具体位置、需求量、时间窗、所需服务时间,此外,考虑到实际配送过程中存在交通拥堵,因此,在不同时间内的车辆的行驶速度不同。该问题的优化目标是求出具有最小配送总成本的路径优化方案,其中,配送总成本同时包含了经济指标成本和绿色指标成本。更具体地,该问题具有以下假设,且表1中给出了该问题的参数。
(1)所有车场的配送车辆是同质的,每辆车均从车场出发,在所有配送任务完成后返回原车场。
(2)每个客户被且仅被一个车场的一辆车服务。
(3)每个客户的需求量都小于车辆最大容量。
(4)考虑配送过程中的时变路网特性,将每天的时间分为拥挤段和非拥挤段,车辆在拥挤段和非拥挤段的行驶速度是不同的。
(5)配送车辆在行驶时产生油耗和碳排放。
(6)在配送过程中的运输和装卸环节存在货损,因此需要考虑货损成本。
(7)每个客户的服务时间窗为软时间窗,如果相应的配送车辆到达该客户的时间晚于该客户所允许的最晚服务时间,或者早于该客户所允许的最早服务时间,则产生相应的惩罚成本。
(8)车辆不得超过最大行驶距离。
(9)每个车场所拥有的车辆数是有限的。
基于聚类和距离的客户分配策略可以描述如下:首先设置聚类中心的个数为车场的数目,再利用K-Means聚类方法得到多个客户群中心,然后根据给定的多个车场坐标,计算出每个车场到客户群中心的距离,从而列出一个m×m的二维距离矩阵。矩阵中的元素表示某一个车场到客户群中心的距离,若选取矩阵中不同行不同列的m个元素,那么可以形成m!种不同的组合形式。对于每个组合,将其中的元素相加便可得到总距离,则最终可得到m!个总距离,从中选出最小的总距离,其相应的组合中车场与客户的对应关系,即为客户的分配方案。
3.2编码与解码
编码方式采用顺序编码,染色体表达形式为1~(cn+VN-1)的排列,其中cn表示该车场所服务的客户数量,VN表示该车场所拥有的车辆数。
解码过程操作可描述如下:(1)识别车场。在个体编码中找到代表车场的位置,一般为超出顾客数量的数字;(2)分割路径。根据车场的位置,将个体编码分割成多个配送路径,其中每个配送路径代表一辆车的先后配送顺序;(3)构建配送方案。将分割出的路径存储起来,所有的配送路径共同形成了配送方案。
3.3基于贪婪和随机的种群初始化方法
为了生成具有更高质量的个体,本节设计了基于贪婪和随机的种群初始化方法来生成初始种群,即分别采用贪婪算法和随机策略生成NP/2个个体,其中NP为种群规模数目。
更具体地,基于贪婪和随机的种群初始化方法的具体步骤可描述如下:
Step 1.对Step 1.1和Step 1.2重复执行NP/2次,生成NP/2个个体,即使用贪婪算法生成NP/2个个体。
Step 1.1.从cn个客户点中随机选取一个客户作为当前第一辆车首先服务的点cn1,并加入到个体中,检索未加入个体的客户点,并找到距离cn1最近的客户点cn2加入到个体中,继续在剩余未加入个体的客户点中找到距离cn2最近的客户点cn3加入到个体中,重复以上步骤,直至所有客户点均加入到个体中,由此生成长度为cn的个体。
Step 1.2.考虑车辆容量限制约束,需要根据容量约束在长度为cn的个体中依次插入(cn+1)~(cn+VN-1),将各条子路径分开,然后使每一条子路径满足载重量约束和不超过最大车辆使用数目,以确保染色体形式为1~(cn+VN-1)。否则重复Step 1。
Step 2.对Step 2.1和Step 2.2重复执行NP/2次,生成NP/2个个体,即使用随机策略生成NP/2个个体。
Step 2.1.随机生成一个包含所有客户点的全排列。
Step 2.2.考虑车辆容量限制约束和时间窗约束,需要在长度为cn的个体中插入(cn+1)~(cn+VN-1),将各子路径分开。然后将各子路径根据顾客左时间窗按照从小到大的顺序进行排序,最后使整条路径满足约束,确保染色体形式为1~(cn+VN-1),否则重复Step 2。
Step 3将Step 1和Step 2生成的NP/2个个体合并,作为初始种群。
3.4二元锦标赛选择
本文使用二元锦标赛进行选择。随机选择两个个体进行适应度比较,从中选择适应度更好的个体,重复上述步骤NP次。由于每一次比较新选出的个体可能会有重复,故删除其他重复个体,只保留重复个体中的一个。
3.5部分映射交叉操作
为了实现父代个体信息的继承,本文专门使用部分映射交叉来执行交叉操作。部分映射交叉是一种非常有效的交叉操作,已被成功地用于解决复杂的组合优化问题。部分映射交叉操作可描述如下:
Step 1.在[0,1]内生成一个随机数r,如果r<pc,转Step 2;否则,结束交叉操作。
Step 2.选择交叉点。从父代染色体中随机选择两个交叉点。
Step 3.交换基因片段。在两个交叉点之间交换父代染色体位于两个交叉点之间的基因片段。
Step 4.构建映射关系。子代染色体往往会包含重复的基因,因此需要对子代染色体进行修复。首先需要建立映射关系,在两个父代染色体中找出两个交叉点之间的基因片段,在这两个交叉片段中位于相同位置的一对基因具有映射关系。
Step 5.子代染色体修复。利用上述构建的映射关系对子代染色体进行修复,使得子代染色体没有重复和缺失的基因。
3.6基于多策略的变异操作
为了提升算法的多样性,本节设计了基于多策略的变异算子,其主要思想是使用3种策略来对解进行变异。这3种操作分别是两点交换策略、相邻元素交换策略和翻转策略,且每种操作被选择的概率均为1/3。
基于多策略的变异操作具体可以描述如下:
Step 1.在[0,1]内生成一个随机数r1,如果r1<pm,转Step 2;否则,结束变异操作。
Step 2.在[0,1]内生成一个随机数r2,如果r2≤1/3,则从染色体中随机选择两个位置,交换这两个位置上的元素;如果1/3<r2≤2/3,则从染色体中随机一个位置(最后一个位置除外),交换该位置上的元素和排在该位置之后的元素;如果2/3≤r2≤1,则在个体的基因序列中随机选择一个起始点和一个终止点,然后将这两个点之间的基因序列进行反转。
3.7基于破坏和修复算子的局部搜索
为了提高算法的集中性,本文在算法中嵌入了基于破坏和修复算子的局部搜索,其主要思想可以描述如下:对于一个解S,利用破坏算子从该解中剔除几个客户,再利用修复算子将这些被剔除的客户插入到破坏的方案中,从而得到一个新解S’,该解可能会优于原始解,如果S’优于S,则使用S’更新S。其中,破坏算子和修复算子可分别描述如下。
破坏算子:(1)随机选择一个起始顾客并加入移除集合;
(2)选择顾客并基于相关性公式计算与其他顾客的关联度;
(3)根据关联度排序和随机选择,确定下一个要移除的顾客;(4)重复步骤(2)和(3),直到达到预定的移除顾客数量;(5)从原解中移除选定顾客,形成破坏后的解。
插入算子:(1)初始化当前解为破坏后的解;(2)计算未插入顾客的最小插入成本及其位置;(3)选择最小插入成本最大的顾客进行插入;(4)将选定顾客插入到成本最小的路径和位置;(5)重复步骤(2)-(4),直到所有移除的顾客都被重新插入。
3.8重组操作
首先保留经过局部搜索操作后的全部子代个体,然后再从原始种群中选择适应度值最高的前L个个体,其中L等于NP减去局部搜索后保留的全部子代个体数目,最后将这两部分个体合并,形成新的种群。
3.9后优化策略
在达到改进遗传算法的终止条件时,本文进一步设计了一种后优化策略对改进遗传算法找到的历史最好解进行优化,该策略有助于找到更优的配送方案。
该后优化策略可描述如下:对改进遗传算法找到的历史最好解,执行基于破坏和修复算子的局部搜索,如果得到的新解优于历史最好解,则更新历史最好解,否则,不更新历史最好解。
3.10算法流程
Step 1.客户分配。使用客户就近分配策略或者基于聚类和距离的客户分配策略将每个客户分配给一个车场。针对每个车场及分配给它的多个客户,使用Step 2-12求出相应的优化配送方案。
Step 2.算法参数设置。确定改进遗传算法的算法参数NP、G、Pc、Pm,算法迭代参数g=1。
Step 3.种群初始化。使用基于贪婪和随机的种群初始化方法来初始化种群,并计算种群中每个染色体的适应度。
Step 4.二元锦标赛选择。使用二元锦标赛从种群中选择个体用于后续的部分映射交叉操作。
Step 5.部分映射交叉操作。根据交叉概率进行交叉操作,使用部分映射交叉生成子代染色体。
Step 6.基于多策略的变异操作。根据变异概率进行变异操作,从3种变异策略中随机选择一种,作为变异算子并执行。
Step 7.基于破坏和修复算子的局部搜索。对每个子代个体执行破坏和修复算子。
Step 8.重组操作。从子代种群和父代种群中选择NP个个体作为新的种群。
Step 9.终止条件判断。设置g=g+1,如果g≤G,转Step 4,否则,转Step 10。
Step 10.后优化策略。对改进遗传算法找到的历史最好解执行基于破坏和修复算子的局部搜索,如果得到的新解优于历史最好解,则更新历史最好解。
Step 11.输出历史最好解作为改进遗传算法找到的最好解。
4实验结果与分析
4.1算例描述和参数设置
为验证本文所提出的改进遗传算法的有效性,本节将改进遗传算法与遗传算法进行实验对比。所使用的算例来自https://www.bernabe.dorronsoro.es/vrp/,该算例包含4个车场和96个客户,车辆从车场出发的最早时间为7:00,回到车场的最晚时间为23:30。根据城市交通规律,将早晚高峰时间段[7:00,9:00]和[18:00,20:00]设定为拥挤时间段,而将剩余时间段设置为非拥挤时间段。在拥挤时间段和非拥挤时间段,车辆分别以拥堵速度vc和正常速度vf行驶,其中,vc和vf分别取值20km/h和40km/h。
程序采用Matlab R2021a编程实现,在CPU 2.71GHz、内存4GB的电脑上运行,模型参数取值如表2所示。将改进遗传算法的参数设置为NP=40,G=100,Pc=0.9,Pm=0.05。
4.2两种客户分配策略对比
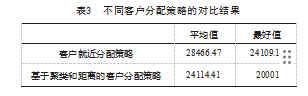
为了验证客户就近分配策略和基于聚类和距离的客户分配策略两种客户分配策略的有效性,本节通过实验对比了这两种客户分配策略,即分别使用一种客户分配策略进行客户分配,然后利用改进遗传算法独立求解10次,对比相应的配送总成本的平均值和最好值,结果如表3所示。
由表3可以看出,与客户就近分配策略相比,基于聚类和距离的客户分配策略下的配送总成本更低,平均值减少了15.29%,最好值减少了17.04%。这表明基于聚类和距离的客户分配策略优于客户就近分配策略。因此,针对时变路网下考虑软时间窗的多车场绿色车辆路径优化问题,基于聚类和距离的客户分配策略是有效的。
4.3与遗传算法对比
为了验证改进遗传算法的有效性,将其与遗传算法进行了对比,即分别使用改进遗传算法和遗传算法求解10次,对比相应的配送总成本的平均值和最好值,结果如表4所示。
由表4可以看出,与遗传算法相比,改进遗传算法的配送总成本更低,平均值减少了13.54%,最好值减少了7.72%。因此,本文提出的改进遗传算法是解决时变路网下考虑软时间窗的多车场绿色车辆路径优化问题的有效算法。
5结论
本文从数学模型和求解算法两方面深入研究了时变路网下考虑软时间窗的多车场绿色车辆路径优化问题。该研究同时考虑了多车场、时变路网、时间窗、碳排放、货损、车辆最大行驶距离等多种现实要素,因此,更加符合实际配送的特性,将为服务国家实现“双碳”目标提供技术支持。
在数学模型方面,本文通过考虑上述多种现实要素,构建了以包含碳排放成本和货损成本等在内的配送总成本最小为优化目标的数学模型,其中,还考虑了车辆不得超过最大行驶距离等约束条件。在求解算法方面,专门设计了求解该问题的改进遗传算法,同时,为了提高算法的搜索能力,专门设计了基于贪婪和随机的种群初始化方法、基于多操作的变异算子、后优化策略,并嵌入了基于破坏修复算子的局部搜索。此外,专门使用了非常高效的部分映射交叉来执行交叉操作。最后,本文执行了两类对比试验:(1)客户分配策略对比实验,实验结果表明,对于时变路网下考虑软时间窗的多车场绿色车辆路径优化问题,基于聚类和距离的客户分配策略是有效的客户分配策略;(2)算法对比实验,实验结果表明,改进遗传算法是解决时变路网下考虑软时间窗的多车场绿色车辆路径优化问题的有效方法。
[参考文献]
[1]Stamadianos T,Taxidou A,Marinaki M,Marinakis Y.Swarm intelligence and nature inspired algorithms for solving vehicle routing problems:a survey[J].Operational Research,2024,24:47.
[2]郭方明,孟祥虎,唐静,等.多商品分批次取送货的异构绿色车辆路径问题研究[J].安徽工业大学学报(自然科学版),2025,42(2):1-10.
[3]张维维.考虑碳排放的同时送取货车辆路径问题研究[D].兰州:兰州交通大学,2023.
[4]郭宁,钱斌,申秋义,等.超启发蚁群优化算法求解带柔性时间窗的绿色两级多周期车辆路径问题[J].控制与决策,2025,40(3):1-9.
[5]葛非,闵珊,邱含,等.求解时间依赖型绿色车辆路径问题的算法研究[J].计算机工程,2024,50(04):1-10.
[6]朱颢.时变环境下基于自适应遗传算法的模糊绿色车辆路径问题[J].物流技术,2023,42(10):27-33.
[7]郄心桐,马凯臻.基于客户满意度的时变绿色车辆路径问题[J].物流工程与管理,2023,45(9):25-31.
[8]金渊智.“双碳”目标背景下考虑时变路网的车辆路径问题研究[D].重庆:重庆交通大学,2023.
[9]Soysal M,Cimen M.A simulation based restricted dynamic programming approach for the green time dependent vehicle routing problem[J].Computers&Operations Research,2017,88:297-305.
[10]Zhu L,Hu D.Study on the vehicle routing problem considering congestion and emission factors[J].International Journal of Production Research,2019,57(19):6115-6129.
[11]周鲜成,吕阳,贺彩虹,等.考虑时变速度的多车场绿色车辆路径模型及优化算法[J].控制与决策,2022,37(2):473-482.
[12]Fan H,Zhang Y,Tian P,Lv Y,Fan H.Time-dependent multi-depot green vehicle routing problem with time windows considering temporal-spatial distance[J].Computers&Operations Research,2021,129:105211.
[13]Wang Y,Assogba K,Fan J,Xu M,Liu Y,Wang H.Multi-depot green vehicle routing problem with shared transportation resource:Integration of time-dependent speed and piecewise penalty cost[J].Journal of Cleaner Production,2019,232:12-29.
[14]胡蓉,陈文博,钱斌,等.基于学习型蚁群算法的绿色多车场车辆路径问题研究[J].系统仿真学报,2021,33(9):2095-2108.
[15]解玉蝶.考虑时间窗和碳排放的冷链物流路径优化研究[D].无锡:江南大学,2022.
[16]董冬艳.基于生鲜农产品的冷链物流配送路径优化研究[D].沈阳:沈阳大学,2018.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/82460.html