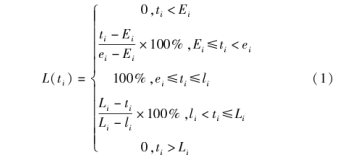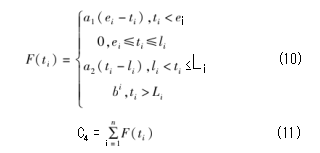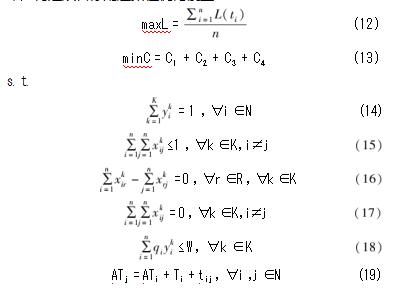【摘要】为优化物流配送路径,提高客户满意度,通过综合考量顾客对货物配送时效的需求、企业对配送成本的管控和环境对碳排放量的制约,建立以最大客户满意度和最小物流配送成本为目标的双目标车辆路径优化模型。以华东某物流公司为例,选择NSGA-Ⅱ算法对模型问题进行求解,并将得到的Pareto解根据层次分析法选出最优的解,以检验建模和算法的可行性和合理性。
【关键词】双目标模型,客户满意度,碳排放
随着经济的飞速发展,物流企业的市场竞争不断加剧,导致企业的品牌形象在市场中也变得越来越重要,而客户满意度是企业品牌形象建设中不可或缺的一部分,因此,对车辆配送路径问题的研究需要考虑客户满意度这一因素[1]。在物流运输规划过程中,首先要考虑的就是控制运输成本。同时,随着全球低碳经济的发展,低碳也成为了车辆路径问题中所需考虑的目标之一。因此,如何降低成本、提高客户满意度、减少碳排放量是车辆运输路径规划中急需解决的问题。
随着对车辆路径配送问题的研究逐渐深入,学者们基于现实的配送过程,提出了带有时间窗的车辆路径配送问题,此类问题所考虑的是配送车辆过早或者过晚送达从而影响客户的满意度[2]。Jabali等[3]引入了软时间窗,构建了车辆路径优化模型并设计遗传算法对其进行求解。赖平仲等[4]在考虑客户的期望时间窗的基础上,在交通限行的条件下构建了以最低配送成本为目标的车辆路径优化模型。Song,Ko[5]对易腐产品的运输路径问题进行研究,以客户最优满意度为目标建立了模型并进行求解。邓红星等[6]引入软时间窗,构建了以最小成本为目标的车辆路径优化模型,并且利用改进的遗传算法对其进行求解。
随着“碳达峰、碳中和”的提出,已经有不少国内外学者在对车辆路径问题进行研究时考虑低碳因素。吴丽荣等[7]为了减少车辆碳排放,构建了车辆燃料消耗的模型并对其进行求解。康凯等[8]构建车辆路径优化模型,引入模糊约定时间窗,并考虑碳排放因素,使用遗传算法对其进行求解。代楚楚,徐菱[9]构建了基于时间依赖的车辆路径选择模型,引入碳排放机制,并且设计遗传算法对其进行求解。李文霞等[10]以最小化成本、周转时间及碳排放为目标构建模型并对其进行求解。珠兰等[11]在环境污染的背景下,考虑交通拥堵对配送路径的影响,研究基于时间依赖性的车辆路径优化问题。
目前,许多专家学者已经对车辆路径问题进行了研究,并且取得了一定成果。但实际上,同时考虑物流运输所涉及的企业、客户和社会环境的研究较少[12]。并且在目前多目标车辆路径优化模型的求解过程当中,绝大多数学者依旧选择如主要目标法和约束法等传统方法对其进行求解,也未能将各目标进行合理的量化。
因此,本文综合考虑运输相关利益主体,对考虑客户满意度的双目标车辆路径优化问题进行研究,将到达时间作为衡量客户满意度的标准,考虑低碳因素,构建以最大客户满意度与最小成本为目标的数学模型,并且在提出双目标模型的基础上采用NSGA-Ⅱ算法求出帕累托解,再利用层次分析法量化各目标的重要程度,得到两个目标的权重,最后求出最优解。
1问题描述及条件假设
1.1问题描述
考虑客户满意度的双目标车辆路径优化问题可以被描述为:在城市网络中存在一个配送中心和若干个客户需求点;配送中心根据每个客户点的需求量以及期望服务时间窗进行分配运输;车辆从配送中心0出发,按照路线进行配送,最终返回到配送中心。
1.2条件假设
鉴于实际问题的复杂性和不确定性,模型建立基于如下假设:
①配送车辆的车型以及最大运载量相同;
②在配送过程中车辆始终保持匀速行驶;
③各个需求点仅有一辆车为其进行配送,同时需求量提前获知且不可拆分;
④配送中心及需求点之间的行驶距离已知且车辆的始末点均为配送中心;
⑤配送路程不考虑交通堵塞、天气影响等特殊情况。
2模型构建
2.1参数定义
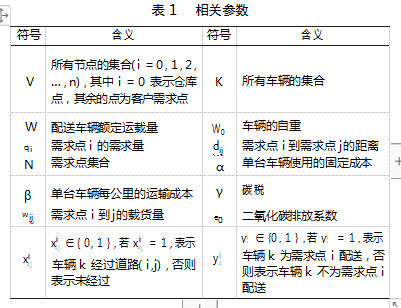
本文模型中定义的相关参数如表1所示。
2.2模型目标函数构建
2.2.1客户满意度目标
本文以到达时间来衡量客户满意度。客户满意度函数L(ti)与车辆到达时间ti的关系如图1所示。
其中,当配送车辆到达客户点的时间在客户接受时间之内,但在其所期望的服务时间之外的[Ei,e i]和[li,Li]区间内送达时,客户满意度与到达客户点的时间呈线性相关;当配送车辆到达客户点的时间在客户所期望的服务时间[ei,li]区间内时,客户满意度为最大值1。当配送车辆到达客户点的时间在客户能够接受服务的时间[Ei,Li]之外时,客户满意度为0[13]。客户满意度函数如下:
本文将客户满意度表示为客户点的平均满意度,具体公式如下:
2.2.2成本目标
车辆配送的总成本由固定成本、运输成本、碳排放成本和惩罚成本构成。
①固定成本。
固定成本是指车辆进行配送时产生的初始成本,包括车辆的购买成本、人工成本和维修成本等。本文中每辆车的固定成本已知,总固定成本与配送车辆数成正比,用C1表示配送的总固定成本,具体公式如下:
②运输成本。
运输成本是指配送过程中所有配送车辆产生的费用之和,与车辆行驶路径长度成正比。本文用C2表示运输成本,具体公式如下:
③碳排放成本。
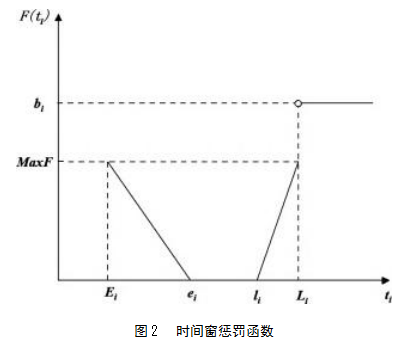
惩罚成本是指车辆没有在规定时间窗内将货物送至客户点而产生的机会损失和延误惩罚。时间窗惩罚函数如图2所示。
由图2可知,时间窗的惩罚函数被划分为三部分,第一部分为配送车辆到达客户点的时间ti早于客户期望时间e i,将造成机会损失并产生费用;第二部分为配送车辆到达客户点的时间在期望时间li与最晚接收时间Li范围内,此时造成延误并产生惩罚费用,惩罚成本与延误时间呈线性关系,且达到的最大惩罚成本为MaxF;第三部分为配送车辆到达客户点的时间晚于最晚接收时间点Li,产生的惩罚成本将达到最大值b i[15]。F(ti)为时间窗惩罚函数,总惩罚成本用C4表示,具体公式如下:
2.3建立双目标车辆路径优化模型
本文在设计配送方案时,同时对客户满意度和配送成本进行优化处理,在保证客户满意的情况下尽可能降低配送成本,构建双目标配送路径优化模型:
其中,式(12)表示最大化客户满意度;式(13)表示最小化配送成本,由固定成本、运输成本、碳排放成本和惩罚成本共同构成;式(14)表示每个需求点只有一辆车为其进行配送;式(15)表示每一辆车只进行一次配送;式(16)表示车辆运输路线的连续性;式(17)表示相同客户需求点之间没有服务路线;式(18)表示车辆载货量约束;式(19)表示某条路径中两节点间车辆抵达时间的联系。
3 NSGA-Ⅱ算法设计
在前文建立的双目标车辆路径优化模型中,两个目标之间存在此消彼长的现象,无法均取到最优值,通常只能求得相对意义上的帕累托最优解[16]。有两种解决此类多目标问题的方法,一种为传统方法,例如线性加权法、主要目标法等,这类算法将多目标模型转化为单目标模型后进行求解,带有较大的主观性。另一种为智能算法,此类算法可以在不主观赋权的情况下求得多个帕累托最优解,有效地克服了传统求解算法的局限性。
NSGA-Ⅱ算法针对NSGA算法进行了如下改进:①采用快速非支配排序算法,大大降低了算法的复杂度[17];②采用拥挤度和拥挤度比较算子,提高了种群的多样性;③采用了精英策略,提高了算法的运算速度和鲁棒性,保留了优秀个体[18]。因此,本文针对双目标路径优化模型设计NSGA-Ⅱ算法对其进行求解。
3.1染色体编码和解码
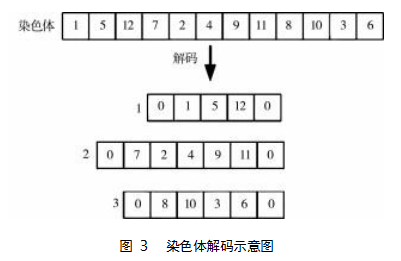
本文选择自然数编码方式。0表示配送中心,1,2,3,…,n表示客户需求点,K表示最大车辆数。染色体长度为n+K-1,染色体为(1,2,3,…,n,n+1,…,n+K-1)的随机排列,配送分割点为(n+1,n+2,…,n+K-1)。图3以12个客户和3辆车的配送方案为例,染色体为(1,5,12,7,2,4,9,11,8,10,3,6),11和12表示分割点,通过解码得到配送路线的方案。可知车辆1从配送中心出发,依次为客户点1、5、12进行配送,然后返回配送中心0;车辆2从配送中心出发,依次为客户点7、2、4、9、11进行配送,然后返回配送中心0;车辆3从配送中心出发,依次为客户点8、10、3、6进行配送,然后返回配送中心0。
3.2快速非支配排序和拥挤度比较
NSGA-Ⅱ采用快速非支配排序。快速非支配排序就是将解集分为不同等级的帕累托前沿的过程,即确定种群中两两个体的支配关系,根据解集中每个解所支配的解的集合及其被支配的数量来确定解的帕累托等级。
拥挤度比较是为了衡量同一个帕累托前沿中解质量的优劣。当两个解都属于同一个帕累托前沿时,对比两个解在当前等级解集中周边解的密集程度,优先选择拥挤距离大的解,有效提高种群多样性。
3.3初始化种群
算法的迭代需要在一个初始种群上进行,算法的收敛性对初始解的质量依赖性较强。因此本文使用完全随机生成法,根据车辆最大运载量的约束条件初始化染色体。考虑车辆运载量约束,若∑=1qj≤W且∑qj>W时,在第r个客户和r+1个客户之间插入0。
3.4选择、交叉与变异
本文采用二元锦标赛作为选择算子。具体步骤如下:选择父代种群中最优的个体作为子代,不断循环重复,直至得到下一代循环的初始种群[19]。其优势在于降低计算的复杂度,有利于保留种群中优质个体。
本文采用部分匹配交叉的交叉方式。具体步骤如下:将父代个体中两个交叉位置之间的片段进行交叉,然后对片段外重复的部分进行调整。交叉算子主要是为了获得适应度更高的个体。
本文采用逆转变异的变异方式。具体步骤如下:将在父代中随机选取的基因串进行逆转,再放入子代相对应的位置,最后将父代其余位置的基因依次放入子代相对应位置。如染色体为(1,5,12,7,2,4,9,11,8,10,3,6),变异后生成(1,5,12,7,11,9,4,2,8,10,3,6)。变异算子主要是为了保护个体的多样性。
3.5精英策略
NSGA-Ⅱ算法引入精英策略,可增大搜索空间。精英策略是指将每次循环得到的父子种群中的优秀个体保留到下一次迭代的初始种群中,有助于有效保留种群中优秀的个体,淘汰劣等个体,提高计算的效果[20]。图4为精英策略执行步骤。
4算例验证
4.1算例说明
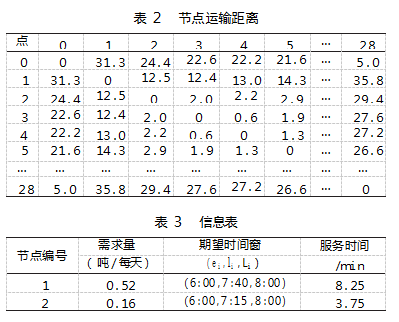
为验证双目标车辆路径优化模型与NSGA-Ⅱ算法的合理性与有效性,以华东某物流公司作为参考进行模拟。以某一次配送服务为例,一共有28个客户需求点,配送中心0为其提供配送服务。各节点间运输距离如表2所示。需求量、期望时间窗、作业时间等信息如表3所示。
4.2算法对比
NSGA-Ⅱ算法中的参数设置如下:种群规模为100,最大迭代次数为300,交叉概率为0.7,变异概率为0.1。
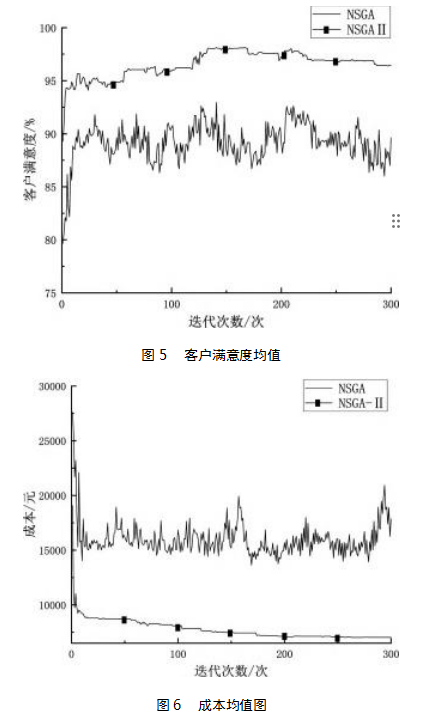
为体现出NSGA-Ⅱ算法的优势,将NSGA与NSGA-Ⅱ两种算法进行对比。各代单目标函数的平均值变化如图5和6所示。
从图中可以看出,NSGA-Ⅱ算法明显优于NSGA算法,所求单目标平均值较NSGA更优,所以利用NSGA-Ⅱ算法有一定的有效性与合理性。
4.3结果分析
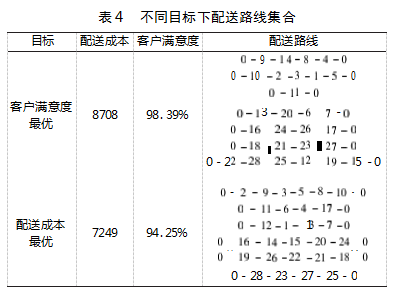
NSGA-Ⅱ算法最终求得帕累托最优解集,表4为不同目标下车辆路线集合。
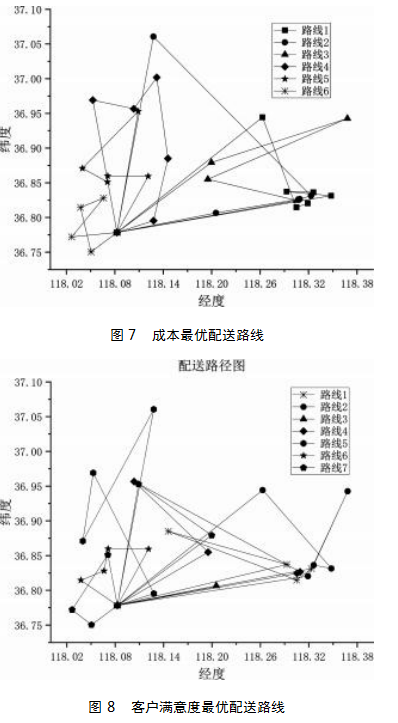
使用NSGA-Ⅱ算法进行求解时,无法求得双目标均为最优的解,而是得到了一系列帕累托解。当决策者偏向于配送成本最优时,配送路线如图7所示,决策者所选路线的客户满意度较其最优减少了4.14%;当决策者偏向于客户满意度最优时,配送路线如图8所示,决策者所选路线的配送成本较其最优增加了1459元。对于企业来说,为了降低成本就需要牺牲一定的客户满意度。
4.4综合评价
4.4.1数据处理
将运行的帕累托解集进行无量纲化处理。
对于正向指标即客户满意度指标进行如下处理
4.4.2 AHP决策
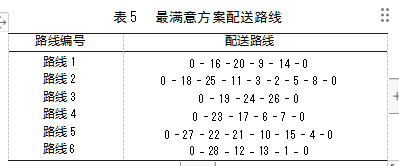
通过5位专家打分对客户满意度和运输成本的重要程度进行量化处理。决策时成本是最重要的目标,其次是客户满意度。最终得到的平均权重向量为M=(0.218 0.782)T,评价方案的矩阵为G=AMT。最终选择最满意方案为maxG=0.698时,L=0.9487,C=7467,其配送路径如表5所示。
5结论与展望
本文以考虑客户满意度与碳排放的车辆路径优化问题为研究方向。为提高客户满意度、降低成本,研究引入期望时间窗函数与时间窗惩罚函数,同时为了考虑绿色低碳运输,在成本中加入碳排放成本,建立以最大客户满意度和最小成本为目标的双目标车辆路径优化模型,并针对模型设计NSGA-Ⅱ算法来进行求解,然后将计算得到的帕累托解集进行处理,并根据AHP决策选出最优解。结果表明,本文设计的多目标路径优化模型和NSGA-Ⅱ算法具有一定的有效性和合理性,AHP决策能为决策者求得满意的运输路径,为车辆路径优化问题提供了一定的参考意见。然而,本文仍有许多不足之处,如在建立模型时并未考虑到模型的复杂程度,没有考虑配送道路拥堵、天气等多种因素对于路径选择的影响,可以在未来进一步做深入研究。
[参考文献]
[1]郄心桐,马凯臻.基于客户满意度的时变绿色车辆路径问题[J].物流工程与管理,2023,45(09):25-31.
[2]吕垚远,张春美.考虑顾客满意度的多目标车辆路径优化问题 [ J] . 太原科技大学学报,2023 ,44(06) :527 - 534.
[3]Jabali O,Leus R,Van Woensel T,et al.Self-imposed time windows in vehicle routing problems[J].OR Spectrum,2015,37(2):331-352.
[4]赖平仲,汤洋,杨珍花,等.考虑城市货运车辆交通管制的配送优化[J].大连海事大学学报,2015,41(4):59-66.
[5]Song B D,Ko Y D.A vehicle routing problem of both refrigerated-and general-type vehicles for perishable food products delivery[J].Journal of Food Engineering,2016,169:61-71.
[6]邓红星,刘敏,王猛.基于随机需求的冷链物流路径优化问题研究[J].交通科技与经济,2020,22(1):1-6.
[7]吴丽荣,胡祥培,饶卫振.考虑燃料消耗率的车辆路径问题模型与求解[J].系统工程学报,2013,28(6):804-811.
[8]康凯,韩杰,马艳芳.基于碳排放的模糊约定时间车辆路径问题研究[J].工业工程与管理,2017,22(4):17-22.
[9]代楚楚,徐菱.考虑碳排放的快递企业配送路径研究[J].铁道运输与经济,2015,36(7):70-77.
[10]李文霞,张春民,马昌喜.多目标低碳车辆路径优化模型及求解算法[J].交通信息与安全,2020,38(1):118-126+144.
[11]珠兰,马潇,刘卓凡.时间依赖型绿色车辆路径问题研究[J].交通运输系统工程与信息,2021,21(6):187-194.
[12]田爱玄.交通限行背景下多目标城市配送路径优化研究[J].中国储运,2022,262(07):136-138.
[13]蓝远.模糊时间窗约束下的冷链物流车辆路径问题研究[D].广州:华南理工大学,2018.
[14]董洁美.考虑碳排放和多配送中心的便利店配送路径优化研究[D].南京:南京大学,2021.
[15]孙艺婕.带时间窗的城市物流多中心配送路径优化研究[D].舟山:浙江海洋大学,2020.
[16]常海平,李婉莹,董福贵,等.基于NSGA-Ⅱ的冷链物流配送路径多目标优化[J].交通科技与经济,2022,24
[17]燕嘉诚,印凯欧.基于NSGA-Ⅱ的信息物理系统RESTful API测试套件最小化[J].计算机与现代化,2022(11) : 111 - 118.
[18]张珂.基于NSGA-Ⅱ算法的大规模路网危险品运输路径选择[J].物流工程与管理,2022,44(10):151-153.
[19]朱兴林,罗丽朝,温喜梅,等.不确定条件下公路应急资源点选址鲁棒优化[J].交通科技与经济,2022,24(03):41-49.
[20]罗苇杭.基于非支配排序遗传算法的时变时间窗多目标车辆路径问题研究[D].济南:山东大学,2020.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/78006.html