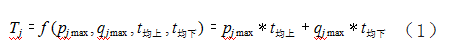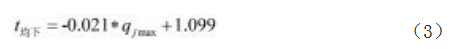SCI论文(www.lunwensci.com):
摘 要:乘客乘降时间是城市轨道交通列车停站时间的重 要组成部分, 列车停站时间关系轨道交通系统的运行效率和服务水平。本文将乘降时间划分为上车和下车两个独立 的阶段,对乘客乘降行为及影响因素进行了调查与分析,建立了乘客乘降时间估计模型,并根据实测数据,拟合了乘客 平均上下车时间与乘降人数和列车满载率之间的函数关系。 以上海地铁9号线为例进行了分析,结果表明该估计模型计 算结果精度较高。该研究成果可以为城市轨道交通线路计划 停站时间方案的制订与优化提供一定的方法参考。
关键词:城市轨道交通;乘降时间;影响因素;优化方法
随着城市轨道交通快速发展,越来越多的人选择 乘坐地铁出行。在地铁车站中,乘客上下车是主要的 交通活动之一[1] 。乘客乘降时间是确定地铁最小停站时 间的一个关键因素,列车乘降时间预留过长,超过乘 客乘降需求时间,导致停站时间浪费;乘客乘降时间 预留过短,可能仍有乘客未完全上下车,导致屏蔽门 车门夹人等安全事故发生。因此,合理确定乘客乘降 时间是城市轨道交通运行图编制的重要内容,对地铁 运行效率具有较大影响。
综合国内外相关研究发现[2 ,4] ,对城市轨道交通 乘客乘降时间的研究通常采取实测数据分析与仿真两 种方法。本文基于上海轨道交通乘客乘降时间观测数 据,分析了乘客乘降时间影响因素,建立了乘客乘降 时间估计模型,并进行了实例研究。
一、乘客乘降时间影响因素分析
列车停稳后,乘客有序上下车,乘客乘降时间可 分为上车时间及下车时间两个阶段进行研究[5] 。本文基 于上海地铁世纪大道、南京东路、浦电路等6个车站的 站台监控视频进行数据采集,并对乘客乘降行为与乘 降时间数据进行分析。
(一)乘客乘降人数越多,乘降时间越长
乘客乘降时间随乘客人数的增加而增加,但乘客 人数与乘降时间之间并不是简单的线性关系。当乘客人数较少或列车车厢内较为拥挤时,乘客上车速度会变 慢;当乘客人数较多或列车车厢内还有剩余座位数时, 由于乘客急于抢占座位等原因而会加快上车速度。
(二)乘客平均上车时间随上车人数增加而减 少,随着车内拥挤度增加而增加
本文根据现场观测数据和运营企业提供的列车实 时满载率数据[6] ,绘制乘客平均上车时间与列车满载 率、上车人数之间的三维散点图,如图1所示。列车车 厢越拥挤,乘客越难进入列车,甚至无法上车。为进 一步探究其关系,分别进行双变量分析。结果表明, 平均上车时间与上车人数皮尔逊相关系数为-0.708, 平均上车时间与列车满载率皮尔逊相关系数为0.449, 显著性相关系数均小于0.001。由分析可知, 乘客平均 上车时间与上车人数、列车满载率具有显著相关性。
(三)乘客平均下车时间随下车人数的增加而减少
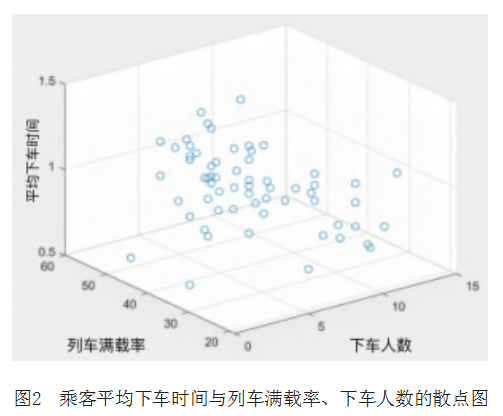
列车到站前,需要下车的乘客往往提前在车门前 候车,候车人数越多,下车时间越久。同理,本文绘 制乘客平均下车时间与列车满载率、下车人数的三维 散点图,如图2(详见第47页)所示。进一步进行双 变量分析,结果表明乘客平均下车时间与下车人数之 间的皮尔逊相关系数为0.812,显著性相关系数小于 0.05;乘客平均下车时间与列车满载率之间的相关系 数为-0.378。可知,乘客平均下车时间与列车满载率无关。
二、乘客乘降时间估计方法
(一)模型基本假设
乘客乘降时间取决于最大客流车门处乘客上下车 所需时间,计算时需考虑站台上乘客分布情况以及乘 客上下车过程对乘降时间的影响。为简化计算,本文 对模型做出以下假设:
(1)乘客严格按照先下车后上车的秩序进行, 上、下车客流不互相干扰;
(2)对于岛式站台,忽略对向客流间的相互干扰;
(3)假设乘客无滞留情况,候车乘客在列车到达 后即能全部上车。
(二)乘客乘降时间估计模型
每列车所需的乘客乘降时间估计值应保证最大排队 候车车门前的乘客完成乘降过程。因此,分上车和下车 两个阶段,考虑车门最大乘降人数以及乘客平均乘降时 间,建立乘客乘降时间估计模型,如式(1)所示。
式(1)中, Tj 是指车站j某运行方向某时段列车的 乘客乘降时间估计值,s; pj max 和qj max 是指车站j某运行 方向某时段该列车乘降人数最多的车门前的上车或下 车人数,可以根据轨道交通分时段全网OD斜表、列车 发车间隔等数据进行计算[3] ;t均上 和t均下 是指乘客平均 上车或下车时间,s/人。
进一步,根据现场观测数据和前述影响因素相关性 分析,拟合得到乘客平均上车时间与上车人数和列车满 载率ε之间的回归方程,见式(2);拟合得到乘客平 均下车时间与下车人数之间的回归方程,见式(3)。
经检验,平均上下车时间回归标准化残差基本符 合正态分布,满足线性回归模型要求,如图3所示。模 型调整后判定系数R2为0.851,具有较好的拟合优度。
三、案例分析
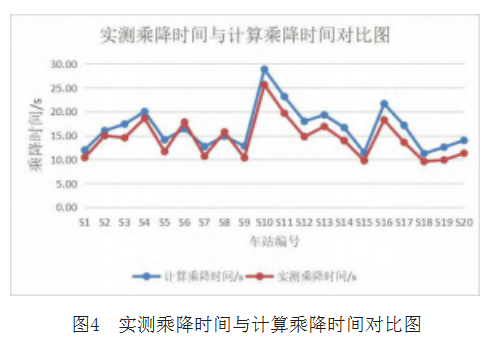
为检验上述乘客乘降时间估计模型的精确度,本 文基于车站监控视频数据采集了工作日早高峰上海轨 道交通9号线洞泾站至世纪大道站共20个车站(编号为 S1~S20)的车门前上下车人数和乘降时间。基于上述 估计方法计算各站的乘降时间,对比实测乘降时间及 计算乘降时间,如表1和图4(详见第48页) 所示。
由表1和图4分析可知,计算乘降时间与实测乘 降时间误差最大为3.48s,最小为0.90s,平均误差为 2.11s,说明该模型具有较高的精度。比较发现,当总 乘降人数超过15人时,乘客乘降时间误差相对较大,其主要原因是各站各列车的实际乘降时间具有一定波 动性。该实例是基于某一时段的统计客流数据值得到 计算乘客乘降时间,因此某一列次的乘客实际乘降时 间与计算乘降时间可能存在一定范围的误差。
四、结语
合理确定乘客乘降时间关系到轨道交通系统的运 行效率和服务水平。本文基于实测数据,对乘客乘降 行为及影响因素进行了分析,建立了乘降时间估计模 型,并拟合了乘客平均上下车时间与乘降人数和列车 满载率之间的函数关系。以上海轨道交通9号线为例,进行了实证研究,实例分析表明,本文提出的估计模 型精度较高,期望可以为城市轨道交通线路计划停站 时间方案的制订与优化提供一定的方法参考。
参考文献
[1] 韩宇,韩宝明,李得伟.地铁站乘客上下车效率因素影响 分析[J].城市轨道交通研究,2007(7):43-46.
[2] 王亚飞.城轨交通站台乘客上下车运动和实验研究[D].北 京:北京交通大学,2016.
[3] Jiang Z ,Xie C ,Ji T ,et al.Dwell time modelling and optimized simulations for crowded rail transit lines based on train capacity[J].PROMET-Traffic&Transportation,2015, 27(2):125-135.
[4] 曹守华,袁振洲,赵丹.城市轨道交通乘客上车时间特性 分析及建模[J].铁道学报,2009,31(3):89-93.
[5] 陈伽申,蒲琪,涂颖菲.城市轨道交通乘客上下车行为与 停站时间研究[J].城市轨道交通研究,2017,20(1):61-64,78.
[6] 王思韬,蒲琪.二次关门对城市轨道交通列车停站时间的影响[J].城市轨道交通研究,2019,22(7):53-57.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/guanlilunwen/71798.html