SCI论文(www.lunwensci.com):
摘 要:传统的工厂模式的教育体系下,由于时间、空间、技术等多个因素的限制,学习者很难在传统的课堂上达成深度学习的目标。如今,互联网、大数据、人工智能的飞速发展,突破了之前的种种限制,MOOC、翻转课堂、 移动学习等方式给学习者带来了新的体验,但学习的碎片化、微型化、在线化也带来了一系列新的问题,学生的学习只停留在浅层学习,并不能达到深度学习。本文提出了在信息化背景下应用精密教学策略来促进深度学习的具体思路,以期让批量化、可复制的深度学习成为可能。
关键词:深度学习;教学策略;认知等级;精密教学;学习行为
本文引用格式:李珩,彭静 . 信息化环境下促进深度学习的精密教学策略研究 [J]. 教育现代化 ,2021,8(39):130- 133,144.
research on Precision Teaching Strategy to Promote deep Learning in Information Environment
LI Heng1,PENG Jing2(1. Center for Enhancement Teaching and Learning, Chong Qing University, Chongqing; 2. School of Foreign Languages Cultures, Chong Qing University, Chongqing)
Abstract: Under the traditional factory mode education system, due to the limitations of time, space, technology and other factors, it is difficult for learners to achieve the goal of deep learning in the traditional classroom. Now, due to the Internet, big data and the rapid development of artificial intelligence, modern education has breached the restrictions. Though MOOC,flip classroom and mobile learning brought new experiences to the learners, learning fragmentation, miniaturization and online learning also bring a series of new problems, students learn to stay on the shallow, and can’t reach deep learning. This paper proposes a specific idea of applying precise teaching strategies to promote deep learning under the information background, in order to make mass and reproducible deep learning possible.
Keywords: deep learning; teaching strategies; cognitive level; precision teaching; learning behavior
一 深度学习的提出
1900 年,美国的教育者参照了工业体系中出现的有效工厂体系,创造了一个通用的教育体系:学生按年龄划分年级,按年级将学生安排在不同的教室并配备一名教师,教学和测试都被标准化。在那个年代,这种工厂模式的教育培养了大量的学生, 但这些学生所从事的工作大部分不需要更高层次的教育,只有大概 17% 的工作需要知识型人才。随着科学技术飞速发展,超过 60% 的工作都需要知识型人才,按照布鲁姆的学习目标分类,现代的人才培养更加重视高阶目标的达成。学术性的知识和技能本身不能使学生成为适应和驾驭未来的人,学生还必须知道如何分析、评判、协作、创造和创新。
要实现这一人才培养的目标,教学模式和学习方式都面临着重大的变革,而这其中引起教育者们最为广泛关注的热点之一便是深度学习。1976 年, 在《学习的本质区别一 : 结果和过程》一文中,瑞典的费伦斯·马顿和罗杰·萨尔乔 首次提出了深度学习 ( Deep Learning) 和浅层学习 ( Surface Learning) 这两个概念 [1]。2005 年, 黎加厚等人从布鲁姆的教学目标分类学的角度对深度学习进行了界定,他认为浅层学习的认知水平停留在前两层,而深度学习的认知水平对应着后四层 [1]。
郭华认为深度学习就是在教师引领下,学生以具有挑战性的学习主题,全身心积极参与、体验成功、获
得有意义的学习过程 [2]。何克抗提出:深度学习以全新的理念、方式和必要的工具、资源和手段来达到高级深层认知能力尤其是创造能力,不仅能记忆、理解各学科基础知识,还可对基础知识做分析与评价,并创造新知识和新产品 [3]。
学习者如何才能摆脱浅表层的学习,实现高阶思维的深度学习呢?在过去,教育者们往往依赖于一些比较传统教学策略,如基于问题的学习、任务驱动式的学习、基于过程性的评价 [1] 等等来促进学习者的深度学习。然而,在传统的工厂模式的教育体系下,由于时间、空间、技术等多个因素的限制, 学习者很难在传统的课堂上达成深度学习的目标 [4]。如今,互联网、大数据、人工智能的飞速发展,突破了之前的种种限制,MOOC、翻转课堂、移动学习等方式给学习者带来了新的体验,但学习的碎片化、微型化、在线化也带来了一系列新的问题,学生的学习只停留在浅层学习,并不能达到深度学习 [4]。深度学习需要通过运用多步骤的分析与加工策略,如概念转变、认知结构养成、资源交互、反思再认等, 以期获得对知识的深层认识 [5]。因此,不仅仅要借助于信息化的力量,同时要结合有效的教学策略,方能使得深度学习达到理想的效果。
本文提出了在信息化背景下应用精密教学策略来促进深度学习的具体思路,以期让批量化、可复制的深度学习成为可能。
二 认知发展理论
瑞士心理学家皮亚杰在其发生认识论、运算逻辑和儿童心理学体系中提出了关于儿童认知发展可以分为四个阶段的理论,这四个相继而又有质的差异的阶段是:
(1)感知运动阶段;(2)前运算阶段;(3)具体运算阶段;(4) 形式运算阶段。皮亚杰认为,在个体从出生到成熟的发展过程中,认知结构在与环境的相互作用中不断重构,从而表现出具有不同质的不同阶段,尽管不是所有儿童都在同一年龄完成相同的阶段,但通过各个阶段的顺序是一致的,前一阶段是达到后一阶段的前提 [6]。阶段的发展不是间断性的跳跃,而是逐渐、持续的变化。
皮亚杰以逻辑与运算的数理工具对儿童内部心理结构进行的系统性分析 , 对当代心理学与教育学的发展产生了巨大影响,从中我们得到的启发是:人类认知的生长取决于个体自身思维运演活动,遵循着独特的发展步调与结构规则。但皮亚杰理论的局限性在于:仅仅包括了儿童及青少年阶段;理论局限于解释逻辑、数学及科学学科方面的问题。在皮亚杰理论的基础之上,结合 Dawes 等提出的标准数学模型 (Coombs, Dawes, and tversky, 1970)[7] 和信息科学(Commons and Richards, 1984a, 1984b;Commons and Rodriguez, 1990, 1993; 林赛和诺曼,1977)[8], 哈佛大学的 Commons 教授提出了等级复杂度模型 MHC(Model of Hierarchical Complexity), 该模型由一个 16 层的等级来描述不同的认知阶段(见表 1)。
其中前四个等级 0-3 对应了皮亚杰的感知运动阶段, MHC 的 4-6 阶段对应了皮亚杰的前运算阶段,6-8 对应了具体运算阶段,9-11 对应了形式运算阶段, 12-15 最后四个高级阶段没有出现在皮亚杰的模型中。0-5 通常发生在人的婴儿期和幼儿期。MHC 的主要思想在于:学习者理解发展的阶段是由层级顺序构成的,每一个阶段(层级)都是为下一个阶段(层级)所需的基础。比如语言学习,我们基本上都是按照发音 - 单词 - 句子 - 段落的顺序进行学习,每一个新动作 / 理解都依赖于成功完成前的一个步骤。
MHC 在皮亚杰的基础上对认知的等级进行了进一步的细化,对于深度学习而言,不同的认知等级让深度学习有了可测量的依据, 深度学习者将追求更高的认知等级的达成。目前的教学策略不能很好地了解学生的认知发展阶段,不同认知阶段的学生用不同的方式处理知识,而老师用同样的教学方法对待认知阶段不同的学生, 并主要依赖于考试以及分数来衡量学生对知识的掌握程度。
三 促进深度学习的精密教学策略
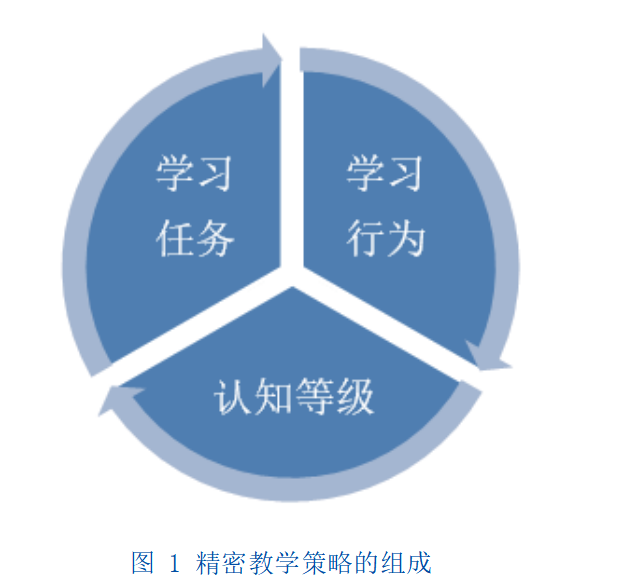
(一) 精密教学策略的基本模型
精密教学策略是根据学习者对知识流畅程度的测量,来最大限度的达到深度学习的效果。精密教学策略由三个部分构成,如图 1 所示:认知等级、学习行为和学习任务。
认知等级是基于 MHC 所规定的理想形式,用于复杂性级别的构造。认知等级的先后顺序是客观的,并且在本质上是定量的:与之相匹配的学习任务要么是能正确完成的,要么不能完成,没有中间状态。具体来说,比如完成两个数字加法的任务 : 学习者只能正确地做或根本不能做。
学习任务的复杂程度各不相同,任务的表现由认知等级的不同阶段来衡量。每个学习任务的难度都有一个层次复杂度的顺序,以便学习者能正确地完成它,如果想要达到下一个认知等级,需要完成以下任务:该任务是由至少两个不一样的难度较低的任务组成;能够整合这些难度层次较低的任务。例如,掌握数字和加减法的任务是执行乘法任务的必要条件。成功完成加法和乘法任务是两个不同阶段的任务的例子,可以使用认知等级来量化。这一目标、任务和阶段的量子特征意味着可以给它们分配离散的分数。
学习任务的复杂性有两种不同的类型:水平的和垂直的。水 平 复 杂 度 源 自 经 典 信 息 论 (Shannon and Weaver, 1949)[9],指的是完成一项任务所需要的“是 -否”问题的数量。例如,当一个人问另一个人关于翻转硬币后是否正面朝上的问题时,这实质上是传递了 1 比特的“ 水平” 的信息, 当有两个硬币时, 就需要至少针对每个硬币问一次。因此,每增加一个额外的信息就会增加一个比特。水平复杂度是由所有关于事件的比特信息累计而成。再举例来说, 如果有一个四面体的四个面的编号为 1,2,3,4, 当有人想知道在它抛起来降落后是哪个数字出现在最上面,可以先问最上面的数字是不是偶数,如果是, 可以继续追问是不是 2 以需求最后的答案,因此本次信息的积累只需要 2 个比特,就能在没有亲眼看到的情况下推断出顶部的数字。
垂直复杂度也可以看作层次复杂度,较高层次的任务由较低层次的子任务构成。另一种说法是, 较为简单的任务是由更复杂的任务组织协调的。垂直复杂度由执行一组相关联的任务的递归的次数构成,递归涉及到每个层次任务的复杂度。
学习行为可以看作对学习任务的反馈。学习行为和认知等级一样,本质上也是定量的。也就是说, 没有中间行为。由于层次复杂性模型提出了将旧操作组合成新操作的阶段变化一致性,因此讨论可能发生的各种低阶操作组合的数量非常重要。有迭代、混合、链和新阶段的行为。迭代就是一遍又一遍地做同样的动作。例如,添加 1 + 2 + 3 + 1 + 2 + 3 是一个添加的迭代。混合操作可能包括做一个包含简单加法和简单乘法任务的问题集。链包含子任务操作的顺序,但是顺序是任意的。例如,有人可以在早上醒来, 开始煮咖啡,然后进行锻炼。顺序是任意的,因为顺序可以颠倒,例如,锻炼计划可以在开始煮咖啡之前完成。根据该模型,当任务以非任意顺序组合,然后进行协调。因此,当两个或多个较低阶段的任务得到协调时,就出现了新阶段的行为。
( 二 ) 精密教学策略的步骤
1.设定认知等级,并为相应等级匹配对应的学习行为
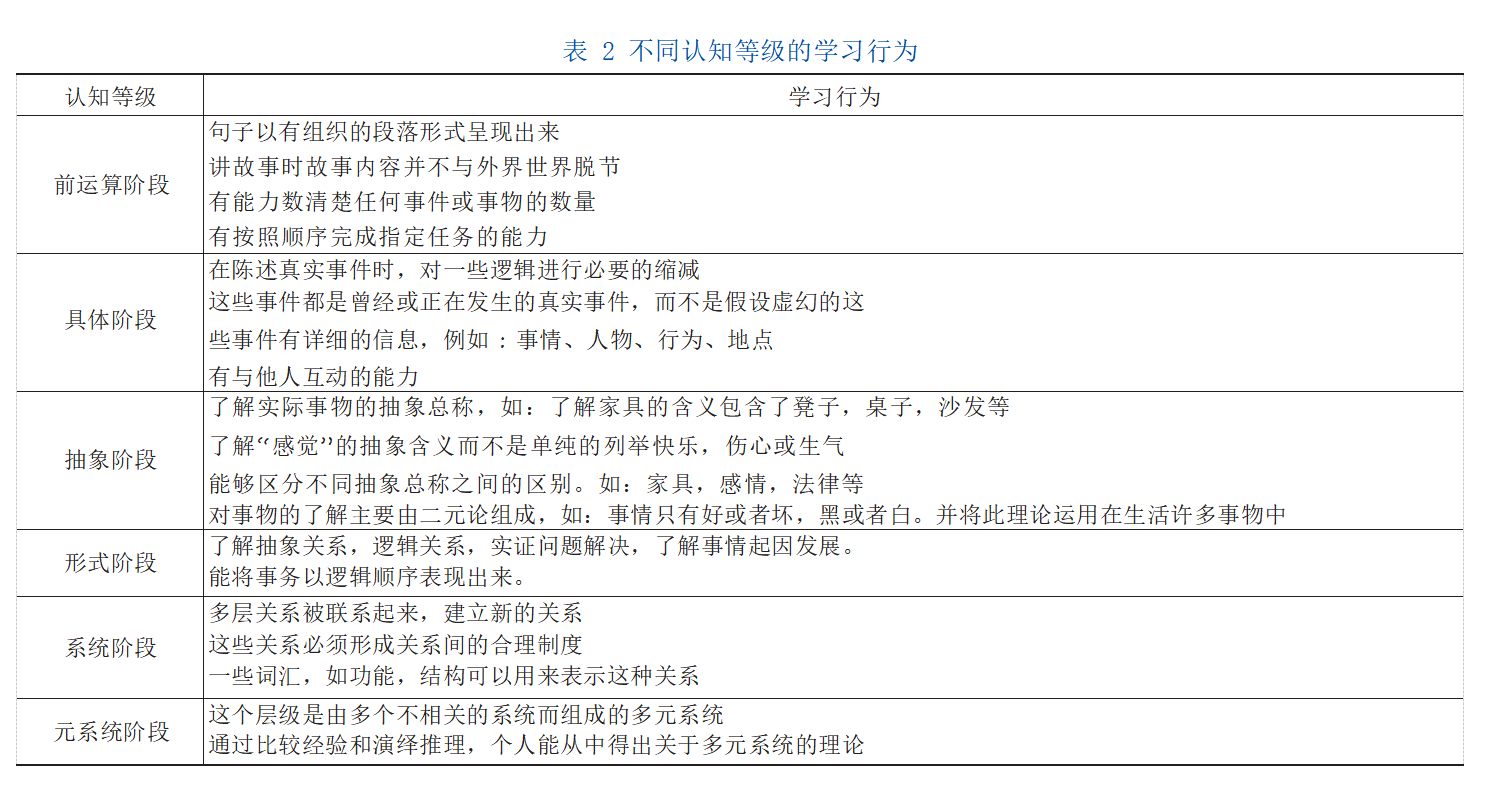
MHC 覆盖了从婴儿到成人阶段的不同认知等级,且对于不同学科而言,过于细化的认知等级将为教学准备带来更大的难度。因此,在设定认知等级的过程中,不同学科的教师可以根据本门课程的特点,在 MHC 的基础上做筛选或者合并,并根据需要达成的目标设定与之对应的学习行为,表 2 列举了部分认知等级下学生的具体行为。
2.为不同认知等级制定学习任务,并及时反馈, 生成个性化学习路径
学习任务是促进深度学习的根本,MHC 将任务要求的行动层次组织进行分类。每个任务都包含许多子任务 (Overton, 1990)[10]。当这些任务按照要求的顺序完成时,学习者们就成功地完成了任务。如今, 借助于信息化系统,我们可以很精确地测量学习者每一个任务的完成情况,当系统检测到学习者在不同等级上的任务完成情况时,自动引导学习者在不同的路径上继续学习。具体做法如图 2 所示。
值得注意的是,除了任务的细化,还需要在不同层次上设置反馈信息:
在低阶认知阶段,此时的任务类型学习者可以立即获得有关他们是否正确的信息。还可以告诉学习者,他们尝试了多少次尝试,尝试次数有限。这个数字可以很高,让学习者解决他们的错误。
除了允许学习者直接访问答案,可以尽可能多地编写解决方案。比如一些课程将提供答案的推导过程,一些课程提供解决问题的一般原则,甚至一旦学习者点击“显示答案”,就会获取新的思路。一些任务类型允许添加提示,以揭示常见的错误。
3.搭建在线学习平台
我们用 moodle 搭建了这样一个学习系统以实施精密教学策略。我们首先将知识分解为非常小的问题和任务,为不同等级设定量表,并对学习者做如下要求:
√ 从系统获取实时的学习表现以强化自身的学习动力;
√ 在回答问题后寻求及时地反馈和解析,以便通过正确答案来强化记忆和学习;
√ 利用系统制定进阶式的学习路径以促进知识的完全掌握和运用;
√ 利用答题系统的试错机制进行大胆猜测,拓展思维的广度和深度。
在这个学习过程中,正如事先设定的认知等级一样,一开始大家都很轻松,并产生了强烈的学习兴趣,每个人都尽力去完成不同阶段的学习任务。随着学习的深入,挑战越来越大,类似游戏中的闯关, 如果参与者正确率没有达到目标频率, 则无法进入下一层次的学习。越到后面,越要综合运用前面的知识来完成复杂的任务。到最后,所有完成学习任务的人都看到了自己的显著进步。
我们回头再来看看这一次批量的深度学习是如何达成的。除了良好的教学理论和教学设计的支持, 在这个过程中,大数据、人工智能技术取代了老师的大部分工作:
√ 收集学生行为及学习表现,了解不同学生的认知阶段;
√ 通过了解学生的认知能力,提供适合不同学生所对应的不同资源;
√ 问题以难度的区分分为不同的部分 ( 最简单的问题放在最前面 ),题目难度最大限度匹配学生的表现和学习能力。
课程结束后,尽管学习者们最后所达到的认知等级有所不同,但都达到了布鲁姆教学目标分类的后四层。我们对学习者进行了访谈,调查他们在这一学习过程中的感受和收获,数据表明,学习者们均表现出较高的学习兴趣和学习成就感。根据访谈结果,我们总结出精密教学提高学生参与度的四个主要原因:
√ 学生能看到自己的进步;
√ 实时得到学习表现能强化学习者的学习动力;
√ 每道小题用时很短;
√ 在学习过程中需要必要的猜测,学生必须积极的思考。
四 小结
本研究提出了信息化环境下促进深度学习的精密教学策略,通过认知等级、学习任务和学习行为构成学习的闭环,并通过具体教学实践引导学习者在 moodle 在线教学平台上展开深度学习,为下一步开展深度学习的评价工作奠定了基础。后续研究将关注深度学习下的评价模式,在基于海量学习数据和人工智能的技术基础之上,构建深度学习的自动化评价框架。
参考文献
[1] 何玲 , 黎加厚 . 促进学生深度学习 [J]. 现代教学 , 2005, 1(5): 29-30.
[2] 郭华 . 深度学习及其意义 [J]. 课程 . 教材 . 教法 , 2016, 36(11):25-32.
[3]何克抗 . 深度学习 : 网络时代学习方式的变革 [J]. 教育研究 , 2018, 39(5): 111-115.
[4]何晓萍 , 沈雅云 . 深度学习的研究现状与发展 [J]. 现代情报 , 2017, 37(2): 163-169.
[5]李洪修 , 李哨兵 . 深度学习下翻转课堂的实施路径设计 [J]. 中国电化教育 , 2017, (7): 67-72.
[6]殷常鸿 , 张义兵 , 高伟 , 等 .“皮亚杰—比格斯”深度学习评价模型构建 [J]. 电化教育研究 ,2019,40(07):13-20.
[7]Coombs, C. H., Dawes, R. M., and Tversky, A. Mathematical psychology: An elementary introduction[J]. Englewood Cliffs, 1970.
[8]Richards, F. A. A general model of stage theory. In Beyond f ormaloperations: Late adolescent and adult cognitive development, Eds [J]. New York: Praeger, 1984(1): 120–140.
[9]Shannon, C. E., and Weaver, W. The mathematical theory of communication[J]. Cham-paign: University of Illinois Press, 1949.
[10]Overton, W. F. Reasoning, necessity, and logic: Developmental perspectives[J]. Lawrence Erlbaum, 1990.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/32440.html