SCI论文(www.lunwensci.com):
摘要:文章根据物流管理专业的特点及差分方程的重要性,提出了学习差分方程的有效学习方法。
关键词:差分方程;物流管理;三步滚动学习方法
本文引用格式:公全英.带领物流管理专业学生学习差分方程的一点经验[J].教育现代化,2019,6(80):300-302.
物流管理专业是经济类学生的重要专业,物流管理简单说就是运用最有效的管理原理和方法,使物流活动达到最优化的专业学科。它涉及经济地理学、系统论信息论、运筹学控制论、最优化理论等,这些理论的基础离不开微积分,差分方程就是微积分非常重要的基础知识之一。而且在物流管理专业考研时,所考数学(三)中也经常出现差分方程的题目。我从自身教学方面探讨一下自己的经验。
一差分方程与微分方程的区别
提到差分方程,自然联想到微分方程,还经常将微分方程和差分方程混淆,这是由于在算法过程中两者有些类似。实际上两者是不同的基础概念,比如在数字信号处理中微分方程涉及了模拟滤波器,差分方程涉及数字滤波器。微分方程和差分方程的第一区别,两者研究对象不同。微分方程研究的是连续函数,差分方程研究的是离散函数。微分方程和差分方程的第二区别,两者研究工具不同,微分方程用导数研究,差分方程用差分研究。微分方程和差分方程的第三区别,两者用途不同。例如前面说的,在数字信号处理中涉及的模拟滤波器应用了微分方程,而差分方程应用于数字滤波器。差分方程的解法还可以来求解递推数列的通项公式,微分方程就无能为力了。

所以有书上说,在某一整数点的导数值是此点差分的逼近近似值。因此,在差分方程编入微积分教材时,编者吴教授将离散数学中的差分方程放在了微积分微分方程的后面。
二学习差分方程的方法
在学习差分方程之前,先让学生把学习微分方程的方法做了以下总结。微分方程学习的方法,用的是“三步滚动学习法”。“三步滚动学习法”,简单地说就是复习,听课,复习的循环使用。差分方程也将使用“三步滚动学习法”,具体使用的过程是这样的。
首先搞清差分方程的章节内容。差分方程是经济数学微积分(吴传生主编)课本中的第十章中第六节至第九节的内容。具体是第六节“差分与差分方程的概念”“常系数线性差分方程解的结构”,第七节“一阶常系数线性差分方程”,第八节“二阶常系数线性差分方程”,第九节“差分方程的简单经济应用”。学生应该先知道差分方程共讲四节内容。
然后每一节都要使用三步滚动法,每一目都要使用三步滚动学习法,每一个知识点都要使用三步滚动学习法。而且每一节每一目每一个知识点还要相互衔接。
接下来用第六节第二目差分方程的概念来做例子。假设已经用“三步滚动学习法”把第六节第一目差分的概念学完了。下面要学习第二目差分方程了。
(一)布置预习
由于时间紧。我们往往一次课就将第一目和第二目以及第三目讲完了。所以第一目和第二目以及第三目的预习,在第十章第五节讲完课后就布置给学生了。因此只以第二目为例,来阐释“预习”。这个预习建立在第一目掌握的基础上来说。学生无论以何种方式何地何时都可以进行,许多优秀的学生都是在吃饭、劳动、走路时,甚至在第五节刚刚宣布下课,他站起走出教室那一刻就开始进入预习状态了。大脑里想到,差分概念学完

然转化为其他两种形式。这时候,心中涌起一种小小的幸福。接着往下想,微分方程中定义了阶的概念:函数的导数最高阶数是微分方程的阶。那差分方程的阶是否是差分的最高阶数呢?看书印证一下,不是。正确定义是:未知函数的最大下标与最小下标的差定义为差分方程的阶。这两种定义是否是一回事呢?细细一想,真不是,比如-2yt=2yt+3t就不算是差分方程,虽然公式中出现了一阶差分,所以自己错了。不过没关系。认识事物就是用自己已有的知识来解释未知的知识,学习就是行走在犯错然后纠正错误的道路上。继续恢复自信往下想。微分方程讲到了通解,差分方程的通解应该有类似定义,果然正确。再拓展到微分方程的初值问题,微分方程的初值问题涉及初值条件和特解的定义。只要把微分方程对应的定义中“微分”改成“差分”即可。到此,第二目预习结束。下面暗示自己听完第二目课后要思考“第三目会是什么呢”?回答:应该具有类似微分方程的解的结构了吧。
(二)讲课过程及注意事项
(1)预备知识的复习。还是以第十章第六节第二目差分方程为例。教师心中当然要列出预备知识。第十章第六节第二目差分方程的预备知识为六点:①微分方程的定义,②函数差分概念公式
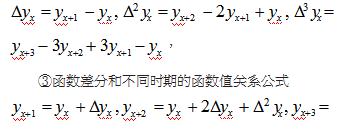
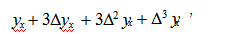
微分方程的阶,⑤微分方程的通解,⑥微分方程的初值条件。预备知识的复习不能简单地罗列给学生,免得无趣或使得学生无措。可以用提问的方式,让学生回答,比如①和④。可以用默写抽查的方式,比如②和③。可以在讲解过程中提出,集体回答,比如⑤和⑥。
占用时间不可过多,一般三分钟,最多五分钟。时间长学生会倦怠,尤其是分化在成绩两极的学生。如果提问,尽量找学习较好的学生来回答,一节省时间,二基本能回答出来,不起冲突,三起到好的榜样作用。默写抽查
尽量照顾到学习排在后面的学生或调皮学生或作业不太认真的学生,以起到督促,提醒,鞭策的作用,当然不
能每次都表现明显,让学生自我贴了标签,起了逆反心理,效果就不好了。
(2)问题的提出。复习完之后就提问一个承上启下的问题。一个好的问题不在于它有多难,但一定要让学生有思考过程、稍加思考就能得到答案,并且能培养一定的能力。还是以第十章第六节第二目差分方程为例。第一个问题是很简单的一句话:差分的概念掌握了,下一步会讲什么呢?学生会简单做思考,这个思考可能就那几秒钟,思考过程大多是这样的:听到问题,回想差分概念,脑中闪现差分定义公式,联想前面为什么讲微分方程,做出回答“差分方程”。不要小看这一句话。只此一句,就可以再现当时无数个数学家们思考抽象出来差分方程的过程,有利于学生抽象思维的培养,有利于学生创造思维的培养,有利于学生自学能力的培养,有利于培养学生对差分方程的兴趣。只此一句,凡是答上来的,就可以给学生带来自信。预习过的学生会坚定继续预习的信心,预习能够培养自学能力。没有预习的学生也会好好往下听,这句话对没有预习的学生起到了一个预习作用,或许某一天他会自觉想去预习,培养了学生的兴趣。听讲的学生回答上来,他会继续好好听讲,没有听讲的学生若回答上来,他会窃喜自己的回答,一下子从跑神状态回到听课。只此一句,就有利于维持我们的课堂秩序。不要小看讲课中类似这种不经意问题的提出。
(3)上课时要求学生遵守课堂纪律。最基本的一定要做到。①不旷课,②不迟到,不早退,③不随便离位走动,④举手说话,⑤不玩手机,⑥尽量做到不跑神。
①②③条学生基本做到,④即便不举手,学生会喊“老师”。难的是⑤不玩手机。第一次上课我就要求把手机放到所有学生认可的地方,而且依据学号,做了所有学生学号对应的纸卡片。微积分经常上课大教室,空很多排位子,取两排即可。我将卡片按学号从小到大放好,然后让学生进教室将手机盖在卡片上,谁没来或手机没放过来一目了然,即放了手机,又点了学生数,一举两得。几次课之后,学生就养成习惯了。为了做到⑥尽量不让学生跑神,使用了随身喇叭,在声音上力求抑扬顿挫感染学生,且声音洪亮让学生不至于劳累,对跑神较严重的就点名一下,甚或到学生身边讲几秒钟。其实给学生在第一节课,就讲明道理,学生会做到自律的。因为学生懂得自律就是自爱,也是爱他人。人人自律,最能体现人人平等。泰戈尔说过:教育的目的应当向人传递生命的气息。我认为作为一名教师,对待学生既要学着讲大道理,也要弯下腰尊重学生、呼唤美好,使学生向善。柴静在《看见》里说过:教育是人与人之间的,也是自己与自己之间发生的事,它永不停止,“就像一棵树摇动另一棵树,一朵云能碰另一多云,一个灵魂唤醒另一个灵魂”。
(4)讲完所有内容之后,①要注意总结本节内容。总结时要言简意赅,重点突出,自成体系,逻辑完整,便于记忆。还是以第十章第六节第二目差分方程为例。可以总结为本节讲了差分方程定义,阶定义,通解定义,初值问题的概念,特解定义。②要布置思考问题:下面将讲什么内容?③要布置复习内容:微分方程解的结构。④要布置预习内容;一般预习下一目或下一节。⑤要布置课后作业。上完课后,学生的课后复习尤为重要。我教给学生的方法是,先不要看书,回忆今天讲课内容,用查漏补缺的方法复习内容。还是以第十章第六节第二目差分方程为例。回忆过程中五个知识点“差分方程定义,阶定义,通解定义,初值问题的概念,特解定义”中忘了“初值问题”,也不要急于看书,先回忆一下自己预习的过程,看一下微分方程的初值问题,实在想不起来再看书。这样的复习,才会事半功倍。然后,做作业做习题。布置的作业一般难度不大,基本能够很快完成。不会的习题,不要急于看答案,先放几天,下次复习时再做,或与同学老师讨论,或许就做出来了。下面就滚动到下一目三步学习了。至此,用“三步滚动学习法”就带领学生把差分方程学习完了。
学习差分方程期间,还有一个重要学习方法,就是对照类比法。常系数线性差分方程解的结构对照类比常系数线性微分方程解的结构。二阶常系数线性差分方程对照类比二阶常系数线性微分方程。
特别提提二阶常系数线性差分方程对照类比二阶常系数线性微分方程。
(1)二阶常系数线性差分方程和二阶常系数线性微分方程都是用所对应齐次方程的通解加上自己一个特解来求自己通解;
(2)二阶常系数线性差分方程和二阶常系数线性微分方程在求自己所对应齐次方程通解时,都是用的一元二次特征方程及一元二次特征方程的根的情况来讨论所对应齐次方程的通解情况;
(3)当二阶常系数线性差分方程和二阶常系数线性微分方程为非齐次方程时,都是讨论方程中有关自变量函数项的情况,并结合自己所对应特征方程的根的情况来写出自己特解的待定特解,用待定系数法求出自己这种情况下的特解。
对照类比法在整个数学学习体系中也是一个重要的学习方法。
三让学生了解差分方程在物流管理专业考研
(三)中的题目
告知学生差分方程在物流管理专业考研(三)中的题目题数不用多目的,让学生重视学习差分方程即可。为什么不用多呢,原因有两个。1.面向的是所用学生,每个人志向不同,讲多会误会功利心太重,引起学生普遍反感。2.即便打算考研,讲多了战线拉得太长也不利于考研。
告知题目一定要准确。比如在2017年和2018年全国硕士研究生考试数学(三)第二大题填空题中,就考到了差分方程通解的求解。题目写下来让学生回去试。
 四 在差分方程的学习中注意发现美
四 在差分方程的学习中注意发现美
差分方程体现的是数学思维逻辑,我们知道,数学是思维的体操。体操的美,大家有目共睹。由于差分方程是脑力劳动和体力劳动的结合,所以差分方程还体现了劳动美。爱学差分方程,不怕苦,不怕累,爱与同学老师讨论,态度温和,这里面又体现了心灵美,行为美,语言美。差分方程及解的形式是美的,尤其是差分方程的特征方程一出现,那美妙的一元二次方程,犹如美丽的少女,惊艳了爱学数学的人的芳心,使本来一筹莫展的学子一下子找到了解题的方法;犹如春天里一场及时的小雨,洗去空气中的雾霾,让花花草草露出本真的纯美,涤荡学子在差分学习遇到困难时愁闷的心灵。
物流管理专业学生只要掌握了差分方程的学习方法,用一颗静美的心,就能把差分方程学好。世上无难事,只怕有心人。
参考文献
[1]吴传生.经济数学——微积分[M].北京:高等教育出版社,2003.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/29354.html