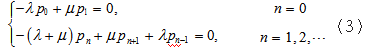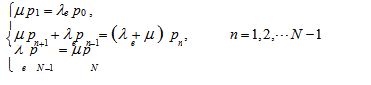SCI论文(www.lunwensci.com):
摘要:针对数学建模课程中排队模型的稳态概率方程建立问题,提出了概率流守恒的方法,帮助学生快速、准确地写出方程组表达式,从而得到判断排队系统服务优劣的各项数量指标。
关键词:排队论;平均到达率;平均服务率
本文引用格式:李伟,等.排队问题中稳态概率方程的建立技巧[J].教育现代化,2019,6(71):245-247.
Technique to Build Stationary Probability Equations for Query Problems
LI Wei1,ZHAO Jun-feng2
(1.School of Mathematics and Statistics,Xidian University,Xi'an,China;2.School of Science,Northwestern Polytechnical University,Xi'an,China)
Abstract:Regarding the problem of how to build the stationary probability equations for queue model when teaching the course of mathematical modeling,a technique based on the conservation of probability flow is proposed,which can help students write out the expression of stationary probability equations fast and precisely,in order to obtain the indexes to identify the service of a queuing system.
Key words:Queuing theory;Average arrival rate;Average service rate
一引言
近些年来,随着教育教学改革在全国各大高校的广泛开展,数学建模课程越来越受到广泛关注,因为该课程是有效培养大学生实践能力、创新能力和合作能力的最佳载体,是传授知识、提高学生综合素质的最佳途径。作为数学建模课程的授课教师,在新形势下的教学过程中,也在不断地适应时代发展,在教学内容和教学方式上进行相应的改进和提高。
排队是日常生活中常见的一种现象,大家熟悉的比如银行办理业务、医院看病诊治,零部件依次加工等。鉴于排队现象的普遍性,与其相关的排队论模型也成为数学建模课程的必要内容,在理论上成为研究系统随机聚散现象和工作过程的有力工具。它适用于一切服务系统[1,2],包括通信系统、计算机系统、航道管理、交通管理、物流管理等多个领域。排队模型在数学上属于随机优化的分支,经常出现在高校研究生随机过程这门课程的必修内容之中[3,4],在理论上涉及概率论、数理统计、优化和随机过程等基础知识,是一门实用性广但理论比较深入的学科。即便如此,在近些年来的数模竞赛中,排队模型以及排队理论也经常出现在面对广大本科生的赛题中。例如,2009年中国大学生数模竞赛题目[5]“眼科病床安排”就是利用排队模型进行解决。
一般情况下,排队论模型是数学建模课程的必学内容之一,几乎每个数模老师都会向学生详细介绍排队模型的理论和应用。然而,由于排队模型背后的理论支撑涉及概率论、随机过程、优化等数学知识,使得学生在课堂上顺利领会排队模型的要领具有一定的难度。如何能让学生快速准确的建立排队模型中的稳态概率方程,成为数学建模老师在授课过程中必须重点考虑的内容之一。本文将针对该课程中排队模型的授课问题,谈一谈建立相应的稳态概率方程的技巧和方法。
二排队模型的预备知识
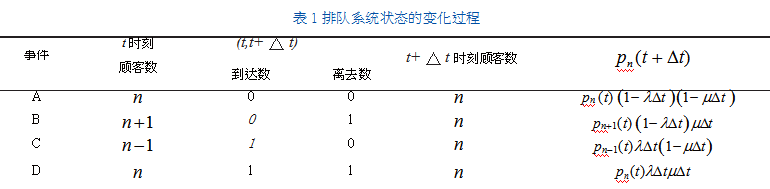
首先,考虑最具有代表性的排队情形[6](M/M/1模型),即顾客是源源不断地到来,形成一股泊松流,只有一个服务台提供服务,系统内队长没有限制,先到先服务。假设排队系统中“顾客”的到达相互独立,且服从参数为的泊松分布,服务台的平均服务率为常数μ,且服从负指数分布。记t时刻排队系统中有n个顾客的概率为pn(t),则t+△t(△t→0)时刻系统中n个顾客的概率为pn(t,t+△t),并且△t时间间隔内系统的状态变化可用表1进行描述。
显然,在(t,t+△t)内,ABCD四种情况是相互独立的事件,均可能发生,因此,t+△t时刻系统内有n个顾客的概率为:

可以看出,上面的微分方程刻画了不同时刻排队系统的状态,对应的解是瞬时情况的解。但在实际生活中,大家更关心的是服务机构工作环境稳定后的运营情况和服务质量,即稳态情况,因此令t,则有
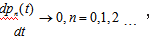
此时方程组(2)中的系统状态与时间无关,可改写为以下稳态概率方程组:
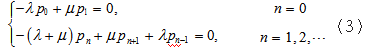
对方程组(3)进行求解,可依次得到pn的递推公式,之后应用离散型随机变量的数学期望公式可分别确定排队系统各个运行指标如队列长、排队时间等的计算公式[3]。显然,在排队问题中,稳态概率方程组(3)的有效、正确的建立至关重要,影响到后面所有数量指标的计算和结果。然而,回顾整个分析过程,学生必须依次分析系统状态的动态变化过程,穷举出所有互不相容事件,列出表1,并进行微分转换等数学上的处理,才有可能建立如(3)式的稳态概率方程,这对绝大多数的本科学生特别是非数学专业的学生来说都是比较困难的,中间一旦出错,整个排队系统的判断也会跟着出错。因此,如果能够给出一个方便、简单、容易理解、又容易操作的方法帮助学生建立稳态概率方程,将会是一件非常有意义而实用的事情。
三 稳态概率方程建立技巧
如何能够简单正确地写出稳态概率方程组?关键的技巧是画出排队问题系统状态的转移图。方法如下:以标准的排队模型M/M/1为例,顾客的到达服从泊松分布,服务机构的服务时间服从负指数分布,只有一个服务台工作,排队系统内的顾客数量是无限的,排队系统外的顾客源也是无限的,先到先服务。如果这样,用整数 0,1,2, 等加方框表示排队系统内的顾客数,用常数 λ 表示平均到达率,用常数 μ 表示平均服务率,则可认为系统以 λ 的概率从状态 0 转移到状态 1,即刻画了顾客到达的规律;反之,系统以 μ 的概率从状态 1 转变为状态 0,即刻画了服务台服务顾客的规律,见图 1。现在将这些整数 0,1,2... 对应的系统状态想象成液体流过的面积,将到达率 λ 或服务率 μ 想象成液体的流速,则系统的状态与到达率或服务率的乘积就类似于某种液体按照一定的流速通过某个面积的流量。而流量是守恒的,即流入 = 流出。因此根据概率流守恒,我们只需在每个状态处找到流出量和流入量,让两者守恒相等即可。观察图1中整个状态转移图,除了状态0外,每个状态都对应两个流入,两个流出,即状态1,2,...有统一的转移特征,可以写出一个通式。例如在状态n处,流入的部分包括n-1处的截面和流速λ形成的流量pn1以及n+1
处的截面和流速μ形成的流量μpn+1,所以流入总量为pn1pn1。反之,流出的部分包括n处的截面和流速λ形成的流量λpn以及n处的截面和流速μ形成的流量μpn,所以流出总量为()pn,当流量守恒时,我们有pn1pn1()pn,即得方程组(3)中的下式。在状态0处,只有一个流入和一个流出,所以需要单独处理,但方法和思想一致。根据流量守恒,流入量为μp1,流出量为λp0,即μp1=λp0,得到方程组(3)中的上式。掌握了这种方法,对于其他类型的排队问题,稳态概率方程的确定就可依次写出。现在考虑M/M/1/N/问题,即顾客的到达服从泊松分布,服务机构的服务时间服从负指数分布,只有一个服务台工作,排队系统内的顾客数量是有限的N个,排队系统外的顾客源仍然是无限的,先到先服务,见图2。根据概率流守恒方法,流入等于流出的规律,对应的稳态概率方程应该有三个,0 状态和 N 状态都只有一个流入和流出,所以要单独列出方程,其余都是两个流入流出,可以写出通式,所以有其他的多服务台模型也可按照这样的稳态概率方程建立技巧分别写出,之后求出各数量指标去衡量服务机构的服务质量和最优配置等问题。
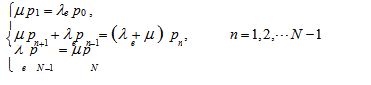 四结论
四结论
针对排队问题中稳态概率方程难以建立、理论复杂等特点,本文提出了一种概率流守恒方法,根据流入量等于流出量的思想,帮助学习数模的学生快速、准确地建立稳态概率方程,为之后确定排队系统数量指标的计算提供了保障。本文提出的方程建立技巧,简单易懂,容易操作,对数学建模爱好者或应用者具有很好的指导作用。
参考文献
[1]姜启源,谢金星,叶俊.数学模型[M].北京:高等教育出版社,2013:18-20.
[2]韩中庚.数学建模方法及其应用[M].北京:高等教育出版社,2009:258-277.
[3]http://www.mcm.edu.cn/html_cn/node/50a7a9fc36c5ce6fd242dbbc1da5878e.html.
[4]冯海林,薄立军.随机过程—计算与应用[M].西安电子科技大学出版社,2012:184-202
[5]张卓奎,陈慧婵.随机过程[M].西安电子科技大学出版社,2003:227-248.
[6]陈东彦,李冬梅,王树忠.数学建模[M].北京:科学出版社,2013:305-333.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/28301.html

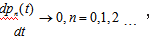 此时方程组(2)中的系统状态与时间无关,可改写为以下稳态概率方程组:
此时方程组(2)中的系统状态与时间无关,可改写为以下稳态概率方程组: