SCI论文(www.lunwensci.com):
摘要:本文运用结构方程方法,对44种影响数学建模能力的因素进行分析,发现学生对数学建模基本过程的了解这一影响因素对数学建模能力的各个方面影响程度都非常大,且都为正向影响;直接影响模型的有8个因素,其中6个为正向影响;直接影响算法的有11个因素,其中6个为正向影响;直接影响结果的有14个因素,其中9个为正向影响;直接影响论文的有9个因素,其中5个为正向影响;直接影响检验的有13个因素,其中8个为正向影响;直接影响综合能力的有8个因素,其中5个为正向影响;直接影响获奖级别的有8个因素,其中5个为正向影响。
关键词:数学建模能力;结构方程方法;影响因素
本文引用格式:刘璐,等.师范院校本科生数学建模能力影响因素研究[J].教育现代化,2019,6(70):264-267.
数学建模可以在解决实际问题和数学理论和方法之间搭建桥梁,为扩大学生知识量、提高创新思维和创新能力提供了极好的舞台,是培养创新人才的有效途径,现今各大高校重视数学建模能力。[1]通过对本科生数学建模能力的有关研究,笔者发现当前大家对于数学建模能力的主要影响因素没有达成统一认识,因此本文将对此进行研究。
一研究假设与模型构建
(一)研究假设
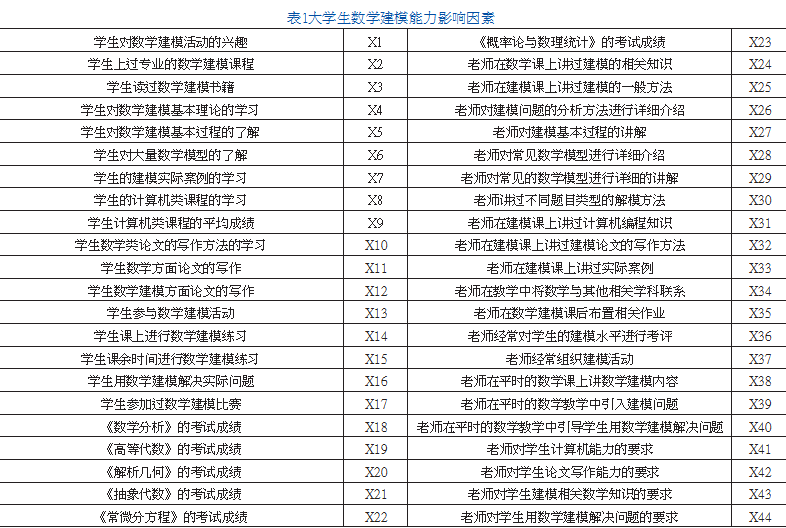
笔者对近20年有关培养大学生数学建模能力的文献进行整理,有44种提及频率在50%以上的影响因素,分为学生方面和教师方面两大类,以此作为接下来研究的自变量X1、X2……X44(见表1)。根据大学生数学建模竞赛的评分标准,将学生的数学建模能力分为模型、算法、结果、论文、检验5个部分,作为接下来研究的因变量Y1、Y2、Y3、Y4、Y5;数学建模综合能力为因变量Y;学生在大学生数学建模竞赛的获奖级别为因变量Z。基于以上内容,提出以下假设:
H1:X1……X44都对Y1有直接影响。H2:X1……X44都对Y2有直接影响。H3:X1……X44都对Y3有直接影响。H4:X1……X44都对Y4有直接影响。H5:X1……X44都对Y5有直接影响。H6:X1……X44都对Y有直接影响。H7:X1……X44都对Z有直接影响。
(二)模型构建
由于大学生数学建模能力的影响因素与建模能力之间涉及的变量比较复杂,难以直接量化,因此选择结构方程方法进行分析。结构方程模型分析是用变量的协方差矩阵来分析变量间关系的一种统计方法,适用于变量间复杂关系的分析,比一般传统方法更适合该问题。[2]本文使用AMOS22.0来完成模型的构建。
二问卷调查与信度检验、建模能力得分
(一)问卷调查
根据前面所提到的44个影响因素,编写相对应的具有44道题目的问卷,题目全部采用李克特的5点量表法,将问卷发放给2018年参加大学生数学建模竞赛的同学,共发放90份,一周后回收86份有效问卷,回收率95.56%,符合统计学要求。
(二)信度检验
为保证本次调查样本的可信度,笔者对问卷进行了信度检验,根据Alpha系数,分析后的结果均在0.75以上,满足条件。
(三)建模能力得分
邀请专业的建模教学组对学生们参加建模竞赛的论文按照模型、算法、结果、论文、检验五个部分进行打分,以每个部分的得分来对学生数学建模能力进行量化,将数值用于接下来结构方程分析中。
三模型实证分析
(一)数学专业本科生数学建模能力——模型
假设所有的自变量X都对因变量“数学专业本科生数学建模能力——模型(Y1)”有影响,经过修正后的模型拟合指数为(见表2):
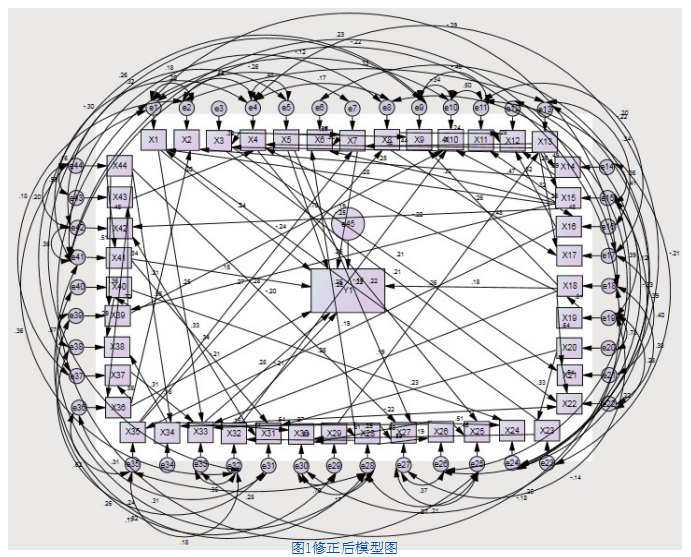
修正后模型结构如图1所示。
由图1可以看出,共有8个自变量直接影响因变量Y1,分别是X1,X5,X7,X18,X32,X33,X36,X41,它们对Y1直接影响的路径系数分别为0.24、0.70、-0.19、0.18、-0.21、0.28、0.21、0.15。
其中,X1、X5、X18、X33、X36、X41对Y1产生了正向影响;X7、X32对Y1产生了负向影响;X5对Y1的影响程度较大;此外还有间接影响的自变量。
(二)数学专业本科生数学建模能力——算法
假设所有的自变量X都对因变量“数学专业本科生数学建模能力——算法(Y2)”有影响,修正后的模型拟合指数为(见表3):
修正后模型结构类似图1。
由修正后模型结构图可以看出,共有11个自变量直接影响因变量Y2,分别是X1、X5、X9、X15、X17、X19、X21、X25、X36、X39、X43,它们对Y2直接影响的路径系数分别为0.23、0.56、0.24、-0.14、-0.15、0.23、-0.17、0.23、-0.15、-0.30、0.21。
其中,X1、X5、X9、X19、X25、X43对Y2产生了正向影响;X15、X17、X21、X36、X39对Y2产生了负向影响;X5对Y2的影响程度较大;此外还有间接影响的自变量。
(三)数学专业本科生数学建模能力——结果
假设所有的自变量X都对因变量“数学专业本科生数学建模能力——结果(Y3)”有影响,修正后的模型拟合指数为(见表4):
修正后模型结构类似图1。
由修正后模型结构图可以看出,共有14个自变量直接影响因变量Y3,分别是X1,X3,X5,X7,X17,X19,X28,X32,X33,X36,X37,X44,X39,X41,它们对Y3直接影响的路径系数分别为0.31、0.18、0.48、-0.17、-0.15、0.15、0.16、-0.27、0.29、-0.32、0.25、0.27、-0.28、0.19。其中,X1、X3、X5、X19、X28、X33、X37、X44、X41对Y3产生了正向影响;X7、X17、X32、X36、X39对Y3产生了负向影响;无影响较大的自变量;此外还有间接影响的自变量。
(四)数学专业本科生数学建模能力——论文
假设所有的自变量X都对因变量“数学专业本科生数学建模能力——论文(Y4)”有影响,修正后的模型拟合指数为(见表5)
修正后模型结构类似图1。
由修正后模型结构图可以看出,共有9个自变量直接影响因变量Y4,分别是X5,X14,X16,X17,X21,X27,X29,X34,X38,它们对Y4直接影响的路径系数分别为0.61、-0.22、0.16、-0.25、0.15、-0.23、0.31、0.19、-0.26。其中,X5、X16、X21、X29、X34对Y4产生了正向影响;X14、X17、X27、X38产生了负向影响;X5对Y4的影响程度较大;此外还有间接影响的自变量。
(五)数学专业本科生数学建模能力——检验
假设所有的自变量X都对因变量“数学专业本科生数学建模能力——检验(Y5)”有影响,修正后的模型拟合指数为(见表6):
修正后模型结构类似图1。
由修正后模型结构图可以看出,共有13个自变量直接影响因变量Y5,分别是X1,X5,X9,X15,X16,X17,X21,X33,X34,X35,X40,X41,它们对Y5直接影响的路径系数分别为0.13、0.27、0.28、-0.27、0.29、-0.18、0.26、0.35、0.14、-0.22、-0.21、-0.22、0.23。其中,X1、X5、X9、X16、X21、X33、X34、X41对Y5产生了正向影响;X15、X17、X35、X36、X40对Y5产生了负向影响;无影响较大的自变量;此外还有间接影响的自变量。
(六)数学专业本科生数学建模综合能力
假设所有的自变量X都对因变量“数学专业本科生数学建模综合能力(Y)”有影响,修正后的模型拟合指数为(见表7):
修正后模型结构类似图1。
由修正后模型结构图可以看出,共有8个自变量直接影响因变量Y,分别是X1、X5、X17、X18、X33、X35、X39、X41,它们对Y直接影响的路径系数分别为0.23、0.59、-0.15、0.27、0.22、-0.23、-0.20、0.19。其中,X1、X5、X18、X33、X41对Y产生了正向影响;X17、X35、X39对Y产生了负向影响;X5对Y的影响程度较大;此外还有间接影响的自变量。
(七)全国大学生数学建模竞赛获奖级别
假设所有的自变量X都对因变量“全国大学生数学建模竞赛获奖级别(Z)”有影响,修正后的模型拟合指数为(见表8):
修正后模型结构类似图1。
由修正后模型结构图可以看出,共有8个自变量直接影响因变量Z,分别是X1,X5,X9,X32,X33,X36,X38,X41,它们对Z直接影响的路径系数分别为0.24、0.54、0.17、-0.27、0.49、-0.18、-0.17、0.20。其中,X1、X5、X9、X33、X41对Z产生了正向影响;X32、X36、X38对Z产生了负向影响;X5对Z的影响程度较大;此外还有间接影响的自变量。
四结论与建议
(一)培养学生对数学建模活动的兴趣
研究结果显示,学生对建模活动的兴趣对数学建模能力的模型、算法、结果、检验、综合能力、获奖级别方面都有较为明显的影响,因此要注重培养学生对建模活动的兴趣。首先,学校可以加大数学建模的宣传力度,开设校内数学建模社团;其次,设立奖励制度,对参与数学建模获奖的同学给予物质和精神上的鼓励,例如优先评优评奖、优先考虑研究生保送等等。
(二)加强学生对数学建模基本过程的了解
由研究结果发现,学生对数学建模过程的基本了解这一影响因素,对数学建模能力的五个方面、综合能力、数学建模竞赛获奖级别都有正向的影响,尤其对模型、算法、论文、综合能力、获奖级别的影响显著,路径系数都在0.5以上。因此教师应着重加强学生对数学建模基本过程的了解,在建模课上讲解专业的数学建模基础知识和理论、数学建模过程、数学建模常用模型及衍变,打造专业的数学建模体系;将建模实践作为教学的重要环节,不仅进行课后练习,还要上机实习,在实验课程中学生可以练习建立数学模型。[3]
(三)增加数学建模案例的讲授
研究结果显示,教师在数学建模课上增加案例的讲授,可以有效提高学生数学建模能力的模型、结果、检验、综合能力、获奖级别。对此,教师在选取案例时,要选择贴近学生生活的、新颖有趣的案例,引起学生好奇心和兴趣,在教学中要合理地将数学建模的思维、方法、过程引入到课案实例中;[4]另外,要多增加一些经典案例。
(四)提高对学生计算机能力的要求
研究结果显示,教师提高对学生计算机能力的要求,对学生的数学建模能力的模型、结果、检验、综合能力、获奖级别都有较为明显的正向影响。对此,教师可以课下布置编程作业定期上交;定期进行测评;增加上机实验课的次数,提高学生的计算机编程能力。
(五)适当减少学生参加数学建模比赛次数
研究结果显示,学生参加数学建模比赛的次数对数学建模能力的算法、结果、论文、检验、综合能力都有较小的负向影响。因此教师要考虑适当减少学生的参赛次数。
参考文献
[1]贾秀利.浅谈如何提高大学生的数学建模能力[J].吉林省教育学院学报(中旬),2013,29(06):58-59.
[2]杨帆,袁文,佟巍.大学生学术不端影响因素的结构方程模型研究[J].教育教学论坛,2019(15):44-46.
[3]朱建青,谷建胜.数学建模能力与大学生综合素质的培养[J].大学数学,2013,29(06):83-86.
[4]马书红.基于数学建模的应用型人才培养途径探讨[J].经济研究导刊,2017(07):125-126.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/28202.html