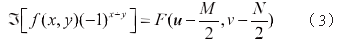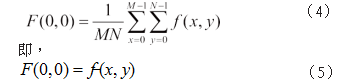SCI论文(www.lunwensci.com):
摘要:傅里叶变换是一种重要的信号分析工具,在数字图像的处理和分析中具有十分重要的地位。本文简述了针对图像处理的二维离散傅里叶变换的基本原理和概念,并对频谱中心化及频谱原点的物理意义两个知识点,结合科研案例,进行了讲解和分析。采用案例讲解的方法,使得枯燥费解的知识点变得通俗易懂,加强了学生对图像傅里叶变换的理解,提高了学生对学习数字图像处理中频域处理和分析的积极性,且对科学研究有了初步的认识,为以后图像处理技术的应用及研究打下基础。
关键词:图像处理;傅里叶变换;案例讲解
本文引用格式:林冬梅,等.案例讲解图像傅里叶变换[J].教育现代化,2019,6(70):211-214.
自数字图像处理起源于20世纪20年代以来,图像处理技术的需求与日俱增。数字图像处理是实用性很强的学科,许多处理算法都具有实际应用背景[1]。图像处理的应用已经渗透到工程领域、工业生产、国防军事、医疗保健、遥感技术、气象预报、航空航天以及科学研究中,在国计民生及国民经济中发挥着越来越大的作用[2]。目前,图像处理科学已成为工程学、计算机科学、信息科学、统计学、物理、化学、生物学、医学甚至社会科学等领域中各学科学习和研究的对象[3]。因此,图像处理类课程在高等学校中普遍开设。它既是电子信息科学与技术、通信工程、计算机科学与技术、生物医学工程、遥感科学与技术等本科专业的必修课程,也是模式识别与智能系统、信号与信息处理、检测技术与自动化装置、电路与系统、机械制造及其自动化等研究生专业的选修课程。
传统的图像处理方式往往适合在时域对图像进行处理分析,而与傅里叶变换相结合便使图像处理技术得以在频域进行[4]。利用离散傅里叶变换的时域与频域分析方法,可解决大多数图像处理问题,因而离散傅里叶变换在图像处理领域得到了极为广泛的应用,涉及到图像的去噪、滤波、增强、压缩、特征提取、复原、卷积、识别、重构和描述等[2-7]。因此,傅里叶变换对于图像在频域的处理至关重要,是频域图像处理的预处理。它是图像处理课程内容的重要组成部分,只有掌握了该部分内容,才能更好地理解和掌握频域图像处理分析方法。
用傅里叶变换分析处理图像信息有许多优点,然而,频域分析要求将思维方式从时域或空域转变为频域[8],该部分内容涉及到繁杂的公式推导及计算,枯燥乏味,造成教师讲解困难、学生理解不深入等问题。部分学生虽然会应用傅里叶变换来进行图像处理和分析,但是不理解其中的物理含义,学习效果欠佳,导致学生不感兴趣。如何将该部分内容形象地讲解,是授课教师所要解决的问题之一。本文结合科研中的实际问题,采用案例讲解傅里叶变换中的知识点,将复杂的问题简单地呈现出来,通俗易懂,使学生能很好地掌握,且印象深刻。
一图像的傅里叶变换
一幅尺寸为M×N像素的图像f(x,y),其离散傅里叶变换F(u,v)由式(1)给出[3]:

等式(1)和(2)构成了图像的二维离散傅里叶变换对。变量u和v是变换分量或频率分量,x和y是空间分量或图像变量。根据傅里叶变换公式(1)可知,F(u,v)为复数,提取其幅值就可以得到图像信号f(x,y)在各个频率点(u,v)上的强度。
利用傅里叶变换的平移特性及指数的性质[3],很容易得到:
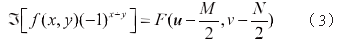
等式(3)说明,用(-1)x+y乘以f(x,y),进行傅里叶变换,可将F(u,v)的原点从(0,0)平移到频率坐标下的(M/2,N/2),即频率坐标下的中心点,实现了频谱中心化。因此,傅里叶变换频谱图的中心区域代表低频分量,从中心越往外,频率越高。对于一幅图像,低频分量对应着空间域上变化比较缓慢的信号,高频分量对应着空间域上变化比较剧烈的信号。空间域上变化比较剧烈的信号主要集中在不同景物的边界上或灰度级的突变(如噪声),反映图像的细节;而空间域上变化比较缓慢的信号主要集中在边界内部的非边界景物信息之中,反映图像的概貌。通常来说,一幅图像中,缓慢变化区域较多,而剧烈变化的信号较少。因此,在原傅里叶变换频谱图中,四角区域较亮,中心区域较暗;而在中心化后的傅里叶变换频谱图中,中心区域较亮,四周区域较暗,如图1所示。上述结论反映了图像中低频信息较多、高频信息较少的事实。
从傅里叶变换公式(1)可得到(u=0,v=0)的变换值为:
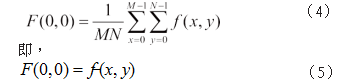
也就是说,图像f(x,y)变化最慢的频率成分(u=0,v=0),等于图像的灰度平均值。
上述结论在空间域和频域相结合的图像处理和分析中,极为有用。为了更好地理解和掌握该知识点,结合科研中的实际问题,进行案例讲解。
二 知识点案例讲解
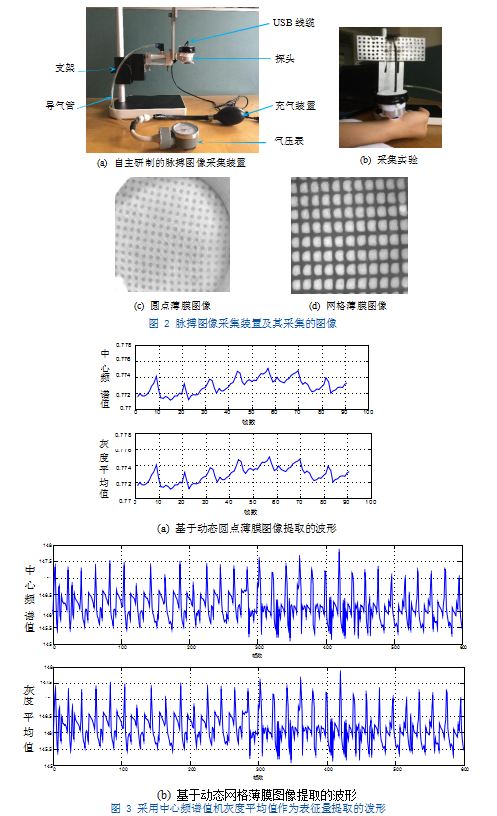
图2(a)所示为自主研制的脉搏图像采集装置,其主要部分为传感探头。探头腔体采用铝合金材质制成,顶端用塑料盖密封,塑料盖内侧粘有摄像头及LED光源,探头底部用印有标志图案的柔性薄膜密封。通过导气管向探头充气使薄膜微微鼓起,将其触压于手腕桡动脉处(如图2(b)所示),模仿中医师切脉,血管壁的搏动便通过薄膜的形变及运动呈现出来。摄像头连续采集动态薄膜图像(图像与薄膜标志图案类型有关,如图2(c)和2(d)所示),动态薄膜图像中便包含了桡动脉的运动信息。因此,通过处理分析动态薄膜图像,便可得到脉搏信息。下面采用两种方法对动态薄膜图像进行处理分析:
方法1:将连续时间段内采集的动态薄膜图像,逐帧进行傅里叶变换,频谱中心化后,取每帧图像的中心频谱值作为表征量,提取波形。方法2:对于连续时间段内采集的动态薄膜图像,取每帧图像的灰度平均值作为表征量,提取波形。
采用Matlab编程实现上述处理。在进行傅里叶变换及求灰度平均值之前,图像数据被转换成了double类型。对两段不同图案、不同帧数的动态薄膜图像,均用上述两种方法进行了处理,结果如图3所示。从波形图可知,两种方法所得波形在数值上及形状上均一致。波形反映了脉搏搏动趋势,进一步处理分析,便可实现脉搏波的提取,该内容不在本文讨论。
在计算机中使用傅里叶变换时,u的范围为(1,2,…,M),v的范围为(1,2,…,N),频谱中心化后的实际变换中心为(M/2+1,N/2+1)。上述两种处理方法所得波形一致的结果,说明了如下两个问题:
(1)傅里叶变换频谱中心化后,将其原点从(0,0)平移到了(M/2+1,N/2+1),即F(0,0)=(M/2+1,N/2+1);
(2)任意一幅图像的变化最慢的频率成分,等于图像的灰度平均值,即F(0,0)f(x,y)。
也即,上述实验案例很好地验证了第2节内容中提到的两个知识点。通过案例讲解的方法,使得该知识点形象地呈现出来,降低了难度,易于学生理解和掌握,提高了学生的学习兴趣。对于图像傅里叶变换中的其他知识点,也可以采用类似的案例法进行讲解。
三结束语
数字图像处理技术是现代社会应用广泛的计算机处理技术,傅里叶变换是图像处理技术中一种极为重要的算法和工具,而案例讲解法的运用能够提高图像处理课程的教学质量。本文通过将图像傅里叶变换中的关键知识点融入实际的科研实验中,源于教材而又高于教材,充分调动了学生的学习兴趣,使学生深刻地理解图像傅里叶变换的概念和意义,提高学习图像处理中频域分析的积极性。对于图像处理课程的其他知识点及其他课程,教师也可以采用类似的方法,将科研实验案例应用到日常教学中,帮助学生步巩固和加深对理论知识的理解,提高学习效率,让学生对科学研究有初步的认识,为以后对知识点的应用及相关研究打下良好的基础。
参考文献
[1]孙燮华.数字图像处理——原理与算法[M].北京:机械工业出版社,2010.
[2]阮秋琦.数字图像处理基础[M].北京:清华大学出版社,2009.
[3]冈萨雷斯等著,阮秋琦等译.数字图像处理(第三版)[M].北京:电子工业出版社,2011.
[4]王丹.傅里叶变换在图像处理中的应用[J].科学与信息化,2018,4月下:9,11.
[5]李俊山,李旭辉.数字图像处理[M].北京:清华大学出版社,2007.
[6]马晓凯,付禹.浅谈傅里叶变换在图像处理中的应用[J].科技资讯,2018,8:80-81.
[7]朱虹.数字图像处理基础[M].科学出版社,2005.
[8]朱亚培,龙祖强,刘灿.傅里叶变换在数字图像处理中的教学方法探讨[J].轻工科技,2016,(2):165-166.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/28139.html