SCI论文(www.lunwensci.com):
摘要:三重积分的计算是教学中的难点和重点。本文结合教学实践,归纳了三重积分的降维解法,避免利用积分区域的立体图去计算三重积分。
关键词:三重积分;投影法;截面法;柱坐标法;球坐标法
本文引用格式:程文韬.三重积分降维解法研究[J].教育现代化,2019,6(65):166-168.
三重积分是高等数学[1]和数学分析[2]中的重要难点之一,具有很重要的实际应用价值。怎样让学生快速、简单、容易地求解三重积分是重要的教学过程。
三重积分解法一般可分为投影法、截面法、柱坐标法、球坐标法。不同的方法都有特定的适用场合,关键都需要利用积分区域Ω的立体图将三重积分化为累次积分,但这相对需要学生要有较强的空间想象能力,很多时候由于Ω的界面比较复杂或者立体图难以画出,从而导致学生无法很好地掌握三重积分的解法。由于平面图形容易想象,本文就是不通过Ω的形状,通过降维方法来计算三重积分,避免利用Ω的立体图,仅需要平面图形相关知识掌握即可去求解三重积分。
一 投影法
投影法又称”先一后二”法,一般是按”z→y→x”顺序进行积分。日常教学过程中要求根据区域Ω的立体图来进行计算。但有时很多曲面很难画出,如z=xy等。这里将给出降维投影法的具体步骤:
第一步 : 将积分区域边界方程整理为两个部分 :
第三步 : 在投影区域 Dxy 上判断 f(x,y) 和 g(x,y)大小,大者记为曲顶方程z=z2(x,y),小者记为曲底方程z=z1(x,y).根据这三个步骤,就可以将三重积分转
化为 Dxy 上的二重积分 :
注1.降维投影法也是有使用条件,题干中对应的若干边界方程仅两个含有z的方程,且z比较容易显示求出,同时,在投影区域Dxy上比较容易判断两个含z的表达式大小关系。其实,多数情形下的三重积分都满足此条件。
二截面法
截面法又称”先二后一”法,同时,一般还需要满足以下条件:一,被积函数f(x,y,z)中至少缺少两个变量。二,平行于所缺变量的平面去截积分区域Ω所得截面面积比较容易求出。这里也给出截面法的具体步骤:
第一步:首先确定z的取值范围z∈[z1,z2].
第二步:将积分区域边界方程含z的部分当成常数和不含z的部分所对应的曲线在平面坐标系围成的封闭区域即为截面区域 Dz( 其面积为 SD) 根据这两个步骤,就可以将三重积分化为Dz上的定积分

质实际上就是将投影法中的投影区域Dxy用极坐标形式表示。因此,投影区域当为圆域,圆环域及其一部分时,可以考虑使用柱坐标法。且体积微元满足

注2.尤其当Dzr区域表达式和θ无关时候,按照上述步骤会容易计算三重积分.对积分区域Ω处理时需要用区域不等式,而不能使用区域边界方程等式.这时由于有些时候会产生两个区域,如后面例2.但用区域不等式就可以避免这类问题。对Dzr区域进行平面分解时候,可以根据实际情况采取合适的积分次序。
四 球坐标法


注3.通过降维方法,三重积分投影法和截面法本质上就实际上是计算二重积分和定积分,而柱坐标法就变成平面直角坐标系z-r上的二重积分,球坐标法就变成极坐标系r上的二重积分.
注4.实际计算三重积分时,应该还需结合对称性,轮换性等若干性质对积分进行转化.
注5.文中方法均是以z为研究对象,对于其它情形也可用类似方法;有时候也需要对区域进行分割再降维.
例1设Ω是由曲面z=xy,z=0,y=x,x=1围成的空间区域,求xyzdxdydz.分析此题应用投影法,利用z=xy和z=0推出
x=0或y=0,再联立y=x,x=1就可知道投影Dxy可写为:

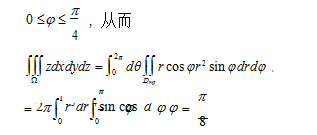 五结束语
五结束语
本文所介绍的三重积分的降维方法,与传统计算方法相比优势明显:避免画出立体积分区域,只需掌握二重积分的直角坐标系法和极坐标法相关知识即可。当然,任何方法并不是万能,都有特定的使用条件。因此,需要根据积分区域,被积函数对称性及其轮换性等各方面因素综合选择最合适的计算方法。
参考文献
[1]同济大学数学系编.高等数学(第七版,上下册)[M].北京:高等教育出版社,2014.
[2]梅加强.数学分析[M].北京:高等教育出版社,2011.
[3]严玉清,张振华.积分的对称性计算方法研究[J].教育现代化,2015(17):70-75.
[4]严兴杰,祁伟.定积分第一中值定理的一点注记[J].教育现代化,2017,4(30):136-138.
[5]廖立胜,陈佳毅.全息投影技术在幼儿教学中的应用[J].教育现代化,2016,3(08):109-111.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/27438.html