SCI论文(www.lunwensci.com):
摘要:本文提出了将MAPLE数学软件引入到材料力学课程结论推到过程的思路,简化了材料力学学习过程中推导结论的复杂过程。分别从材料力学中选取工字钢弯曲切应力推导和平面应力状态中主应力公式推导这两大内容进行编程举例说明。程序运行结果显示了该思路的正确和便利,使应用型本科类院校学生精力从繁琐的数学计算中解放出来以便致力于解决实际问题。
关键词:MAPLE;材料力学;公式推导;应用型本科
本文引用格式:陈辉,等.MAPLE在推导材料力学公式中的应用[J].教育现代化,2019,6(35):133-136.
《材料力学》课程是研究线弹性结构的材料在外部荷载下的强度、刚度和稳定性的一门学科,是机械制造、土木工程、各类材料相关专业重要的专业课程之一,是后续《机械原理》、《结构力学》、《弹性力学》等课程的基石,也是进行结构设计和机械制造或设计的基础,更是解决实际工程问题的重要手段和方法,是一门理论联系实际的重要课程。然而该课程内容繁杂、公式多、推导计算多、理解困难、不容易掌握,导致一定比例的同学上课时思路跟不上,课后作业较难完成,考试不及格率偏高,应用到各专业的课程设计阶段或者是毕业设计阶段的能力也非常欠缺,在实际工程问题中更是无法做到学以致用。因此,在技术应用型地方院校本科人才培养的大背景下,《材料力学》课程的教学改革迫在眉睫[1]。
在《材料力学》课程的教学中,主要存在以下两个问题:一是过于注重理论知识或结论的推导。以弯曲应力这一内容为例,弯曲应力的结论本身表达式非常简单,但其结论的由来则涉及到几何学、物理学、静力学和数学积分的综合应用[2]。对于任何定理,必须知道它的整个由来或者说从概念上完全清楚才能正确熟练的运用。但由于应用型本科院校学生数学基础相对来说有所欠缺,在学习材料力学这门课程中势必会耗费巨大精力甚至都不能完全弄懂。而且在这个过程中大部分学生极易产生消极的学习情绪,这样就会使得学生从理论学习到实际应用都达不到培养目标,难以服务于社会;二是在学生用所学的材料力学知识去解决实际问题时,面对的都不是简单结构或者问题,课本所学知识往往都是靠手算解决,而实际工程问题大多都很难用手算或者根本无法用手算解决。所以即使学生很好的掌握的材料力学的理论知识,但在应用中也是力不从心,无从下手。
文章将结合作者近几年的教学经验,通过引入MAPLE这一强大的符号运算软件来改善上述两个问题。MAPLE是世界上最为通用的数学和工程计算软件之一,其数学和分析功能覆盖几乎所有的数学分支,如微积分、微分方程、特殊函数、线性代数、图像声音处理、统计、动力系统等。而且MAPLE有一些非常好的优点就是可以进行公式的分步推导、各种方程或者方程组的求解,以及对公式进行合并同类项、对函数进行绘图等。同时在材料力学中,绝大多数结论的推导都涉及到该软件涵盖的微积分、线性代数、微分方程求解、动力学、欧拉公式等等。正是由于该软件和《材料力学》的这些特点,将二者结合起来将给《材料力学》等学科教学带来新的启发。文章考虑到材料力学中很大一部分内容涉及到应力计算以及绘制平面应力图。故列举工字钢横截面应力公式和平面应力状态公式结论的推导。
一工字钢横截面应力公式推导
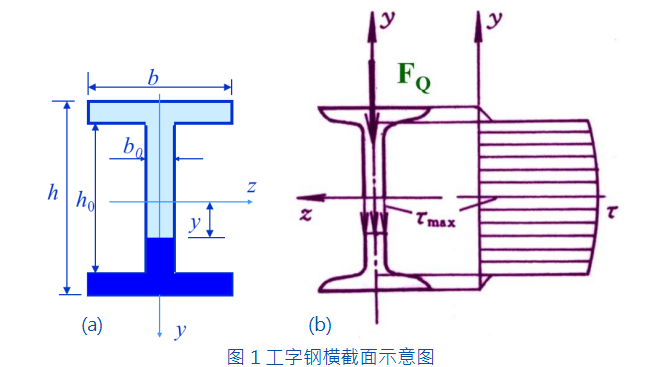
当结构受横力作用发生弯曲变形时,梁横截面上的内力除弯矩以外还有剪力,因而在横截面上除了有正应力还有切应力。在弯曲问题中,一般来说,正应力是强度计算的主要因素,但在某些情况下,如跨度较短而截面较高的梁,其切应力就可能有相当大的数值,这时还有必要进行切应力的强度校核。切应力的分布规律与其横截面的形状有密切关系。在材料力学研究范围内,工字形截面梁是一种主要的梁结构,并且由于其横截面较为复杂,其横截面上的切应力计算推导较为困难。工字钢截面如图1所示,其上下部分的水平放置的矩形为翼缘,中间的细长的竖直矩形为腹板,规定剪力FQ沿y轴方向向下。要求计算整个腹板的弯曲切应力。在距z轴距离为y的腹板等高线上,切应力τ均匀分布,方向与FQ同向,SZ为图1(a)所示阴影部分对z轴的静矩。即在MAPLE中输入:

每一点的正应力都比较大,所以翼缘承担了截面上的大部分弯矩。算例一中,使用 MAPLE 计算横截面静矩的积分, 其中无需进行定积分的繁琐的推导。这大大简化了解题的难度和时间。学生只需要了解基本的定积分知识;在求解工字钢截面静矩后,学生只需要将结果代入应力计算公式中,能非常容易的得到应力计算结果以及应力分布图。整个过程关于力学的部分只有静力平衡方程和应力计算公式,而定积分这一数学问题占据了整个推导过程的大部分工作,进一步观察会发现,结构惯性矩、静矩,极惯性矩等常见的积分问题几乎存在与整个材料力学的各个章节。学生的过多精力耗费在对数学问题的研究上而不是材料力学结论的应用上,会使得学生对材料力学失去兴趣而排斥该课程的学习。对于高等数学基础较差的学生,长期如此更会对材料力学的学习带来极为不利的影响。上述列举的工字钢切应力计算问题提供的求解思路为解决这一问题带来新的启发。
二 平面应力状态公式推导
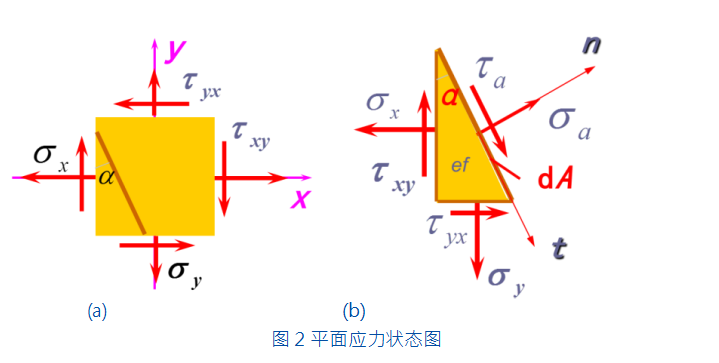
平面应力状态分析,就是在平面应力状态下, 通过一点的某些截面上的应力,计算出这一点的其他方位截面上的应力,从而最终确定该点的主平面、主应力和最大切应力 [2]。从材料内某点截取的微元如图 2 所示。微元前、后两个面上无应力,故前、后两个面为主平面,且这个面上的主应力为零,所以,它是平面应力状态。在图 2(a)所示的微元的各面上,假定应力正交分量 σx、σy、τxy 和 τyx 全部已知。对应力符号定义为: 正应力为拉应力时为正,反之为负;切应力以使微元顺时针旋转时为正,逆时针旋转为负。
现需求解微元任意斜截面ef 上的应力表达式(图2(b))。设该截面外法线 n 与 x 轴的夹角为 α。同时规定:由 x 轴转到外法线 n 为逆时针方向时,则α 取正。取一斜截面 ef 把微元截开,根据力学平衡方程,可以由 MAPLE 解方程组的功能建立平衡方程


算例二中涉及到的学科知识较多,需要用到静力平衡方程、三角函数关系、求导或者求极值以及解方程组等数学和力学知识。不仅如此,涉及到的变量也很多,如果要求学生独立手动推导,则极易使学生对材料力学失去兴趣。从推导结果来看,平面应力状态下的结论相比推导过程而言要简单很多, 从这个角度来看,材料力学本身并不复杂,复杂繁琐之处在于数学推导过程。若整个过程应用 MAPLE 软件进行求解,学生需要掌握的,仅仅是力学里面最基本的受力分析和平衡方程等最基础的力学知识。复杂微积分计算和线性方程组或微分方程求解过程可全部通过MAPLE软件求解。学生对材料力学做到了真正的应用。
以上两个算例涵盖了材料力学中的两种主要问题,具有通用性。通过以上两个问题结合MAPLE软件的推导应用,可以看出,应用MAPLE这一现代工程数学工具来推导材料力学中的结论,可以在很大程度上将学生从繁琐的数学计算中解放出来,使他们可以专注于工程问题的分析推理和建模及实际应用,将数学过程或者环节基本上交给MAPLE软件。能更大的激发学生对材料力学本身的兴趣,从根本上改变了很多学生对力学等理论课程“枯燥”、“乏味”的印象。从而将“应用”这一培养特点很好的体现出来,这种教学模式是一种专注于能力培养的教学模式[6]。
三结语
工科专业的很多专业基础课、专业课中的诸多结论都是由数学尤其是高等数学、线性代数等工程数学计算推导出来。实际工程人员或者工程专业的学生则主要是应用这些重要结论。由于数学较为抽象,且地方院校的工科学生数学基础相对来说较为薄弱。在该类院校的教学过程中,若推导过程不熟悉,则对推导或计算出的结论会不牢固。用该知识解决实际工程问题时更易遇到数学瓶颈。另一方面这些学生推理建模及动手能力和科研型高校大多数学生相比差距不大。因此,有了MAPLE这一强大的符号运算软件作为有力工具,地方院校学生在应用专业知识解决实际工程问题的效率和效果将会大幅提高。其学习能力,实践能力和创新能力将会有很大的改善。另外,结构力学以及弹性力学等推理性较强的力学课程中也有很多理论的推导都较为复杂,如何将MAPLE应用到这些课程中,培养学生在这些理论性较强课程中的专业素养和兴趣,值得进一步研究。
参考文献
[1]闫冰洁.浅谈基于地方本科高校应用型人才培养的材料力学教学改革[J].大学教育,2015(12):144-146.
[2]刘鸿文.材料力学.Ⅰ.第5版[M].北京:高等教育出版社,2011.
[3]管靖,彭芳麟,胡静,等.理论力学教学现代化——“理论力学计算机模拟实验”课程的探索[J].大学物理,2001,20(8):38-40.
[4]李银山.MAPLE理论力学[M].北京:机械工业出版社,2006:1-390.
[5]邢静忠.代数系统Maple在力学教学中的应用探讨[J].力学与实践,2010,32(4):96-100.
[6]陈辉,宋彦朋.MAPLE在应用型本科理论力学课程中的应用[J].教育现代化,2018,5(14):172-174.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/jiaoyulunwen/10142.html