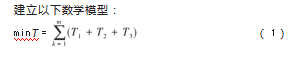摘要:中小型物流企业规模小,长途运输路线单一,卸货及后续送货服务常外包合作方,针对这些基础情况,以物流企业运输上端货物收集流程中的车辆调度为优化目标,在考虑货物装卸和道路交通情况下建立最小化服务总时间的车辆路径优化模型,并设计了一种改进和声算法进行求解带时间窗和载重约束的车辆调度问题。其中算法主要改进了音调微调概率,并将遗传算法中的逆序变异代替音调微调带宽,以提高算法的求解速度和准确度。最后将改进微调带宽和声算法和改进遗传算法的算例进行仿真实验对比,实验结果可以表明所提出的改进和声算法能更有效地得到最优解。
关键词:中小型物流企业,车辆路径优化,和声算法,时间窗和载重约束
0引言
车辆路径优化问题(Vehicle Routing Problem,VRP)也可以被称为车辆调度问题,常规含义上讲是指在一定的约束条件下,为一组车辆规划最优的路径,以实现最小化总行驶距离、时间或最小成本等其他目标。这种问题常常在物流、配送、运输等领域中出现[1],目标是提高效率、降低成本,并确保任务按时完成。
带时间窗和带容量约束的车辆调度问题(Capacitated Vehicle Routing Problem with Time Windows,CVRPTM)[2]是车辆路径优化问题中的一个子问题,它结合了车辆的容量限制和时间窗口约束。CVRPTW可以描述为:需要规划一组车辆的路径,以满足一系列客户的需求,并确保车辆在一定的时间窗口内到达每个客户,同时保持车辆容量在可承受的范围内,最终达成路径最短或成本最小的各种目标。由于CVRPTW的实用性与适用性,引起了众多学者的关注与研究。近几年来,由于元启发式算法的研究与发展,元启发式算法也被许多学者应用于CVRPTW的优化与求解,其中常见的主要包括遗传算法[3]、模拟退火[4]、禁忌搜索[5]、蚁群算法[6]等。Thangiah等[7]采用了遗传算法去求解多车场约束下的车辆路径问题;Ombuki B等[8]也采用遗传算法求解带时间窗的车辆路径问题;杨超等[9]采用了改进的麻雀搜索算法,在构建的低碳路径模型中加入了客户满意度;陈凯等[10]采用了改进灰狼算法,在求解最小车辆总成本的同时平衡每辆车的工作量;王飞[11]采用了改进粒子群算法,采取了惯性权重递减的策略避免算法早熟收敛;蔡雨岑[12]采用了平衡鲸算法引入动态平衡策略优化无人车路径规划;Qixing Liu等[13]采用了2opt和遗传算法的混合算法,加入了影响运输过程中的道路地形坡度变化;黄埔生[14]在用NSGA II解决单配送中心可选时间窗车辆调度问题的基础上,利用聚合优化算法进行分区处理,将多配送中心可选时间窗问题转换为单配送中心可选时间窗车辆调度问题;范厚明等[15]设计自适应遗传-大领域搜索算法研究混合时间窗下多中心混合车队车辆路径优化问题;张延[16]提出PACO和MACO混合蚁群算法分别对放式带软时间窗车辆路径问题和式带软时间窗车辆路径问题进行求解;杨华龙等[17]运用干扰管理思想设计基于禁忌搜索新的调度算法对客户时间窗变动的车辆调度进行研究;ZHANG等[18]提出了一种具有遗传机制的自适应离散杜鹃搜索算法对带时间窗和随机服务时间的车辆的问题进行研究;Zhang等[19]提出一种具有全局优化的混合禁忌搜索算法研究带时间窗的多周期药品配送车辆路径问题。但在常见的诸多算法中,缺乏一种简单易实现、适应性强、全局搜索能力强的算法。
本文对CVRPTW优化求解采用的是和声算法(Har⁃mony Search,HS)。和声算法原理上是模拟了音乐演奏[20]。是一种基于自然启发的启发式算法,其应用范围涵盖了许多领域,尤其是在需要求解连续型优化问题时,和声算法具有实现简单、全局搜索能力强、适应性强、适用范围广等优点。为了避免出现局部搜索最优解的情况,本文从调节算法参数这方面上去进行算法优化。首先对算法中音调概率参数进行动态优化,以保障HM种群信息的丰富性,再结合常规遗传算法中的逆序变异步骤替代原和声算法中的的微调带宽步骤,从而达到增加算法的搜索能力的目的。
1问题描述及数学模型
针对中小型物流企业规模小,长途运输路线单一,卸货及后续送货服务常外包合作方的基础情况,本文的优化方向放在了物流企业运输上端的货物收集这一步骤。针对的中小型物流企业的CVRPTW可以描述为存在一个物流中心,拥有若干载货车辆,存在若干客户点,需要载货车辆将客户点货物运输回物流中心。其中问题模型的主要约束为车辆存在载重约束并且客户点存在时间窗约束。针对中小型企业的规模限制导致的企业车辆载力有限,在物流服务高峰期难以满足客户运载需求。在企业竞争压力巨大的基础情况上中小型企业如没能满足客户需求将直接造成客户流失情况。本文将目标函数设为最短车辆总服务时间对车辆调度问题进行优化求解,得到车辆路径优化,提升企业运载效率,增强企业核心竞争力。由于本文以城市交通运输为背景[21],在车辆路径行驶计算上引入道路交通系数,使模型更贴合现实需求。
为了方便描述问题及模型,本文采用表1所示的符号体系进行说明。
6结束语
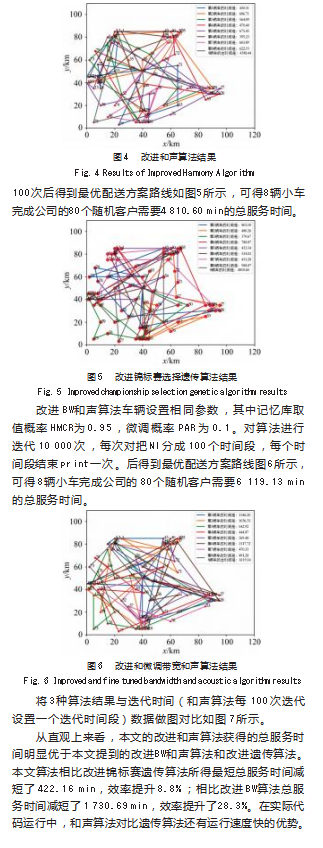
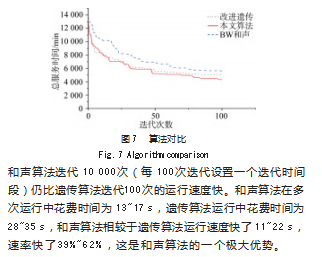
本文将惩罚机制考虑在内,并将企业主要需求运行成本与时间相结合,在这基础上考虑城市实际交通道路系数与工人装卸速度等企业运行实际参数,构建了以最小化总成本时间的为优化目标车辆路径优化模型。根据模型改进了一种和声算法进行求解。对Solomon数据集中的RC108进行分析求解。为了验证算法的有效性与可行性,同时采用改进锦标赛选择遗传算法和改进微调带宽和声搜索算法进行比较。通过实际运行比较可以看出,本文设计的算法在寻优结果都明显优于本文中的另两种算法。但改进和声算法仍保留了和声算法的原有机制,对算法的离散化不够彻底,导致算法的全局搜索效率并不够高,因此今后将根据和声算法和路径规化的性质,设计一种能将数据更加离散的离散和声算法。
参考文献:
[1]Dantzig G B,Ramser J H.The truck dispatching prob-lem[J].Management science,1959,6(1):80-91.
[2]魏明,高成修,胡润洲.一种带时间窗和容量约束的车辆路线问题及其TabuSearch算法[J].运筹与管理,2002(3):49-54.
WEI M,GAO C X,HU R Z.The capacitated vehicle routing prob⁃lem with time windows and its tabu search meta-heuristic[J].Op⁃erations Research and Management Science,2002(3):49-54.
[3]赵振华,王杰,娄春元.基于遗传算法的带时间窗约束车辆路径问题研究[J].物流科技,2007(2):92-95.
ZHAO Z H,WANG J,LOU C Y.Study of the optimizing of distri⁃bution routing problem with time windows based on genetic algo⁃rithm[J].Logistics Sci-Tech,2007(2):92-95.
[4]Yanhui L,Qiong T.Improved Simulated Annealing Algorithm for Location Inventory Routing Problem with Soft Time Windows[C]//Proceedings of the 6th International Conference on Innova⁃tion and Management,2009.
[5]FAN X,LI N,ZHANG B,et al.Research on Vehicle Routing Prob⁃lem with Soft Time Windows based on Tabu Search Algorithm[C]//Proceedings of 2011 IEEE the 18th International Conference on Industrial Engineering and Engineering Management(Volume 1).Institute of Electrical and Electronics Engineers,2011.
[6]李奕颖,秦*.基于Spark的改进蚁群算法对带时间窗车辆路径问题的求解[J].计算机系统应用,2019,28(7):9-16.
LI Y Y,QIN G.Solving vehicle routing problem with time win⁃dow based on spark′s improved ant colony algorithm[J].Comput⁃er Systems&Applications,2019,28(7):9-16.
[7]Thangiah S R,Salhi S.Genetic clustering:an adaptive heuristic for the multi depot vehiclerouting problem[J].Applied Artificial Intelligence,2001,15(4):361-383
[8]Ombuki B,Ross B J,Hanshar F.Multi-objective genetic algo⁃rithms for vehicle routingproblem with time windows[J].Applied Intelligence,2006,24(1):17-30.
[9]杨超,张惠珍,钱陇骏.改进麻雀搜索算法求解多目标低碳冷链物流车辆路径问题[J].包装工程,2024,45(3):251-261.
YANG C,ZHANG H Z,QIAN L J.Improved sparrow search algo⁃rithm to solve the routing problem of multi-objective low-carbon cold chain logistics vehicle[J].Packaging Engineering,2024,45(3):251-261.
[10]陈凯,龚毅光.混合多目标灰狼算法求解多目标VRPTW问题[J].计算机工程与应用,2024,60(11):309-318.
CHEN K,GONG Y G.Hybrid multiple-objective grey wolf algo⁃rithm solving multi-objective vehicle routing problem with time windows[J].Computer Engineering and Applications,2024,60(11):309-318.
[11]王飞.带时间窗车辆调度问题的改进粒子群算法[J].计算机工程与应用,2014,50(6):226-229.
WANG F.Study on vehicle scheduling problem with time win⁃dows based on improved particle swarm optimization[J].Com⁃puter Engineering and Applications,2014,50(6):226-229.
[12]蔡雨岑,杜鹏桢.基于平衡鲸鱼优化算法的无人车路径规划[J].控制与决策,2021,36(11):2647-2655.
CAI Y C,DU P Z.Path planning of unmanned ground vehicle based on balanced whale optimization algorithm[J].Control and Decision,2021,36(11):2647-2655.
[13]LIU Qixing,XU Peng,WU Yuhu.A hybrid genetic algorithm for the electric vehicle routing problem with time windows[J].Con⁃trol Theory and Technology,2022,3(20):279-286.
[14]黄埔生.带可选时间窗的车辆调度多目标优化方法[D].焦作:河南理工大学,2021.
[15]范厚明,杨成,张跃光,等.混合时间窗下多中心混合车队车辆路径优化[J].计算机集成制造系统,2023,29(10):3529-3546.
FAN H M,YANG C,ZHANG Y G,et al.Multi-depot mixed fleet vehicle routing problem with mixed time windows[J].Computer Integrated Manufacturing Systems,2023,29(10):3529-3546.
[16]张延.求解多目标带软时间窗VRP的混合蚁群算法研究[D].淮南:安徽理工大学,2021.
[17]杨华龙,叶迪,张倩,等.时间窗变动的车辆调度干扰管理模型与算法[J].运筹与管理,2017,26(10):56-64.
YANG H L,YE D,ZHANG Q,et al.Disruption management model and algorithm for vehicle scheduling with time window changes[J].Operations Research and Management Science,2017,26(10):56-64.
[18]Zhang G,Wu M,Li W,et al.Self-Adaptive Discrete Cuckoo Search Algorithm for the Service Routing Problem with Time Windows and Stochastic Service Time[J].Chinese Journal of Electronics,2023,32(4):920-931.
[19]Lera Romero G,Bront J J M,Soulignac F J.A branch-cut-and-price algorithm for the time-dependent electric vehicle routing problem with time windows[J].European Journal of Operational Research,2024,312(3):978-995.
[20]Geem W Z.A New Heuristic Optimization Algorithm:Harmony Search[J].Simulation,2001,76(2):60-68.
[21]王立夫,钟昊男,郭戈.基于拥堵系数的道路交通网络关键路段辨识[J].控制与决策,2023,38(3):843-849.
WANG L F,ZHONG H N,GUO G.Identification of key road
sections of road traffic network based on congestion coefficient[J].Control and Decision,2023,38(3):843-849.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/82480.html