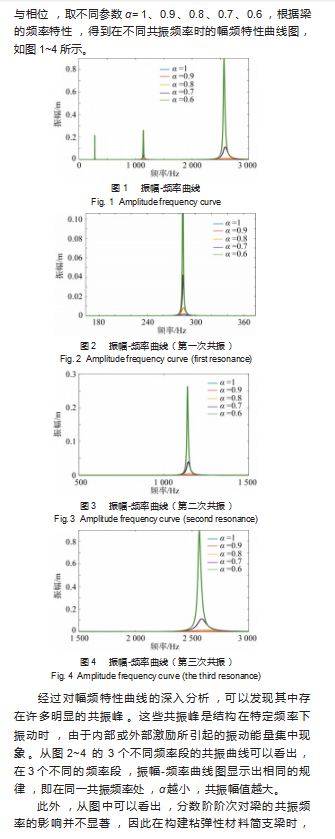
摘要:为了解决整数阶微分方程分析粘弹性梁振动特性的不精确问题,采用分数阶微积分理论对粘弹性材料简支梁进行了详尽的振动分析。基于Euler-Bernoulli梁理论,建立了轴向运动分数阶粘弹性梁的动力学模型,利用伽辽金法求解微分方程并得出相应的解析解,采用Matlab软件对所建数学模型进行数值计算并对不同分数阶系数α(0<α<1)及不同共振频率下的幅频相频曲线图进行分析。研究结果显示,分数阶系数α对梁的共振频率的影响并不显著,α越小,幅值峰值越小,随着阶次α和频率的增加,分数项对相频曲线衰减的影响逐渐增强,分数阶微积分在高频和高阶次的情况下对信号和系统的动态特性具有更强的描述能力。针对粘弹性材料利用分数阶微分方程来构建系统动力学模型,可以使用更少的项数,从而降低微分方程的复杂性,有助于简化模型,减少计算量,同时保留足够的精度。
关键词:分数阶微积分,粘弹性梁,振动分析,Kelvin本构模型
0引言
分数阶微积分诞生于1695年,最早出现于Leibniz给L’Hospital的书信往来中,它与整数阶微积分几乎同时诞生,但直到19世纪末,分数阶微积分的理论体系基本上才被建立并逐渐发展完善起来[1]。20世纪70年代,Bagley[2]在描述粘弹性材料之间的关系中使用到了分数阶导数,并得到了很好的描述效果,进而实现了分数阶微积分的实际应用[3]。Di Paola等[4]采用Caputo定义的双参数分数阶本构模型,对粘弹性材料的蠕变和应力松弛两种现象进行描述。Zhang和Simizu[5]则基于分数阶Kelvin模型,对同类材料的阻尼特性进行研究。Eldred等[6]对比了Kelvin模型、分数阶Kelvin模型、三参数以及四参数分数阶模型,认为分数阶模型更适合于在较大的频率范围描述粘弹性材料的性能。杨俊[7]采用双分数阶本构模型研究橡胶材料的粘弹性特性。段灵杰和段俊生[8]提出了一个含分布阶导数的分数阶粘弹材料本构模型,并将其用以对粘弹性杆-质量块系统的稳态振动分析。近年来,分数阶微积分在自然科学与社会科学的各个领域的研究和应用呈现出欣欣向荣的趋势。分数微积分在各个学科领域都产生了深远影响,包括粘弹性材料的本构关系研究[9]、粘弹性材料的蠕变和应力松弛[10]、量子力学、岩土工程、航天航空[11]、电气工程、生物医学[12]、生物工程、信号和图像处理、机电一体化、控制理论[13-14]、和地震的奇异性分析[15]等。
随着粘弹性材料科学的进步,其在梁结构领域的利用也日益普及。由于粘弹性材料在变形过程中存在不可逆的松弛和蠕变现象[16],粘弹性梁的振动变形是复杂的这一现象也被称为记忆效应[17]。对于粘弹性材料来说,整数阶模型以及分数阶模型均可用于描述材料的力学特性,但由于分数阶算子具有记忆性和非局部性,非常适合用于描述粘弹性材料这种具有记忆性和遗传特性的材料,因此分数阶模型比经典的整数阶模型有着巨大的优越性[18]。经典粘弹性模型需要更多的参数来描述材料的性质,且基于整数阶模型获得的材料特性在宽频范围内无效[19]。分数阶模型能够用少量的参数在宽频范围内描述粘弹性材料的力学性能,其能够反映更真实的粘弹性材料力学特性。为了更好地拟合粘弹性梁的振动特性,本文采用分数阶微分方程来建立梁振动的动力学模型,通过改变分数阶阶数来寻求最接近梁振动的数学模型。
1分数阶微积分的概念
分数阶微积分是应用数学的一个领域,涉及任意阶的导数和积分。分数演算的3个主要定义是Riemann-Lowville(R-L型)、Grunwald-Letnikov(G-L型)和Ca⁃puto的定义,其中R-L型和G-L型适用于初值为零的问题求值,而Caputo适用于初值不为零的问题求解[20]。G-L定义是将经典的整数阶微分的阶数从整数阶推广到分数阶,通过递推公式求极限得出的,在数值实现时可以转换为卷积运算形式,因此非常适合在信号处理中的应用;R-L定义是G-L型微积分的扩充,可以简化分数阶微积分的计算过程,所以主要应用于计算一些较为简单函数的解析解;由于G-L型和R-L具有超强的奇异性,在工程技术领域的应用和物理建模中受到限制,意大利地球物理学家Caputo提出了一种弱奇异性质的定义,即Caputo分数阶导数,它广泛适用于分数阶微分方程初边值问题的分析,在许多实际问题的建模中得到了广泛的应用。3种关于分数阶微积分定义之间存在着紧密的联系,在一定条件下可以相互转换。
1.1分数阶微积分的定义
一般来说,Caputo型分数阶导数由于其便于分析分数阶微分方程的初边值问题,更适用于数学模型的建立,故本文所研究的分数阶粘弹性材料梁的振动模型是建立在Caputo型分数阶导数的基础上的。
4结束语
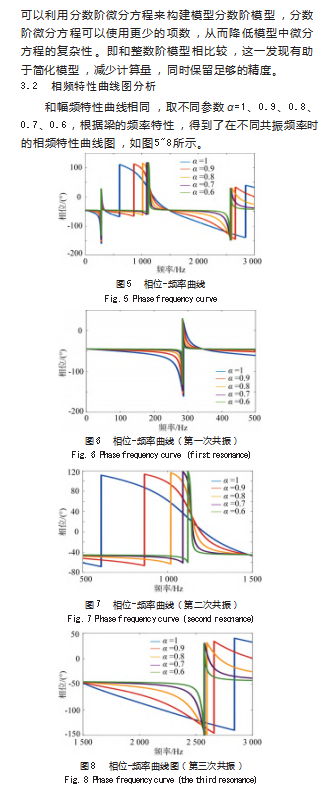
本文采用分数阶微积分理论对粘弹性材料简支梁进行了详尽的振动分析,在传统梁的振动理论中引入分数阶的概念,对简支梁给出了新的数学模型,并用Matlab计算得出粘弹性梁的幅频及相频图,分析得到了如下结论:粘弹性材料是一种特殊的材料,具有同时表现出弹性和粘性特性的能力。在振动过程中,粘弹性材料的阻尼作用可以有效地消耗振动能量,从而降低结构的振幅,减小振动对结构的影响。通过对幅频特性曲线的深入分析,可以更加全面地了解结构的振动特性,掌握结构在不同频率下的响应规律。同时,分数阶的引入提供了一种新的视角和方法来研究结构的动态行为,为结构的设计和优化提供了新的思路。分数阶微积分在相频特性方面展现出了与整数阶不同的特点,如共振频率处的相位跳变和随阶次和频率增加而对相频曲线衰减的影响增强。这些特点使得分数阶微积分在为粘弹性材料的选取、建立更为准确的振动模型以及设计减振结构等方面具有更广泛的应用前景。
参考文献:
[1]吴强,黄建华.分数阶微积分[M].北京:清华大学出版社,2016.
[2]Bagley R L,Torvik P J.Fractional calculus-A different ap⁃proach to the analysis of viscoelastically damped structures[J].AIAA Journal,1983.
[3]胡涤尘.含分数阶和分布阶导数的振动系统分析[D].上海:上海应用技术大学,2022.
[4]Di Paola,A Pirrotta,A Valenza.Visco-elastic behavior through fractional calculus:An easier method for best fitting experimen⁃tal results[J].Mechanics of Materials,2011,43(12):799-806.
[5]Zhang W,Shimizu N.Damping properties of the viscoelastic ma⁃terial described by fractional Kelvin-Voigt model[J].JSME Inter⁃national Journal.Series C,1999.
[6]Eldred L B,Baker W P,Palazotto A N.Kelvin-Voigt vs fraction⁃al derivative model as constitutive relations for viscoelastic mate⁃rials[J].AiaaJournal,2012,33(3):547-550.
[7]杨俊.橡胶弹簧动态特性研究[D].成都:西南交通大学,2015.
[8]段灵杰,段俊生.利用分数阶导数模拟的粘弹材料振动模型[J].应用技术学报,2017,17(4):365-368.
DUAN L J,DUAN J S.Vibration model of viscoelastic materials simulated by using fractional-order derivative[J].Journal of Technology,2017,17(4):365-368.
[9]陈立群,程昌均.分数导数型本构关系描述粘弹性梁的振动分析[J].力学季刊,2001(4):512-516.CHEN L Q,CHENG C J.Vibration analysis of viscoelastic beams with fractional derivative constitute relation[J].Chinese Quarter⁃ly of Mechanics,2001(4):512-516.
[10]徐俊.分数阶粘弹性梁振动特性分析与控制研究[D].南京:南京林业大学,2021.
[11]李冬阳,张张,徐志刚,等.粘弹性材料钻削温度预测模型的建立与应用[J].机械设计与制造,2024(3):166-170.
LI D Y,ZHANG Z,XU Z G,et al.Establishment and application of drilling temperature prediction model for viscoelastic materi⁃als[J].Machinery Design&Manufacture,2024(3):166-170.
[12]汪飞,孙宜楠,张宝媞,等.分数阶微积分模型DWI结合SMS技术在乳腺良恶性病变中的应用价值[J].磁共振成像,2024,15(1):48-54.
WANG F,SUN Y N,ZHANG B T,et al.Differentiation of be⁃nign and malignant breast lesions using DWI with a fractional-order calculus model based on SMS technique[J].Chinese Jour⁃nal of Magnetic Resonance Imaging,2024,15(1):48-54.
[13]王飞,周爱美,王宇霄.一种基于分数阶的非线性积分滑模控制算法[J].机电工程技术,2023,52(3):173-176.
WANG F,ZHOU A M,WANG Y X.A nonlinear integral sliding mode control algorithm based on fractional order[J].Mechanical&Electrical Engineering Technology,2023,52(3):173-176.
[14]周爱美,王飞.分数阶微分D~λ型迭代学习算法在机器人控制中应用[J].机电工程技术,2022,51(5):233-237.
ZHOU A M,WANG F.D~λtype iterative learning algorithm and its application on robot based on fractional calculus[J].Me⁃chanical&Electrical Engineering Technology,2022,51(5):233-237.
[15]葛腾.高耗散粘弹性材料研制及其减震结构分析[D].南京:东南大学,2022.
[16]林中亚.先进材料跨尺度强化、软化及粘弹性的理论和实验研究[D].北京:北京大学,2022.
[17]Jun Xu,Yandong Chen,Yongpeng Tai,et al.Vibration analysis of sandwich beams with viscoelastic coating described by frac⁃tional constitutive equation[J].Mechanics of Advanced Materi⁃als and Structures,2020:1-11.
[18]Mokhtari M,M R Permoon,H Haddadpour.Dynamic analysis of isotropic sandwich cylindrical shell with fractional viscoelastic core using Rayleigh-Ritz method[J].Composite Structures,2018.
[19]Arikoglu A,I Ozkol.Vibration Analysis of Composite Sandwich Plates by the Generalized Differential Quadrature Method[J].AIAA Journal,2012,50(3):620-630.
[20]盛永智,甘佳豪,张成新.弹道可调的落角约束分数阶滑模制导律设计[J].航空学报.2023,44(7):182-195.
SHENG Y Z,GAN J H,ZHANG C X.Fractional order sliding mode guidance law design with trajectory adjustable and termi⁃nal angular constraint[J].Acta Aeronautica et Astronautica Sini⁃ca,2023,44(7):182-195.
[21]杨晓东,陈立群.粘弹性轴向运动梁的非线性动力学行为[J].力学季刊,2005(1):157-162.
YANG X D,CHEN L Q.Nonlinear dynamical behaviors of an axially moving visco-elastic beam[J].Chinese Quarterly of Me⁃chanics,2005(1):157-162.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/82477.html