摘要:组合导航在日常生活中的使用日益增多,其常用的滤波算法为卡尔曼滤波算法,鉴于常规卡尔曼滤波在组合导航系统发生激变时,算法对激变状态跟踪性能不佳的局限性。为了提高组合导航系统对运载体状态发生激变时的追踪能力,提出利用强跟踪算法与无迹卡尔曼滤波算法进行结合,进行互补,形成强跟踪无迹卡尔曼滤波算法。利用无迹变换代替强跟踪滤波中的雅可比矩阵的求解,简化了计算步骤。强跟踪无迹卡尔曼滤波算法既有鲁棒性强、实现简单的优点,也有滤波精度高的优点。通过实验对比EKF、UKF和STUKF分别在组合导航系统中的定位性能。结果表明:EKF在仿真中的定位误差为0.4 m;UKF的定位误差为0.33 m;STUKF的定位误差为0.3 m;STUKF相比EKF和UKF的定位精度有所提升,分别提升了25%和0.09%。验证了该算法的有效性。
关键词:组合导航,渐消因子,强跟踪滤波,无迹卡尔曼滤波
0引言
组合导航系统是一种通过将两个独立导航系统产生的位置信息通过数据融合算法进行融合,以获取比单个系统更高精度的系统输出位置信息的导航技术。常见的组合导航系统主要由卫星导航系统(Global Navigation Satellite System,GNSS)和惯性导航系统(Inertial Navi‐gation System,INS)组成。在实际应用中,组合导航系统的数据融合算法至关重要,而卡尔曼滤波算法是其中的一种常用方法。然而,传统的滤波算法如扩展卡尔曼滤波(Extended Kalman Filter,EKF)存在鲁棒性较差、雅可比矩阵求解复杂等问题。因此,针对这些问题,研究新型的滤波算法以提升组合导航系统的性能成为当前的研究热点。鉴于EKF存在的问题,研究者们不断探索新的滤波算法。英国学者朱里亚等人提出了无迹卡尔曼滤波(Unscented Kalman Filter,UKF),该方法通过近似系统概率分布来实现滤波,无需将非线性函数进行线性化处理,因此在某些情况下估计精度比EKF要高。然而,UKF在计算量较大时会导致滤波精度下降,且在样本值中存在异常值时,滤波精度误差较大。因此,需要寻求一种既能解决EKF的鲁棒性问题,又能避免UKF计算量大和异常值影响的方法。
为了解决上述问题,本文提出将强跟踪算法与无迹卡尔曼滤波算法进行组合,形成强跟踪无迹卡尔曼滤波算法(Strong Tracking UKF,STUKF)。强跟踪滤波(Strong Tracking Filter,STF)是在EKF的基础上改进得到的,能够有效解决运动载体状态突然发生激变时卡尔曼滤波对状态检测效果不明显的问题。通过将STF与UKF相结合,可以充分利用两者的优点,提高组合导航系统的估计精度。
本文预期通过MATLAB进行仿真验证,将STUKF与EKF和UKF进行对比,验证STUKF在组合导航系统中的应用效果。预期结果表明,STUKF能够在保持较高估计精度的同时,解决EKF和UKF存在的问题,为组合导航系统的性能提升提供新的解决方案。
1卡尔曼滤波算法
组合导航系统中,状态方程和观测方程均为非线性方程,最初的卡尔曼滤波算法为线性卡尔曼滤波,对非线性系统的估计结果不准确[11]。因此学者提出了扩展卡尔曼滤波算法,扩展卡尔曼滤波将分线性函数进行近似线性化处理,之后利用线性卡尔曼滤波的步骤,对系统的状态进行估计[21]。
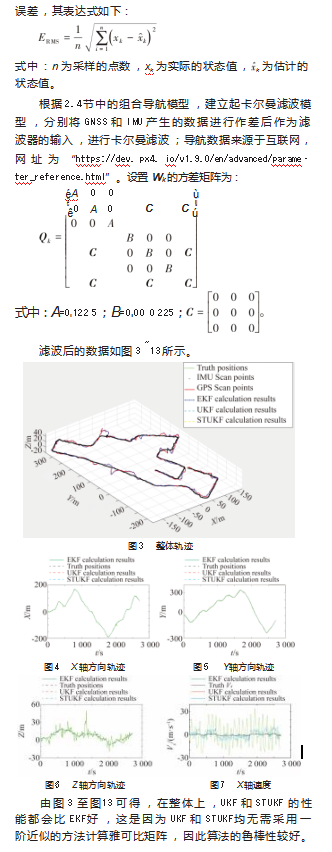
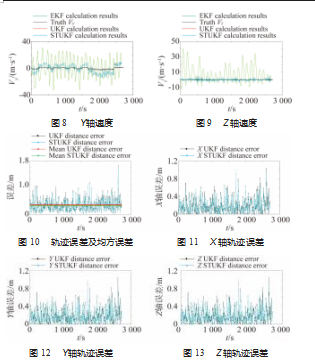
从X,Y,Z三个方向上的轨迹和速度估计可知,STUKF的滤波性能与UKF相差不大,但是从图10~13可知,STUKF在轨迹估计上的曲线比UKF的曲线有一定的收敛,分别计算STUKF和UKF在轨迹上的均方误差,由图10可知,STUKF的均方误差值为0.3 m,而UKF的均方误差值为0.33 m,相较于UKF有了一定的提升,STUKF比UKF提升了0.09%。因此,STUKF在一定程度上优于UKF,应用在组合导航系统中,可以在一定程度上解决载体状态发生激变时滤波性能不佳的问题。
4结束语
本文围绕强跟踪无迹卡尔曼滤波(STUKF)在组合导航中的应用,将传统的组合导航系统的滤波算法替换成STUKF,在相同的情况下,对比EKF、UKF和STUKF在组合导航中的性能,验证了STUKF在组合导航系统中的有效性。同时针对STF中要求解雅可比矩阵才能求解时变渐消因子λk+1的问题,利用UKF中的UT变换的特点,将STF进行等价求解,利用UKF中未引入渐消因子时求解出的输出协方差Pz,k+1及其互协方差Pz,k+1,进而求得STF算法中的渐消因子。通过将渐消因子引入到状态协方差矩阵和输出协方差矩阵中,提高了定位的精度和系统的鲁棒性[12]。通过实验对比EKF、UKF和STUKF分别在组合导航系统中的定位性能,EKF在仿真中的定位误差为0.4 m,UKF的定位误差为0.33 m,STUKF的定位误差为0.3 m,STUKF的定位精度比EKF和UKF分别提升了25%和0.09%;同时在系统发生激变时,STUKF能够对状态进行很好的跟踪,具有一定的平滑功能。
上述的仿真实验均是在卫星定位系统能正常工作的情况下进行的,当卫星失锁导致卫星定位系统不能正常工作时,此时无法为滤波器提供正常的输入,导致滤波器暂时不能正常工作,因此可以引入神经网络来辅助卡尔曼滤波,解决卫星失锁时无法提供定位信息的问题。因此,在今后的工作中,可以引入相应的神经网络,在卫星定位系统正常工作时,对网络进行训练;在卫星信号丢失时通过神经网络来提供丢失的卫星定位信息,使滤波器能够正常工作。
参考文献:
[1]黄小平,王岩.卡尔曼滤波原理及应用:MATLAB仿真[M].北京:电子工业出版社,2015.
[2]王新龙.惯性导航基础[M].西安:西北工业大学出版社,2019.
[3]赵嘉凡.基于CKF算法的SINS/BDS超紧耦合组合导航方法研究[D].呼和浩特:内蒙古大学,2022.
[4]王小旭,赵琳,夏全喜,等.基于Unscented变换的强跟踪滤波器[J].控制与决策,2010,25(7):1063-1068.
[5]牛胜锁,王康乐,梁志瑞.基于改进强跟踪无迹卡尔曼滤波的电力系统同步相量估计方法[J].电网技术,2019,43(9):3218-3225.
[6]周东华,席裕庚,张钟俊.非线性系统带次优渐消因子的扩展卡尔曼滤波[J].控制与决策,1990(5):1-6.
[7]JULIER S,UHLMANN J,DURRANT-WHYTE H F.A new meth‐od for thenonlinear transformation of means and covariances in filters and estimators[J].IEEE Transactions on Automatic Con‐trol,2000,45(3):477-482.
[8]JULIER S J,UHLMANN J K,DURRANT-WHYTE H F.A new approach for filtering nonlinear systems[C]//Proceedings of 1995 American Control Conference-ACC′95,Seattle.WA,USA,1995:1628-1632.
[9]JULIER S J,UHLMANN J K.The Scaled Unscented Transforma‐tion[J].IEEE Transactions on Automatic Control,2002,47:1408-1409P.
[10]吴凤柱.GPS/SINS组合导航系统在自寻的导弹中的应用研究[D].南昌:南昌航空大学,2013.
[11]唐鹏.基于ADS-B数据监视性能评估技术研究[D].天津:中国民航大学,2015.
[12]王康乐.突变环境下电力信号参数估计算法研究[D].保定:华北电力大学,2020.
[13]张红叶,杨毅,修春娣.基于MEMS-IMU的室内定位系统设计与实现[C]//中国高科技产业化研究会智能信息处理产业化分会.北京:第十四届全国信号和智能信息处理与应用学术会议论文集,2021:283-288.
[14]王婷,万志敏,曹健,等.一种基于无迹变换的结构状态/参数/载荷联合识别方法:CN202111054039.8[P].2024-03-07.
[15]王康.基于交互多模型的水下目标跟踪算法[D].宁波:宁波大学,2017.
[16]贺姗,赵旭,师昕.改进的强跟踪求积分卡尔曼滤波算法[J].计算机技术与发展,2018,28(7):43-47.
[17]徐树生,林孝工,赵大威,等.强跟踪SRCKF及其在船舶动力定位中的应用[J].仪器仪表学报,2013,34(6):67-73.
[18]李刚,解瑞春,宗长富,等.基于强跟踪容积卡尔曼滤波的车辆行驶状态估计[J].汽车技术,2015(9):53-58.
[19]刘广哲,张科,吕梅柏,等.基于扩展卡尔曼滤波算法的双模制导仿真研究[J].航空兵器,2018(1):27-32.
[20]罗永平.基于无迹粒子滤波的配电网状态估计研究[D].贵阳:贵州大学,2020.
[21]于佳会,刘佳静,郑建明.多源多维数据融合研究态势:理论、方法与应用[J].情报杂志,2022,41(5):133-138,207.
[22]叶晨,崔双喜.一种强跟踪UKF及其在GPS/SINS深组合导航中的应用[J].导弹与航天运载技术,2018(2):61-64,74.
[23]康伟德.基于SINS/BDS/GPS组合导航信息融合算法研究[D].呼和浩特:内蒙古大学,2019.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/81503.html