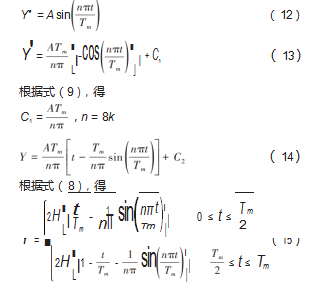摘要:针对四足机器人在运行过程中稳定性较差的问题,设计了一种基于Trot步态的12自由度全肘式四足机器人。首先,建立D-H参数坐标系,选定机身平台为基坐标系,并对目标坐标系下的连杆位置坐标进行运动学解算,选定机动性强且运动范围较广的Trot步态;其次,针对搜救场合对腿部构型的需求,完成了机器人的全肘式腿部结构设计,其中髋关节负责侧摆运动,膝关节和踝关节负责俯仰运动;然后,基于Trot步态进行机器人足端轨迹规划,并导入ADAMS软件进行运动仿真分析,给各部件配置合适的参数后,加入各关节的驱动函数。经仿真分析,机器人在多种运动状态下运行平稳,关节输出曲线平滑,站立蹲起时膝关节最大角速度为45(°)/s,前进时整体路线偏移在2.4%以内,足端路线偏移在3.2%以内。最后设计了机器人实物,通过测试机器人的站立、蹲起和前进等动作,验证了所设计四足机器人的稳定性和机动性。
关键词:四足搜救机器人,D-H参数,Trot步态,足端轨迹,ADAMS
0引言
近年来自然灾害频发,灾害发生后在短时间内开展搜救活动可以大幅提高受灾者的获救概率。但灾后的环境往往比较复杂,不利于救援工作的开展,而且传统的人工救援存在效率低、成本高、危险性大等不足[1]。四足机器人由于其较好的地形适应性和机动性,成为了搜救机器人的首选,因此,四足搜救机器人的研发异常迫切[2]。
1995年1月发生在日本的大地震造成人员死亡超过6万人,随后4月在美国Oklahoma的联邦大楼发生的恐怖主义事故,使得世界各国对搜救机器人的开发更加重视[3]。搜救机器人在城市环境中首次开展救援任务是在美国9.11事件中[4]。之后美国TATRC和TARDEC联合研发了一款多任务、基于系统协作的子母式搜救机器人系统,其具有遥控、半自主和自主控制能力,可近距离抢运伤员[5]。卡内基-梅隆大学研制了超冗余度蛇形救援机器人,机器人的每个模块中都包括电机驱动、齿轮减速以及线驱动制动器,同时配备有多种传感器[6]。
在国内,由中国地震应急搜救中心和中科院沈阳自动化研究所共同研制的“废墟搜索与辅助救援机器人”[7],采用履带式设计,可以替代救援人员进入危险地区进行搜寻和定位。江苏八达重工的BDJY38SLL地震抢险救灾机器人曾在四川雅安地震救援中用来清理废墟和拆除受损房屋,发挥了重要作用[8]。云深处科技与某消防总队联合推出的四足机器人绝影X20,可以加装多种功能模块,进一步拓展了机器狗的应用场景[9]。
目前搜救机器人主要分为轮式、履带式和足式。轮式机器人的结构相对简单,运行响应及速度较快,但其环境适应能力较差,通常只能用在平坦场地。足式机器人的行走机构灵活性强,可应用于复杂场地和崎岖路面,但由于其结构复杂,维持平衡的难度较大。履带式机器人越障能力强,适应地形能力较好[10-11],但体积大、功耗高、灵活性低,无法进入较小的废墟中进行搜救[12]。
在灾后救援场景中,机器人需能完成穿越废墟、自主搬运障碍物、传输信息等工作[13],但四足机器人结构复杂,存在运动过程中稳定性较差的问题。针对该问题,本文设计了一种12自由度的四足机器人,基于Trot步态对腿部结构进行设计,并对足端轨迹进行了优化。仿真分析和实物验证均证明了该机器人的稳定性和机动性。
1机器人运动控制设计
1.1结构设计
为使机器人具有较好的稳定性,通常采用比较低的重心,因此髋关节需位于机器人身体的两侧。
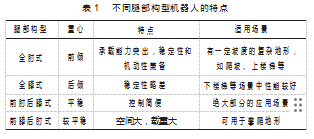
为更接近于仿生学,四足机器人的双前腿均采用相同构型,双后腿也采用相同构型,这也更利于步态规划和电机控制。四足机器人的腿型包括全肘式、全膝式、前肘后膝式和前膝后肘式4种结构,其特点如表1所示。
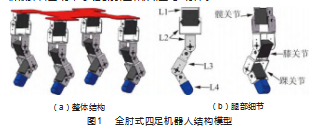
针对救灾需求,基于以上腿部构型的特点,综合考虑四足机器人运动过程中的稳定性和机动性,本文设计了一种12自由度的全肘式机器人。机器人的每条腿有3个自由度,分别位于为髋关节、膝关节和踝关节,如图1(a)所示。
根据模型构造的原则,同时考虑到各零部件间的高连接气密性要求,综合完成结构设计。整机模型的长宽高分别为300 mm、250 mm和223 mm,以基座为关节编号0开始命名各连杆,符号分别为L1、L2、L3、L4,尺寸分别为37.1 mm、63.0 mm、68.6 mm和70.2 mm,同时将前后腿之间的距离设定为250.0 mm,左右腿之间的距离设定为200.0 mm。
腿部关节的三维模型如图1(b)所示,其中髋关节做侧摆运动,负责转向和爬坡等动作。膝关节和踝关节做俯仰运动,负责前进和后退等动作。
1.2正运动学分析
本文采用D-H参数法进行正运动学分析。机器人的每个连杆都可以用连杆长度αi、连杆偏距di和关节角θi这3个运动学参数来表示,用来描述连杆本身及连杆之间的连接关系[14]。
1.3步态及轨迹规划
完成正运动学解算后,即可对腿部各关节的摆动进行设计。足式机器人在运动过程中,腿部摆动顺序不同,对应的时序也会不同,从而形成了不同的运动步态,产生了不同的运动方式。根据四足动物的平衡特性,四足机器人的步态可划分为Walk步态和Trot步态[15]。
1.3.1 Walk步态
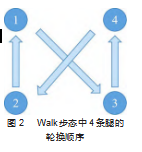
Walk步态是一种静态步态,即在运动过程中始终有3条腿处于支撑相,至多只有一条腿处于摆动相。在Walk步态中,4条腿最常见的轮换顺序为1→3→4→2→1,如图2所示。
1.3.2 Trot步态
Trot步态是一种动态步态,适用于中低速跑动,且支持比较大的运动速度范围。中等速度下的Trot步态具有很高的能量效率,在执行紧急任务时,Trot步态能够在快速前进的情况下保持较高的稳定性,这些优势与搜救机器人的运动需求高度契合,因此本文选取Trot步态。
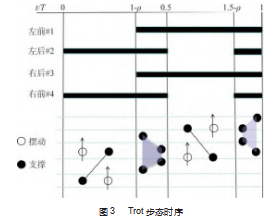
Trot步态的特征是互为对角的两条腿成对运动,即腿1和腿3运动一致,腿2和腿4运动一致,理想情况下对角腿同时抬起并同时着地[16-17]。Trot步态的时序如图3所示,在一个运动周期内,4条腿的抬起时刻分别为t 1=0、t2=0.5和t3=1-ρ,t4=1.5-ρ为处于摆动相的时间。
1.3.3足端轨迹规划
根据Trot步态情况下腿部摆动的特点以及足端摆动轨迹函数为三角函数的复合形式[18],则初步设定曲线方程如式(4)所示。
式中:S为步长;Tm为摆动相周期,且需保证摆动相周期等于支撑相周期。
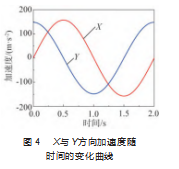
通过对上述公式进行曲线拟合可以得到X与Y方向加速度随时间的变化情况,如图4所示。由图可知,当t=0时,Y方向上的足端产生了较大的角速度,这与理论相矛盾。
此时需要对X方向摆线方程进行优化。摆动曲线类似于正弦函数,不妨设:
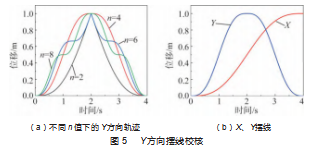
由于H、S、Tm为定值,则需要对n的取值进行校核,如图5所示。由图5(a)可知,当n=4时,曲线拟合较为平滑,故确定n取值4,进而可以确定X与Y方向上的足端摆线函数。足端轨迹如图5(b)所示。
2仿真
根据机器人腿部结构的运动学分析结果,首先在SolidWorks中对四足机器人的结构进行设计,生成三维模型,再将模型文件导入ADAMS进行仿真。由于本文目前主要研究机器人Trot步态的直线行走状态,故只考虑髋关节与膝关节的运动。
首先设置仿真环境,建立机器人的运动跑道,并给各部件设置相应的材料属性。随后在各关节之间的连接处添加旋转副,在机身与腿部连接处添加固定副。最后设定重力方向及大小,在足端设定与地面的接触附着力,确保机器人在跑道上运动,不会因为重力坠落或穿透跑道。根据模型特点,在髋关节与膝关节处设定相应的驱动函数,本文用特定的参数加上正弦函数的形式构成驱动函数,以代替电机驱动,同时设定好相应步长与时间,开展运动学仿真。
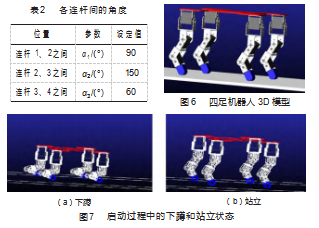
基于运动学分析数据,建立合适的3D模型,初始关节角度数据如表2所示。建立的模型如图6所示。本方案设定,四足机器人在运行前需要先完成从站立到下蹲再到站立的启动过程,如图7所示。
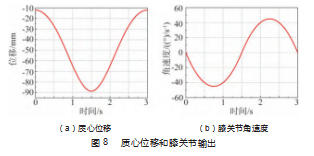
以机身为质心基准,仿真得到机器人质心在此过程中的位移以及膝关节的角速度,如图8所示。从图8(a)可以看出,在此过程中,质心位移曲线平滑,表明机身的稳定性较好,最大蹲起位移为76.6 mm,符合模型的结构要求。从图8(b)可以看出,膝关节角速度较为稳定,输出最高可达45(°)/s,能够为机器人运行提供有力的输出,同样可以证明机器人腿部结构设计的合理性。
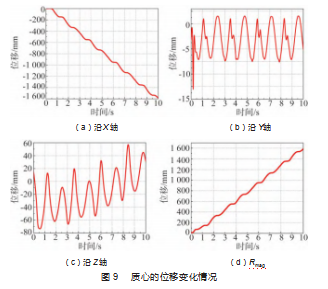
为关节设定合适的驱动函数之后,机器人即可开始运动。四足机器人在前行过程中,可以仿真得到质心位移变化情况,如图9所示。设机器人在XZ平面运动,并沿X负半轴前进。由图9(b)可知,在前进的过程中,质心轨迹沿Y轴的位移曲线较为平滑,在基准线的上下进行摆动,表明关节间支撑、摆动、转动等动作稳定性较好。从图9(a)和图9(c)可看出,机器人在X、Z轴方向上的摆动虽然较为平稳,但随着时间增加却逐渐发生了偏移。这表明,机器人在运行过程中并没有严格沿直线前进,在沿X轴方向前行1 584.61 mm的过程中,Y轴方向最大偏移量为13.10 mm,Z轴方向最大偏移量为58.13 mm,整体路线偏移在2.4%以内。这是由于在本次仿真过程中,机器人在运动时,没有采用实时的校准系统进行反馈控制。从图9(d)中Rmag(各方向位移矢量合成后的模)变化曲线来看,机身整体的稳定性较好。
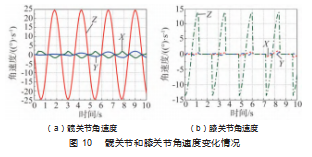
在运动过程中,机器人髋关节和膝关节的角速度变化情况如图10所示。由图可知,机器人在运动过程中,髋关节和膝关节的角速度变化曲线平滑,符合实际情况,其中髋关节沿X、Y和Z轴的最大角速度输出分别为1.87、1.95、24.58(°)/s,膝关节的最大角速度输出分别为1.04、0.76、13.68(°)/s,表明关节提供了稳定而有力的输出,这才使得机身能够整体稳定并维持高机动性。
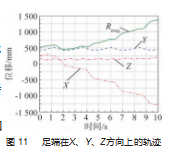
仿真得到的机器人足端轨迹如图11所示,其中Rmag为各方向位移矢量合成后的模。由图9和图11可知,机器人沿X轴方向的位移为1 583.43 mm,沿Y轴和Z轴方向的最大偏移量分别9.45 mm和70.24 mm,足端路线偏移在3.2%以内。足端和质心在各方向上的位移变化趋势几乎相同,在运行中没有发生关节变形或输出量的跳变。仿真结果表明机身整体结构的稳定性较好,同时也证明了模型结构设计的合理性和驱动函数设定的准确性。
3实物设计与验证
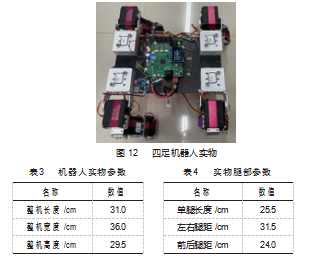
根据运动学设计和仿真分析结果,设计了一款全肘式四足机器人,如图12所示。所设计的机器人实物参数如表3~4所示。
3.1硬件设计
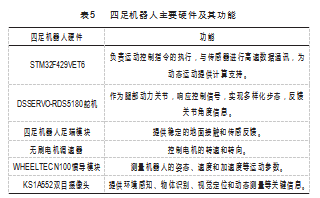
机器人的控制系统核心采用STM32微控制器,控制算法在RT-Thread实时操作系统上开发,其主要硬件及功能特性如表5所示。
舵机选用DSSERVO-RDS5180大扭矩舵机,其扭矩最大为85 kg·m,通过调节PWM波形来对转动角度进行控制。其最大转动角度为270°,适合用于四足搜救机器人。
3.2整机实验
由于在机器人实物中尚未添加实时反馈装置,因此暂无法得到运行过程中腿部各关节的具体数据。但在行走过程中,机身总体保持稳定,未出现明显的倾斜。各关节力矩输出平缓,没有出现因卡顿而导致的关节转动停滞。机器人前进过程中的运动路线和设定路线大致相同。
4结束语
针对四足机器人运行稳定性较差的问题,本文提出了一种12自由度的全肘式机器人,在进行理论分析后建立了3D模型,然后在ADAMS中设定驱动函数,经过仿真和实物测试,证明了本方案的有效性和可靠性,在运行稳定的前提下,关节最大角速度为45(°)/s,为机器人运动提供了强有力的输出。
由于仿真条件受限,机器人在行走过程中会发生路线偏移的情况,前进时整体路线偏移在2.4%以内,足端路线偏移在3.2%以内。在接下来的实验中,会加入实时校准系统,使机器人能够按照规定的路线前行。同时对机器人的各关节进行受力分析,还原真实场景下机器人的运动情况。在机器人实物中添加实时反馈系统,以便于观测运行过程中机器人腿部各关节的变化情况和运动轨迹。以此设计出能够真正投入实际应用的机器人,为救灾作贡献。
参考文献:
[1]杨贵志,高海燕,林智勇,等.煤矿搜救蛇形机器人MK-01控制系统设计[J].煤矿机械,2020,41(5):19-20.
[2]张英杰,面向灾后环境的搜救机器人研制及地图构建技术研究[D].哈尔滨:哈尔滨工业大学,2022.
[3]李磊,叶涛,谭民,等.移动机器人技术研究现状与未来[J].机器人,2012(5):475-480.
[4]于振中,蔡楷倜,刘伟,等.救援机器人技术综述[J].江南大学学报(自然科学版),2015,14(4):498-504.
[5]赵润州,侍才洪,陈炜,等.美军战场救援机器人系统研究进展[J].军事医学,2013,37(4):318-320.
[6]Wright C,Buchan A,Brown B,et al.Design and architecture ofthe unified modular snake robot[C]//International Conference on Robotics and Automation.2016.
[7]Julian Whitman,Nico Zevallos,Matt Travers,et al.Snake Robot Urban Search After the 2017 Mexico City Earthquake[J].2018 IEEE International Symposium on Safety,Security,and Rescue Robotics(SSRR).IEEE,2018:1-6.
[8]饶超.人机协同搜救的任务规划与操控技术研究[D].武汉:华中科技大学,2022.
[9]编辑部.云深处绝影X20极限作业负载刷新记录[J].机器人技术与应用,2022(2):4.
[10]唐梦旖,王倪珂,田畅,等.履带式越障救援机器人的研究及发展综述[J].高校实验室科学技术,2019(2):138-140.
[11]宗成国,王海艳,于晓.履带式煤矿搜救机器人机构设计及越障性能分析[J].煤炭工程,2019,51(10):123-126.
[12]刘健,王增增,李帅,等.基于触觉传感的蛇形搜救机器人的设计与开发[J].机电工程技术,2023,52(11):113-116.
[13]卢孔宝,陈华勇.灾后救援机器人的机械结构设计[J].浙江水利水电学院学报,2018,30(2):54-58.
[14]孔祥瑞.四足机器人轨迹规划与运动学仿真分析[D].北京:华北水利水电大学,2018.
[15]田健.基于欠驱动构型描述的四足机器人自适应步态规划与控制[D].哈尔滨:哈尔滨工业大学,2021.
[16]徐坤,丁希仑,李可佳.圆周对称分布六腿机器人三种典型行走步态步长及稳定性分析[J].机器人,2012,34(2):231-241.
[17]高晗,吴鑫辉,蔡常荣,等.基于慧鱼技术的四足仿生机器人设计[J].机电工程技术,2023,52(8):114-117.
[18]宋凯.一种基于快速控制原型的四足机器人步态设计与运动控制[D].上海:东华大学,2023.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/80673.html