摘要:对轨道自主式螺栓机用螺栓扳手进行结构设计和有限元分析。首先通过计算对螺栓扳手的传动系统做出设计和计算,确定了轨道螺栓扳手的传动方式为二级行星齿轮传动;其次利用SolidWorks软件建立了螺栓扳手齿轮传动和扳手套筒头三维模型,基于建立的模型在SolidWorks Simulation插件中对螺栓扳手套筒头展开有限元计算仿真,分别求解了拧紧螺栓和旋松螺栓两种工况下的静应力和螺栓扳手套筒头的疲劳情况;最后对螺栓扳手套筒头进行动力学模态分析,研究了扳手套筒头和设备内部激励源的共振情况。通过有限元静应力分析,验证了结构设计的合理性,所设计螺栓扳手满足材料强度要求;通过对自主式螺栓机内部激励源频率的计算,对比有限元模态分析得到的螺栓扳手套筒头前6阶固有频率,验证得到所设计结构的动态性能也满足设计要求。
关键词:虚拟样机,轨道螺栓扳手,应力分析,疲劳分析,模态分析
0引言
轨道交通在现代社会中起着至关重要的作用,为城市居民提供了高效的交通方式。然而,确保轨道系统的安全和可靠性是一个复杂的挑战,其中螺栓连接在维护和维修中扮演了关键的角色。轨道螺栓连接不仅支撑轨道的结构完整性,还影响列车运行的安全性和舒适性[1]。在这一背景下,本论文将探讨轨道螺栓扳手的设计、性能和应用,旨在提高轨道交通系统的维护效率和可靠性。
轨道螺栓连接是轨道系统的基本组成部分,它们将不同部件连接在一起,保证轨道的稳定性[2]。这些连接受到日常磨损、气候条件和列车运行的振动等因素的影响,因此需要定期维护和检查。由于传统的螺栓拧紧工具在效率和准确性方面存在不足和缺陷,因此对轨道螺栓扳手的改进和优化是当前轨道维护领域亟待解决的一个大问题。
本论文的目标是深入研究轨道螺栓扳手的设计原理、性能特点以及在轨道维护中的应用。考察现有的螺栓扳手技术,并探讨如何通过改进设计和使用新材料来提高其性能[2],对轨道螺栓扳手进行计算、设计及仿真。利用CAD和CAE理论,设计一款全新的轨道螺栓扳手。
通过深入研究轨道螺栓扳手的相关问题,可以为轨道交通系统的可维护性和可靠性研究作出贡献。这不仅将有助于确保乘客的安全,还将减少维护成本,降低交通系统的停工时间。
1螺栓扳手结构设计
1.1设计原理
轨道螺栓扳手是一种特殊设计的用于紧固或松开轨道系统中螺栓的工具,由扳手套筒头及传动系统组成。扳手套筒头是扭矩输出部件[3],直接接触铁轨上的六角螺栓头。套筒头为六角形,以适应螺栓头的六边形形状,要求套筒头能牢固地包住螺栓头,从而传递扭矩并完成紧固或松开操作。传动系统负责将电机的低扭矩转化成高扭矩输出给扳手套筒头,本文将对轨道螺栓扳手传动系统和扳手套筒头展开设计及仿真。
六角头套筒的尺寸和规格通常根据不同类型和尺寸的轨道螺栓的要求而制造。本文结合中国铁路常用的M36六角头螺栓设计一种螺栓扳手拟应用于轻量化的新一代轨道螺栓作业机。
1.2传动系统
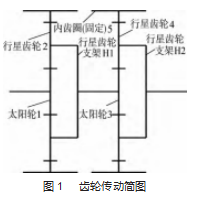
目前行星齿轮传动广泛应用于机械设备中[4],因其具有结构紧凑和工作效率高等优点,尤其在小型设备中具有很强的适配性[5]。在螺栓扳手的应用上可将电机输入的高转速低扭矩通过行星减速器转换成低转速高扭矩的输出结果。本文设计螺栓扳手的减速器基于行星齿轮传动的减速原理[5],由于轨道螺栓的松紧作业属于高负荷大扭矩的作业工况,故本文设计的传动系统为二级行星齿轮传动。传动简图如图1所示,固定太阳轮1与输入电机连接,内齿圈固定,太阳轮带动行星齿轮转动,行星齿轮固定在星架上,星架H1为第一级减速传动的输出轴,也是二级减速传动的输入轴,H1与二级减速传动的太阳轮3连接,同上一级传动相同,太阳轮带动行星齿轮,行星齿轮固定在星架上,星架与负载连接,将电机的低扭矩转变为高扭矩输出给负载[6]。
为了实现功率分流且保证各齿轮间的载荷均匀分布,本文设计的二级行星减速器,高速级传动取行星轮数n=3;低速级传动取行星轮数n=4。
前文设计了传动方案,下文将对各级齿轮进行设计,进而确定本文设计的齿轮传动系统的传动比。
行星齿轮传动系统的约束条件由传动比条件、同心条件、装配条件和邻接条件[7]。
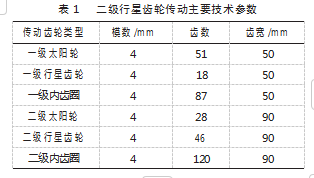
通过计算得到二级行星传动系统的主要技术参数如表1所示。
1.3主体建模
本文扳手套筒头依据铁路常用的M36六角头螺栓设计,套筒头的深度和长度应能够完全包住螺栓头,以确保螺栓头不会滑动或损坏。长度与套筒头的杠杆作用有关,以提供所需的扭矩。由于套筒头经常与金属螺栓头接触,因此本文拟设计的扳手套筒头由高强度合金钢制成,以确保耐腐蚀性和长寿命。轨道螺栓扳手具有一种连接机制,即采用万向节连接方式,以连接件轴的形式设计。这个连接件轴向下通过套筒销连接扳手套筒头、向上通过花键轴连接动力输出系统,使扳手套筒头在左右、上下有一定的活动范围。这种连接通常是可拆卸的,可以在不同的作业环境更换不同尺寸或类型的套筒头。
根据以上设计要求,基于Solidworks对螺栓扳手进行结构设计,如图2所示。
基于前文计算分析得到的传动系统参数,利用Solid‐works建立二级行星齿轮减速器的实体模型,如图3所示。轨道螺栓扳手的装配体如图4所示。
2螺栓扳手静力学分析
2.1有限元法
有限元法(Finite Element Method,FEM)是一种数值分析方法[11-12],用于解决工程和科学领域中的复杂物理问题。它的主要思想是将一个复杂的区域分割成许多小的子区域,称为有限元,然后在每个子区域内建立数学模型,最终将它们组合在一起以获得整个问题的数值解。在求解一个工程问题时,通常将一个或多个区域划分成有限个单元,这些单元相互连接形成网格,再通过定义边界条件,施加载荷进行求解运算,将结果进行可视化处理直观地对工程问题做出结构、热传导、流体力学、电磁学等分析。
2.2 SolidWorks Simulation有限元
SolidWorks Simulation使用有限元分析技术,将复杂的实体模型分解成小的有限元,然后在每个元素上执行数值分析,以模拟物理行为,如应力、位移、温度分布等[13]。SolidWorks Simulation完全基于SolidWorks实体建模。可以直接使用SolidWorks模型,无需导出或转换,与其他主流有限元分析软件相比加快了分析的工作流程。SolidWorks Simulation包括多种分析类型,常见的有静力学分析,以评估物体的静态力学性能;动力学分析,以模拟物体在时间内的动态响应;疲劳分析,以评估零件在多次载荷下的寿命[14]。本文基于该软件对前文设计的螺栓扳手进行静力学和动力学分析。
2.3静应力分析
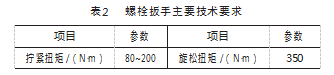
螺栓扳手套筒头是螺栓扳手装置的扭矩直接输出部件,主要用于对螺栓进行拧紧或旋松作业,在工作时所承受的力矩较大,其结构的静态特性直接影响到螺栓扳手装置能否按规定扭矩进行螺栓拧紧或旋松作业。参考《轨枕螺栓机动扳手通用技术条件》[15],轨道螺栓扳手主要技术要求如表2所示。
在扳手材料的选择方面,由于合金钢具有很好的热硬性以及其他特殊性能,如耐热,耐蚀,抗磨以及磁性等,所以在本文的设计中,材料选择合金钢。合金钢的相关属性如表3所示。
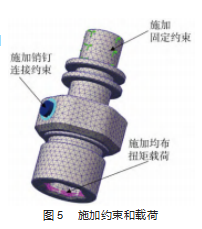
在SolidWorks软件中,对前文设计的结构进行前处理,定义材料、施加约束和载荷和划分网格。分别在扳手头通过花键轴连接减速器位置施加固定约束,在套筒销钉部位施加销钉连接约束,在扳手套筒头内侧施加均布扭矩载荷200 N·m和350 N·m。施加约束和载荷的位置如图5所示。
完成前处理后,分别对拧紧和旋松两个工况进行求解计算,运算结果如图6~8所示。图6为施加200 N·m均布扭矩载荷时的拧紧工况计算结果;图7为施加 350 N·m均布扭矩载荷时的旋松工况计算结果;图8为旋松工况下疲劳分析结果,通过疲劳分析预测螺栓扳手结构的使用寿命。
由图6可知,螺栓扳手在拧紧作业时,承受的最大应力为52.93 MPa,该值远小于材料的屈服极限620 MPa;最大应变为1.928×10-4,局部结构相对变形量微乎其微;已知安全系数=屈服点应力/设计或工作应力[16],在机械设计中,大型重载钢结构的安全系数一般建议取4.5,在本设计仿真中,拧紧作业时,螺栓扳手的最小安全系数为11.7,大于安全系数建议值。从拧紧工况看,本文设计的螺栓扳手满足实际工作要求。
由图7可以看出,螺栓扳手在旋松作业时,承受的最大应力为92.48 MPa,该值小于材料的屈服极限620 MPa;最大应变为3.758×10-4,局部结构相对变形量依然很小,小到可以忽略不计;该工况下最小安全系数为6.7,大于安全系数建议值4.5。从旋松工况看,本文设计的螺栓扳手满足工作实际要求。
在旋松工况的仿真中,引入了疲劳分析。已知旋松工况下,套筒头部位施加的均布扭矩载荷大于拧紧工况,故疲劳分析只用预测旋松工况下螺栓扳手的生命总数值即可。如图8所示,旋松工况下,螺栓扳手的受力部位套筒头结构的最小生命总数约为10万次,即当螺栓扳手在350 N·m的扭矩载荷下,最少工作10万次,结构就会出现不同程度的疲劳损伤,主要受力部位,最小损伤比为21%,说明当螺栓扳手的使用周期达到10万次后,在工程实践中,需要更换螺栓扳手套筒头,不然工作精度和效率会受到影响。
3螺栓扳手动力学分析
为了验证螺栓扳手在轨道螺栓维护过程中能否满足性能要求,需要对螺栓扳手的动态特性进行研究。对结构进行模态分析,验证其是否会与螺栓机内部激励源发生共振[17],以避免可能出现的事故。
3.1模态分析理论
每种结构都有自己的振动频率属性[18],这是一种不依赖于外部负载的固有属性,其运动方程表达式如下:
3.2螺栓扳手模态分析
在真实振动中低阶模态振动占据主导地位,高阶模态在振动过程中转瞬即逝,因此暂不考虑[19]。通过剖析模态分析的运行原理可以知道所要测试结构的振动特性只与其本身的刚度和质量有关,并不受外界载荷影响,因此在进行模态分析时不需要施加载荷与约束条件[20],直接在前文静力学分析的基础上对螺栓扳手前6阶模态进行分析,振型云图如图9所示,前6阶模态固有频率如表4所示。
从图9可以看出,前6阶模态中,螺栓扳手的振型主要是扭转,振动频率分布在2~4 705 Hz,这与无阻尼振动的随机特性相符合。1阶模态中因振动产生的变形主要发生在销钉连接的万向节套筒处,其变化形态对螺栓扳手的实际工作情况影响不大;2~6阶模态中,结构形态变化的位置主要为螺栓扳手工作时与螺栓直接接触的位置,2~6阶模态分析中得出的固有频率在结构设计选型中具有一定的参考意义。故在设备工作过程中内部激励源应尽量避免频率处于1 109~4 705 Hz。
3.3激励源分析
本文设计的螺栓扳手结构应用于轨道自主式螺栓作业机,内部激励源主要是为螺栓扳手提供扭矩输出的直流电机模块[21]。就当前螺栓机设备使用的电机XQ-4分析,电机转速为2 000 r/min,激励频率计算公式如下:
式中:f为电机激励频率;n为电机转速;ε为误差系数,取10 r/min。
通过激励频率计算公式得出,螺栓机设备内部激励源频率为33.5 Hz,对比模态分析结果,激励源频率与各阶次固有频率相差甚远,因此,内部动力源的激励不会导致二者出现共振现象。通过动力学分析,本文设计的螺栓扳手结构完全满足轨道螺栓维护的动力学特性要求。
4结束语
本文通过SolidWorks对螺栓扳手进行了三维建模,通过SolidWorks Simulation对螺栓扳手进行了有限元分析,通过计算求解得到,施加均布扭矩载荷200 N·m和350 N·m两种工况下的应力分布云图和变形云图,考核了结构的应力集中情况。同时得到结构的安全系数等指标,验证了所设计结构的强度合理性。根据模态分析结构,对比自主式螺栓机内部激励源的频率,验证本文所设计结构满足设备工作时的动态性能要求。同时模态分析可作为后续频谱响应分析、频谱分析等其他动力学分析的基础,为螺栓扳手结构的优化设计提供理论依据。
综上所述,本文基于SolidWorks虚拟样机对轨道自主式螺栓机用螺栓扳手进行结构和有限元一体化结构设计及分析,可以为实际生产实践提供可靠的理论参考依据,以达到缩短研发周期,降低研发费用的目的。
参考文献:
[1]王前选,王锐锋,李虎,等.轨道车辆螺栓松动量与预紧力视觉检测方法研究[J].铁道科学与工程学报,2023,20(9):3511-3524.
[2]Failure analysis of anchor bolt of rail fastening system for direct fixation track.Choi Jungyoul;;Kim Byungmin.Engineering Fail‐ure Analysis,2020.
[3]朱毅然.无砟轨道轨距精调车的设计与优化研究[D].上海:上海工程技术大学,2023.
[4]闫政,杨保健,曹云龙,等.自走式山药采收机及其关键部件研究[J].机电工程技术,2023,52(9):31-35.
[5]饶振纲.行星齿轮传动设计[M].北京:化学工业出版社,2014.
[6]吕晓丹,董长双.二级直齿轮行星减速器优化设计研究[J].机械管理开发,2010,25(4):14-16.
[7]赵亚如.混合动力重卡轮毂电机行星减速器设计与分析[D].烟台:烟台大学,2023.
[8]王玉勃.周转轮系传动比计算的通用数值方法[J].机械传动,2016,40(8):181-184.
[9]柯凤琴,唐世星.基于MATLAB二级行星轮边减速器可靠性优化设计[J].机械传动,2017,41(7):54-61.
[10]Ou Z,Song C,Zhu C,et al.Dynamic response analysis for NW planetary geartransmission used in electric wheel hub[J].IEEE Access,2019,7:111879-111889.
[11]黄行蓉,刘久周,李琳.基于非线性模态的复杂系统动力学特性分析方法[J].北京航空航天大学学报,2019,45(7):1337-1348.
[12]龚光军,董玉德.有限元法及CAE技术在现代机械工程中的应用探析[J].西安文理学院学报(自然科学版),2017,20(6):36-39.
[13]余丽,伍哲,施冠羽,等.SolidWorks应用于«机械设计课程设计»课程教学[J].机械设计与制造:1-4[2023-11-03].
[14]He,Gai,Wu.Simulation of train–bridge interaction under wind loads:a rigid-flexible coupling approach[J].International Journal Of Rail Transportation,2018,6(3):163-182.
[15]TB/T 3099-2004/XG1—2007,轨枕螺栓机动扳手通用技术条件[S].
[16]赵正大,寸文渊,钱进,等.飞机管道疲劳性能仿真分析与试验验证[J].噪声与振动控制,2023,43(5):239-244,279.
[17]关文信.基于SolidWorks某水下航行器壳体有限元分析[J].机电工程技术,2020,49(11):131-133.
[18]吴哲,张中弛,杨春梅,等.压辊悬臂机床设计与研究[J/OL].林业机械与木工设备:1-6[2023-10-31].
[19]师汉民.机械振动系统:分析测试建模对策[M].武汉:华中科技大学出版社,2004.
[20]薄仕文,李耀翔,王海滨.灌木切割试验装置切割振动分析[J].森林工程,2022,38(5):75-82.
[21]靖娟,王友华.汽车轮毂模态及刚度性能有限元分析[J].汽车实用技术,2023,48(19):112-115.
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/79167.html