摘要:在构建自动导向小车AGV的结构及运动学模型时,由于建模方式不同,机体坐标系原点选择不同,前驱/后驱和前轮/后轮转向都会导致运动学模型结果不一致,精度较差。因此设计了AGV控制系统并对相关参数进行选取和计算;建立车辆运动学模型并在此基础上设计了AGV导航系统及导航算法,采用MPC优化算法提高轨迹跟踪精度。开展了仿真实验验证,对比AGV控制系统的性能和可靠性。结果表明,改进后的MPC模型在提高轨迹跟踪精度方面的表现比传统控制器模型及其他轨迹跟踪方法效果要好,证明所提方法能够提升车辆行驶的轨迹跟踪控制精度,具有很高的实用价值。
关键词:AGV小车,MPC最优化模型,控制变量,状态量
0引言
现代化工业提倡高效、快速、可靠,提倡将人从简单的工作中解放出来。机器人逐渐出现在各个工作岗位上。机器人具有可编程、可协调作业和基于传感器控制等特点,自动导向小车(Automated Guided Vehicle,AGV)是移动机器人的一种,是现代化工业物流系统中的重要设备,主要为储运各类物料,为系统柔性化、集成化、高效运行提供了重要保证。随着科学技术的不断发展,自动导引小车已经成为工业自动化生产中一个重要组成部分,具有降本增效、提高安全性和生产效率等显著的优势。AGV小车控制系统的设计及导航算法研究是实现AGV小车自主导航和自主控制的关键技术,对于提高AGV的性能和应用范围具有重要意义。
当前,在AGV领域,大多采用差速驱动的方式,在转向控制方面具有优势。后轮驱动、前轮转向结构的AGV也是比较常见的,它在控制方面与一般车辆的控制有相似之处,AGV差速驱动难度大,具有深入研究的价值。针对AGV导航控制过程中,存在多变量、非线性、时变系统的难题。本文经过查找相关文献[1-15]基本了解到AGV导航控制的现状;针对前轮转向-后轮驱动的AGV导航控制,提出了MPC控制算法。本文采用模型预测控制(Model Predictive Control,MPC)使AGV控制系统能够实现复杂环境自主导航和自主控制,并且具有较高的安全性和性能。还提出一种基于实际场景的导航控制算法,为后续的研究提供理论支持,为工业自动化生产的实际应用提供新的解决方案。
1 AGV结构及运动学模型
1.1 AGV组成部分
AGV小车通过电脑来控制行进路线以及行为,或利用电磁轨道来设立其行进路线。其结构主要由车体、蓄电池和充电系统、驱动装置、转向装置、精确停车装置、运动控制器、通信装置、移栽系统和导航系统等组成[1]。
与传统搬运车相比,AGV小车具备行动灵活、效率高、运维便捷、功能丰富、安全性强等特点。在搬运过程中,AGV不需要任何铺设轨道或者支座架等固定装置,可以不受场地、道路的影响。满足自动化物流系统的柔性和自动性需求,帮助企业真正意义上提供高效、经济的无人化生产[2]。常见的AGV导航方式包括电磁导航、磁条导航、二维码导航、激光导航、自然轮廓导航、视觉导航等。
1.2运动学模型
(1)建模方法
建模方式不同,机体坐标系原点选择不同,前驱/后驱和前轮/后轮转向都会导致运动学模型结果不一致。复杂的模型并不一定是最好的选择,对车辆运动学模型进行合理简化并且选择行使工况的约束条件才是研究的重点,能够表达控制对象的真实物理限制即可。
阿克曼转向几何(Ackerman Turning Geometry)是一种为了解决交通工具转弯时,内外转向轮路径指向的圆心不同的几何学,可以认为左前轮和右前轮的偏角为同一角度,且瞬时转向中心相交于一点。根据这个原理,可以将四轮模型简化为两轮(单车)模型。本文根据阿克曼转向几何设计AGV。
(2)以后轴中心为原点的车辆运动学模型推导
将机体坐标系原点定义在后轴中心,平面运动存在3个自由度,即3个状态量:
2基于MPC的AGV控制
2.1状态空间方程
随着控制理论的发展,现代控制理论中的模型预测控制(Model Predictive Control,MPC)逐渐成为一种广泛应用的控制策略。MPC以其在多变量、非线性、时变系统控制中的优越性能而备受关注。在MPC中,控制器的状态空间表达式起着至关重要的作用,决定了控制器的性能和稳定性。MPC控制器的状态空间表达式可以通过建立系统的状态空间模型来获得。状态空间模型是描述系统动态行为的数学模型,由一组状态方程和输出方程组成。
状态方程通常由系统的动力学方程确定,可以是线性或非线性的。对于线性系统,状态方程可以用矩阵形式表示如下:
x(k+1)=Ax(k)+Bu(k)(11)
式中:x(k)为系统在k时刻的状态向量;A为状态转移矩阵;B为输入转移矩阵;u(k)为在k时刻的输入向量。状态转移矩阵A描述了系统状态的演化规律,输入转移矩阵B描述了输入对系统状态的影响。
输出方程描述了系统输出与状态之间的关系,通常采用线性方程的形式表示。在MPC控制器中,输出方程用于计算系统的输出值,并与期望输出进行比较,从而确定控制器的控制策略。输出方程通常由系统的观测方程确定,可以是线性或非线性的。对于线性系统,输出方程可以用矩阵形式表示如下:
y(k)=Cx(k)+Du(k)(12)
式中:y(k)是系统在时间k的输出向量,C是输出矩阵,D是直接转移矩阵。输出矩阵C描述了状态与输出之间的线性关系,直接转移矩阵D描述了输入对输出的直接影响。
通过将状态方程和输出方程组合起来,可以得到MPC控制器的状态空间表达式:
x(k+1)=Ax(k)+Bu(k)(13)
y(k)=Cx(k)+Du(k)(14)
MPC控制器的状态空间表达式可以用于设计控制器的参数,如状态反馈增益矩阵和预测模型。通过调整控制器的参数,可以优化控制器的性能和稳定性。控制器的状态空间表达式也可以用于分析控制系统的稳定性和鲁棒性。
2.2预测模型
2.2.1车辆运动学模型
根据几何关系,x、y方向的位移速度为:
x′=v cosφ(15)
y′=v sinφ(16)
根据图(1)中前轴中心的速度三角形,ve为车辆绕着后轴中心转动的线速度,即导致φ变化的线速度,则有:
(3)实施一步Uk(从t=k运行到t=k+1即可)。
下一次从t=k+1时刻重复步骤(1)到(3),重新预测Uk+1,…,Uk+N+1的输入,即每轮的预测都是预测区间和控制区间整体右移一个单位,整个过程在MATLAB中是向右滚动,称为滚动优化控制(Receding Horizon Con⁃trol),系统对控制器的计算能力要求高。
2.2.3 MPC最优化建模
建立二次规划模型,基于二次规划(Quadratic Pro⁃gramming)模型,可通过调用MATLAB、Python等二次规划函数求解,本文基于MATLAB的quadprog函数求解。
已知系统模型X(k+1)=AX(k)+BU(k),输出Y=X,参考目标R=0。式中:X(k+1)为k+1时刻的状态变量;X(k)为k时刻的状态变量;U(k)为k时刻的输入变量。
在k时刻:
(1)设U(k+1|k)表示在k时刻预测的k+1时刻的输入值,在预测区间N内,有
2.2.4约束条件
MPC控制器的约束条件设计是至关重要的,需要考虑多个方面,包括系统的物理特性、控制器的性能要求以及实际应用场景等。在MPC控制器设计中,它们对于控制器的性能和稳定性具有重要影响。首先,MPC控制器的设计目标是在满足系统动态响应和抑制噪声等要求的情况下,使控制对象的状态在约束条件下达到最优。在MPC控制器中,约束条件是通过将其表示为线性或非线性不等式约束来限制控制变量的值。
其次,MPC控制器的约束条件设计需要考虑以下因素:
(1)控制变量的实际操作范围:在确定约束条件时,需要考虑实际操作范围内控制变量的上下限。这些上下限通常由设备厂家提供,并可以考虑传感器误差和控制器系统误差来进行调整。
(2)控制变量的可变性:控制对象的控制变量通常是随时间变化的,因此约束条件应该是可变的。这意味着MPC控制器需要针对每个时间步长重新计算约束条件。
(3)约束条件的优先级:在某些情况下,约束条件可能会相互冲突。例如,在控制温度时,过热和过冷的约束条件可能会冲突。在这种情况下,可以为约束条件分配优先级,以确保最重要的约束条件始终得到满足。
(4)约束条件的复杂度:约束条件的复杂度会影响MPC控制器设计的难度和计算成本。因此,应该尽可能简化约束条件的表达式,以便在实时控制中使用。
总之,MPC控制器约束条件设计是控制器性能和稳定性的关键因素,应该基于实际操作范围、控制变量的可变性、约束条件的优先级和复杂度来进行设计和优化。同时,还需要考虑计算成本,以确保性能和实时性的平衡。
2.2.5优化
本节将介绍MPC中常用的优化算法,并探讨其在实际应用中的一些挑战和解决方案。
Model Predictive Control(MPC)是一种广泛应用于工业自动化领域的控制策略。它通过对系统模型进行预测,并通过优化算法来选择最优控制策略。
MPC中的优化算法是实现控制策略优化的关键[5]。本文基于模型预测控制(MPC),应用于AGV(自动导航车)控制,设计了AGV控制系统并对预测时域、目标轨迹、仿真时间等相关参数进行选取和计算;建立车辆运动学模型并在此基础上设计了AGV导航系统及导航算法,采用MPC优化算法提高轨迹跟踪精度。通过现场实验与仿真结果对比,拟合程度有明显提升,表明改进后的MPC模型在提高轨迹跟踪精度方面的表现比传统控制器模型及其他轨迹跟踪方法效果要好一些,因此本文所提方法能够提升车辆行驶的轨迹跟踪控制精度,并具有很高的实用价值。
3仿真
当使用基于模型预测控制(MPC)的自动导引车(AGV)导航控制时,仿真过程的参数选择是至关重要的。基于MPC的AGV导航控制仿真过程所需要的基本参数如下:
(1)预测时域(Prediction Horizon),这是MPC优化过程的时间范围,通常表示为Np。预测时域的选择应根据AGV的速度、加速度和所需的定位精度来确定。
(2)目标轨迹(TargetTrajectory),这是AGV需要跟随的轨迹,可以是预先设定的路径或动态生成的轨迹。目标轨迹的选择应根据实际应用场景来确定。
(3)仿真时间(Simulation Time),这是仿真过程的总时间,可以根据需要进行设置。仿真时间的选择应足够长,以便充分评估MPC控制器的性能。
上述MPC优化过程的关键参数根据AGV的速度、加速度和所需的定位精度来确定,然后再根据AGV导航控
·73
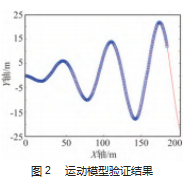
制应用场景和需求进行调整和优化。通过对AGV小车的模型进行仿真控制计算,将其运动学模型的输出参数为大地坐标系下位移的变化率(速度)和航向角的变化率(航向角速度),前轮偏角和后轮速度为模型的输入参数,严格按照公式编写状态更新函数,其函数验证时给定恒定速度和正弦变化的前轮偏角,验证结果如图2所示。
如图2所示,采用模拟预测控制(MPC)的AGV(自动引导车),模拟轨迹与目标轨迹基本完全重合,控制精度相较于其他控制系统有较大提升,定位精度较高,本模拟控制方法具有较高的使用价值。
4结束语
本文根据实际场景选择对应的模型,采用建模方式、机体坐标系原点选择、前驱/后驱、前轮/后轮转向等集中模型分析了导致运动学模型结果的不一致原因。这些集中模型对复杂的模型并不一定是最好的选择,本文对车辆运动学模型进行合理简化,并且选择行使工况的约束条件下,确定了表达控制对象的真实物理限制,并在推导过程中进行运动学建模,给出了机体坐标系和大地坐标系的转换不同模型。
通过机体坐标系原点设置为质心或前/后轴中心,对车辆方位坐标、角度等的变换进行了推导、仿真分析和实验验证,结果展示采用MPC模型的AGV小车在轨迹跟踪的过程中,模拟轨迹与目标轨迹基本完全重合,控制精度相较于其他控制系统有较大提升,定位精度较高。
因此改进后的MPC模型在提高轨迹跟踪精度方面的表现比传统控制器模型及其他轨迹跟踪方法效果要好,证明所提方法能够提升车辆行驶的轨迹跟踪控制精度,具有很高的实用价值。
参考文献:
[1]孙国正.面向21世纪的物流工程及物料搬运技术[J].中国远洋航务公告,2001(1):53-55.
[2]孙旖.现代物料搬运及其发展趋势[J].河北煤炭,2002(4):16-28.
[3]冯星华.AGV及其控制系统研制[J].电子机械工程,2001(1):31-33.
[4]李峥峰,张东方,丁其聪,等.考虑AGV运输和机器转速的作业车间绿色调度研究[J].机电工程,2024,41(2):327-336.
[5]龚霞,黄鑫,杨章沐,等.基于MPC的智能小车轨迹跟踪控制器的研究[J].轻工科技,2019,35(10):41-42.
[6]郝西祥,陈亚伟,邵毅明.基于非线性MPC方法的车辆稳定性控制[J].重庆理工大学学报(自然科学),2019,33(2):27-32.
[7]tingfenghanlei.模型预测控制[EB/OL].(2018-12-17).https://blog.csdn.net/tingfenghanlei/article/details/85046120.
[8]AdamShan.无人驾驶汽车系统入门(十)——基于运动学模型的模型预测控制[EB/OL].(2018-01-17).https://blog.csdn.net/AdamShan/article/details/79083755.
[9]胡寿松.自动控制原理[M].6版.北京:科学出版社,2013.
[10]王琳华.磁导式AGV自动导航车控制系统的设计[D].长沙:长沙理工大学,2013.
[11]于洋.AGV及其控制器设计与开发[D].杭州:浙江大学,2008.
[12]胡彬.面向柔性制造系统的无人搬运车控制器研究[D].上海:上海交通大学,2012.
[13]王冰,胡彬,王春香,等.自动导引车车载控制系统的研究与设计[J].自动化仪表,2013,34(5):1-4.
[14]叶程洋,夏继强.双转向架驱动AGV的分布式控制系统设计[J].仪表技术与传感器,2015(9):67-69+76.
[15]GB/T 30030—2013,自动导引车(AGV)术语[S].
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/78172.html