SCI论文(www.lunwensci.com)
摘要:在科学研究和工业应用的复杂流域、多相流以及多物理流动问题的处理中,相较于传统计算流体力学方法(Computational Fluid Dynamics,CFD),格子玻尔兹曼算法(Lattice Boltzmann Method,LBM)具有程序结构简单、对复杂边界和非线性问题适应性强以及便于并行计算等诸多优点。然而,其作为一种显式算法,在计算过程中的迭代次数较多,进而消耗大量计算资源。利用神经网络在预测与回归方面的强大能力,基于LBM设计了一个具备单隐藏层的浅层人工神经网络预测模型并将其命名为ML-LBM(Machine Learning LBM)模型。该模型通过动态调整碰撞算子中不同驰豫时间,以粗化网格来重现精细分辨的参考模拟。对于顶盖驱动流问题,模型完成训练后,对测试集均方误差在6×10-5以下,精度得到了保障。相较于经典LBGK模型,ML-LBM模型的计算效率提升约9倍。
关键词:格子玻尔兹曼算法;碰撞算子;神经网络结构;算法加速
Lattice Boltzmann Method Based on Neural Network
Wei Weixun,He Shengsheng,Huang Zhigang
(School of Mechanical and Electrical Engineering,Guangdong University of Technology,Guangzhou 510006,China)
Abstract:Compared with traditional Computational Fluid Dynamics(CFD),computational fluid dynamics for complex drainage basins,multiphase flows,and multi-physical flow problems for scientific research and industrial applications,the Lattice Boltzmann Method(LBM)has many advantages,such as simple program structure,strong adaptability to complex boundary and nonlinear problems,and convenient parallel computation.However,as an explicit algorithm,it has many iterations in the calculation process,which consumes a lot of computing resources.Based on the powerful ability of neural network in prediction and regression,a shallow artificial neural network prediction model with single hidden layer is designed based on LBM and named as ML-LBM(Machine Learning LBM)model.The model reproduces the reference simulation of fine resolution by coarsening the mesh by dynamically adjusting the different relaxation times in the collision operator.For the problem of the top drive flow,the mean square error of the test set is less than 6×10-5 after the model is trained,and the accuracy is guaranteed.Compared with the classical LBGK model,the computational efficiency of ML-LBM model is improved by about 9 times.
Key words:lattice boltzmann method;collision operator;neural network structure;algorithmic acceleration
0引言
计算流体动力学(Computational Fluid Dynamics,CFD)在科学研究和工业应用中发挥着重要的作用。与基于宏观流体力学Navier-Stokes方程的传统CFD方法不同,格子玻尔兹曼方法(Lattice Boltzmann Method,LBM)是基于动理学玻尔兹曼方程的介观方法[1],因此具有许多独特的优点,例如流体粒子碰撞和流动过程清晰,边界条件易于施加,不涉及偏微分方程离散等,这些特点使LBM成为流体模拟的强大工具。LBM作为一种新的计算方法,近30年来得到了极大的发展[2-3]。然而,LBM作为一个全显式算法,为了保证计算的稳定性以及精度,其每次计算的时间步长很短,而较短的时间步长导致计算迭代次数增多,使得对计算资源的消耗较高。因此,计算效率始终是制约LBM应用的最大问题之一。
虽然使用GPU服务器以及并行计算,能有效提升LBM的计算效率[4],但对于大规模的研究依然负担过重。同时高性能的GPU服务器在家用平台的研究中亦不常见。机器学习(Machine Learning,ML)的兴起,为高效CFD计算打开了新的思路[5-7]。同时LBM可以直接用矩阵运算的形式表示,其数据结构和计算方式,与神经网络之间具有很好的相容性,特别适合进行机器学习增效。
机器学习结合LBM更多的是针对特定应用的研究,主要是利用LBM生成的模拟结果,对神经网络进行训练。并直接由初始工况条件和边界设定预测最终的目标特征量,计算效率非常高。Rutgers等[8]将深度学习应用到LBM模拟中,预测物体引起的声压变化。Rabbani等[9]基于截面图像训练人工神经网络,对多孔岩石的渗透率进行了预测,其结果与LBM的计算结果高度相符。San⁃tos提出了一种3D卷积神经网络[10],可以根据岩石图像,快速准确地对其中的流动进行预测。李佳[11]对基于机器学习的多孔介质渗透率预测进行了研究。Wang等[12]根据多孔介质的LBM模拟数据集,训练了一个卷积神经网络对渗透率进行估算,准确率超过90%。严格来说,以上研究并不完全是根据格子玻尔兹曼方法的机器学习增效。因为学习过程忽略了其他相关物理量的信息,脱离了LBM算法的本质,训练数据既可以由LBM生成,也可以通过其他CFD方法得到。
近年来,也有许多国内外学者对机器学习LBM基础模型方面展开了大量研究。本文参考了相关文献对机器学习LBM基础模型方面的研究[13-16],提出一个ML_LBM模型,在神经网络中引入物理信息,通过学习局部碰撞算子,在粗化网格上使用神经碰撞算子替代了精细网格上的经典BGK(Bhatnagar Grook Krook)碰撞模型。最后,对顶盖驱动流算例进行仿真测试验证,结果表明:与传统LBGK模型相比,在保证模拟精度的同时,ML_LBM模型亦体现出更快的计算速度。
1 LBGK模型
2基于神经网络的ML_LBM模型
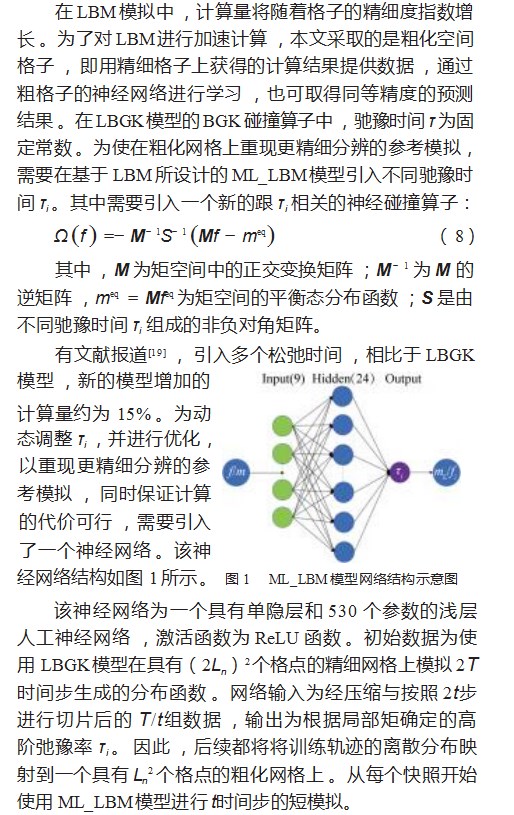
2.1模型网络结构
2.2 ML_LBM模型损失函数与优化
损失函数是模型训练过程评判模型训练优劣的工具,常使用的是L2的损失函数均方误差(Mean Squared Error,MSE)。
本文中训练采用反向传播算法(back propagation)。即对于每一个实例而言,反向传播算法首先进行预测(正向传递),并测量保留误差,然后反向经过每个层以测量来自每个连接处的误差贡献(反向传递),最后调整连接权重以减少错误(梯度下降步骤),具体步骤如下。
(1)分布函数前向传播到输出层,利用损失函数评估精细网格生成的分布函数与在粗化网络上使用网络输出的Ti组成的神经网络碰撞算子模拟生成的分布函数的误差。
(2)误差反向传递基于梯度下降策略,以目标的负梯度方向对参数进行调整。
(3)通过链式求导法则求梯度,对超参数如μi等进行调整。
(4)反向传播过程:把误差当作输入向量,网络传播方向反向,误差层级反向传播同时根据梯度下降法更新参数值。
本文中利用的优化算法为自适应动量的随机优化方法中的Adam优化算法。
3算例实验
3.1模型训练
本文设计用以证明模型有效性的算例为顶盖驱动流。顶盖驱动流常被运用于计算流体力学算法的验证中[20],其原因主要是其流场特点十分鲜明,便于结果之间进行比对;其次顶盖驱动流问题的边界条件和初始条件简单,程序设计较为简便。算例的上侧为速度边界,左右及底部为无滑移碰撞边界。顶盖驱动流问题虽是一个稳态问题,但由于本文关注的是神经网络模型对LBM演化的整体加速效果。因此整个流场演化过程皆为本实验关注的重点,而非仅仅关注计算最终的稳态效果。
3.2精度误差分析
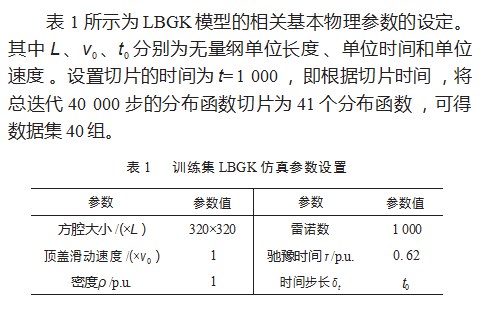
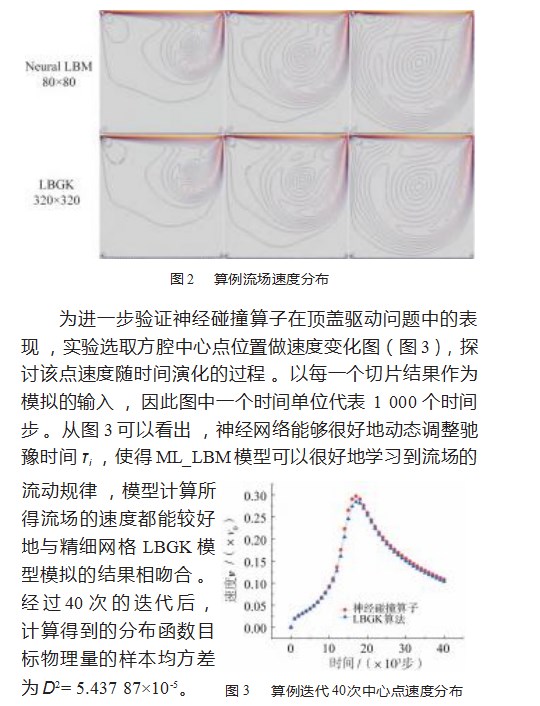
下面在实际的实验当中调用模型测试,验证模型的性质。分别选取原始时间t=10 000、t=20 000、t=30 000时间步时的流场速度分布情况,对于采用经典LBGK模型来说,缩放分辨率后的ML_LBM模型的表现非常不错,计算结果如图2所示。第一行为粗化网格ML_LBM模型计算结果,第二行为精细网格LBGK模型计算结果。直观说,神经网络模型几乎与LBGK模型的计算发展完全一致。
3.3计算效率分析
本实例中ML_LBM模型的目的在于重现顶盖驱动流在精细分辨下的LBM模拟,且已成功实现。因此若将该模型泛化于其他一些不需要很高精度且对计算速度有一定要求的算例当中,则需要对该模型的计算速度进行一个评估。
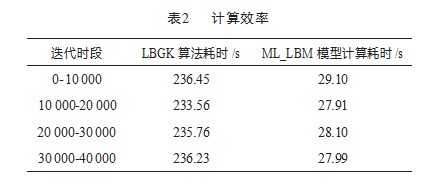
本实验测试平台参数:CPU为AMD Ryzen 5 4600H;GPU为NVIDIA GeForce GTX 1660 Ti。这一平台属于典型的家用机硬件配置,该测试环境有利于模拟本模型在计算机性能受限制情况下的计算能力。实现模型算法的语言环境为Python3.7,使用的深度学习框架为PyTorch。由于本文的LBM加速方法为粗化空间格子,因此常用的对LBM方法运算表现的评判标准每秒百万格子更新数MLUPs已不再适用。从调用模型计时来测定神经网络模型的加速效果。以不同时段分别利用ML_LBM模型完成计算和原有算法LBGK模型计算的耗时对比作为参考,时段则由完成的迭代时间步表示,测试结果如表2所示。从表中可以看出,原有算法LBGK模型的计算耗时为ML_LBM模型的9倍左右。
由此可见,在家用级别平台上,相较于LBGK模型,本文所使用的ML_LBM模型误差在保证精度阈值内,减小计算资源消耗、降低计算时间方面效果显著,该算法的实验结果达到预期。
4结束语
为提高LBM的计算效率,本文实现对LBM原有网格的粗化过程,克服LBM在消耗计算资源方面的劣势。基于上述目标,本文利用神经网络设计了一个预测网络模型并定义为ML_LBM模型。该模型通过输入精细网格的粒子分布函数数据对粗化网格上迭代t步的粒子分布函数进行预测,并设计了一个包含物理信息的损失函数,在一定程度上提高了模型的精度。完成模型训练后,本文对该模型预测精度以及计算效率进行了分析与验证。其结果表明,本文所提出的模型能够在保证精度较高的同时,实现很大程度的加速。
参考文献:
[1]T Kruger,H Kusumaatmaja,A Kuzmin,et al.The lattice Boltzmann method:principles and practice[J].Cham,Switzer⁃land:Springer International Publishing AG,2016.
[2]薛海虹,王政道,钱跃竑.格子Boltzmann方法处理复杂边界新进展[J].力学季刊,2016,37(4):615-624.
[3]李旭晖,单肖文,段文洋.格子玻尔兹曼正则化碰撞模型的理论进展[J].空气动力学学报,2022,40(3):46-64.
[4]Sl A,Ms A,Mg A,et al.Towards real-time simulation of turbu⁃lent air flow over a resolved urban canopy using the cumulant lat⁃tice Boltzmann method on a GPGPU[J].Journal of Wind Engi⁃neering and Industrial Aerodynamics,2019,189:151-162.
[5]Molemaker J,Cohen J,N Patel S,et al.Low viscosity flowsimula⁃tions for animation,eurographics/acm[C]//Siggraph Symposium on Computer Animation,2008.
[6]Lentine M,Wen Z,Fedkiw R.A novel algorithm for incompress⁃ible flow using only a coarse grid projection[J].Acm Transactions on Graphics,2010,29(4CD):1-9.
[7]Cheng,Yang,Xubo,et al.Data-driven projection method in fluid simulation[J].Computer Animation&Virtual Worlds,2016.
[8]R Mario,S R Koh,J Jitsev,et al.Prediction of Acoustic Fields Us⁃ing a Lattice-Boltzmann Method and Deep Learning[J].High Performance Computing,2020.
[9]A Rabbani,M Babaei.Hybrid pore-network and Lattice-Boltzmann permeability modelling accelerated by machine learn⁃ing[J].Advances in Water Resources,2019,126(APR.):116-128.
[10]J E Santos,D Xu,H Jo,et al.PoreFlow-Net:A 3D convolution⁃al neural network to predict fluid flow through porous media[J].Advances in Water Resources 2020,138:103539.
[11]李佳.基于机器学习的多孔介质渗透率预测研究[D].杭州:浙江大学,2019.
[12]Y D Wang,T Chung,R Armstrong,et al.ML-LBM:Machine Learning Aided Flow Simulation in Porous Media[J].arXiv:2004.11675.
[13]Hennigh.Lat-Net:Compressing Lattice Boltzmann Flow Simu⁃lations using Deep Neural Networks[J].arXiv preprint arXiv:1705.09036 2017.
[14]X Y Chen,G C Yang,Q H Yao,et al.A compressed lattice Boltzmann method based on ConvLSTM and ResNet[J].Comput⁃ers&Mathematics with Applications,2021,97:162-174.
[15]M C Bedrunka,D Wilde,M Kliemank,et al.Lettuce:Pytorch-based lattice boltzmann framework[J].High Performance Com⁃puting,2021,12761:40-55.
[16]Prins,H M Joost.Lattice Boltzmann method with a neural net⁃work collision operator[D].Eindhoven:Eindhoven University of Technology,2022.
[17]Y H Qian,D d′Humières,P Lallemand.Lattice BGK models for Navier-Stokes equation[J].Euro-physics Letters(EPL),1992,17(6):479-484.
[18]GUO Z,ZHENG C.Theory and applications of Lattice oltzmann method[M].Beijing:Press Science,2009.
[19]Dominique D′Humières,Ginzburg I,Krafczyk M,et al.Multi⁃ple-relaxation-time lattice Boltzmann models in three dimen⁃sions[J].Philosophical transactions.Series A,Mathematical,physical,and engineering sciences,2002,360(1792):437-51.
[20]SHANKAR P N,DESHPANDE M D.Fluid mechanics in the driven cavity[J].Annual Review of Fluid Me⁃chanics,2000,32(1):93-136.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/77430.html