SCI论文(www.lunwensci.com)
摘要:为解决多机器人协作焊接路径规划方法需要搜索效率高和寻优精度高的问题,采用性能较优的哈里斯鹰优化算法建立基于寻找最佳初始焊接位置的多机器人协作焊接路径规划方法,仿真实验证明哈里斯鹰算法能够很好地寻找出最佳初始焊接位置和关节变化稳定的路径,但在多机器人协作焊接路径规划时容易陷入局部最优的问题,因此提出一种提高克服局部最优能力的改进哈里斯鹰优化算法。其中采用3种不同的策略对哈里斯鹰优化算法进行改进:首先采用拉丁超立方抽样策略对种群初始化进行优化;再采用自适应更新因子策略更新r1和r3;最后采用随机飞行策略进行对最佳个体进行位置偏离。利用仿真平台结合两种算法对多机器人协作焊接路径规划各自独立仿真运行30次,并进行结果比较。结果表明相对于原哈里斯鹰优化算法,改进哈里斯鹰优化算法在多机器人协作焊接路径规划中不仅具有更强的克服局部最优能力,还具有很好的收敛精度和收敛速度。
关键词:多机器人协作;改进哈里斯鹰算法;最佳初始焊接位置
Multi-robot Cooperative Welding Path Planning Based on Improved Harris Eagle
Optimization Algorithm
Wang Hongmin1,Li Jiangyuan1,Jiang Meng1,Liang Jingbin1,Wu Longhua1,Song Yingying1,Pan Zengxi1,2
(1.Faculty of intelligent Manufacturing,Wuyi University,Jiangmen,Guangdong 529020,China;
2.University of Wollongong,Wollongong,Australia)
Abstract:To solve the problems of high search efficiency and optimization accuracy in the planning method of multi robot collaborative welding paths,the Harris Eagle optimization algorithm with better performance is adopted to establish a multi robot collaborative welding path planning method based on finding the optimal initial welding position.Simulation experiments show that the Harris Eagle algorithm can effectively find the optimal initial welding position and the path with stable joint changes.However,it is prone to getting stuck in local optima during multi robot collaborative welding path planning.Therefore,an improved Harris Eagle optimization algorithm is proposed to improve the ability to overcome local optima.Among them,three different strategies are used to improve the Harris Eagle optimization algorithm:first,the Latin hypercube sampling strategy is used to optimize the population initialization,and then the adaptive update factor strategy is used to update r1 and r3;a random flight strategy is adopted to perform position deviation on the optimal individual.Using a simulation platform combined with two algorithms,the multi robot collaborative welding path planning is simulated and run 30 times independently,and the results are compared.The results show that compared to the original Harris Eagle optimization algorithm,the improved Harris Eagle optimization algorithm not only has stronger ability to overcome local optima in multi robot collaborative welding path planning,but also has good convergence accuracy and speed.
Key words:multi-robot cooperation;improved Harris Eagle algorithm;optimal initial welding position
0引言
多机器人协作系统是目前机器人应用的一个重要发展方向,相比于单机器人系统,多机器人协作系统不仅具有解决复杂性任务、提高系统的鲁棒性和可靠性等优势,还已经成功应用于焊接和协作搬运等领域;但是这些任务目前大部分还是由人工示教的方式来实现,缺乏自主运动规划的能力[1-3]。而随着国家提出的智能化生产要求,多机器人协作系统应具备自主规划运动的能力,故研究多机器人协作系统的运动规划问题是十分必要的。
路径规划在多机器人的生产实践中占据着重要地位,其目的主要在复杂的工作环境中规划出一条初始点到工作点的最佳路径,确保机器人在无碰撞等条件下安全完成任务。目前智能仿生算法是已存在的多机器人路径规划算法的重要一种,如遗传算法[4]、粒子群算法[5]和蚁群算法[6]等,智能仿生算法有着计算量低和优化效率高等特点[7]。因此智能仿生算法为解决多机器人路径规划问题提供了新思路。
哈里斯鹰优化算法[8]一经提出,得到广大学术界的关注。文献[9]将人工生态系统的优化算法(AEO)和哈里斯鹰优化算法(HHO)进行杂交,并使用局部搜索机制和混沌理论等来提高算法的勘探开发能力。文献[10]利用混沌方法、柯西突变增加种群多样性来有效限制算法进入局部最优,利用精英指导策略指导种群个体位置更新来加快算法收敛速度。文献[11]使用新的转换策略来改善算法中探索和开发之间的转变效率,使用改进的微分扰动和贪婪策略代替原来的开发过程去提高算法的全局搜索能力。文献[12]融入一种突变的方法为每次迭代创造一个多样化的解空间的方法来克服HHO算法容易陷入局部最优的缺点。文献[13]利用混沌映射和勘探因子来提高种群的多样性和勘探能力,还使用随机游走策略进一步提高HHO的开发能力。文献[14-15]通过多种策略成功优化哈里斯鹰优化算法,并成功应用于路径规划上。
在面对使用哈里斯鹰优化算法对多机器人协作焊接路径规划容易陷入局部最优的问题,受文献[11-15]的启发影响,本文提出一种针对提高克服局部最优能力的改进哈里斯鹰优化算法。首先在算法初始化阶段利用超立方抽样策略将种群均匀分布各个空间,以此来提高种群初始化质量;然后在能量衰减过程中采用自适应更新策略更新r1和r3,以此来提高算法的勘探能力;最后采用随机飞行策略对每次能量衰减迭代后最佳个体进行偏离,以此来提高种群多样化,从而提高算法的勘探能力。通过两种算法仿真结果比较,改进哈里斯鹰优化算法相比于哈里斯鹰算法不仅提高了克服局部最优能力,还提高了收敛精度和收敛速度。
1多机器人协作焊接系统运动学分析
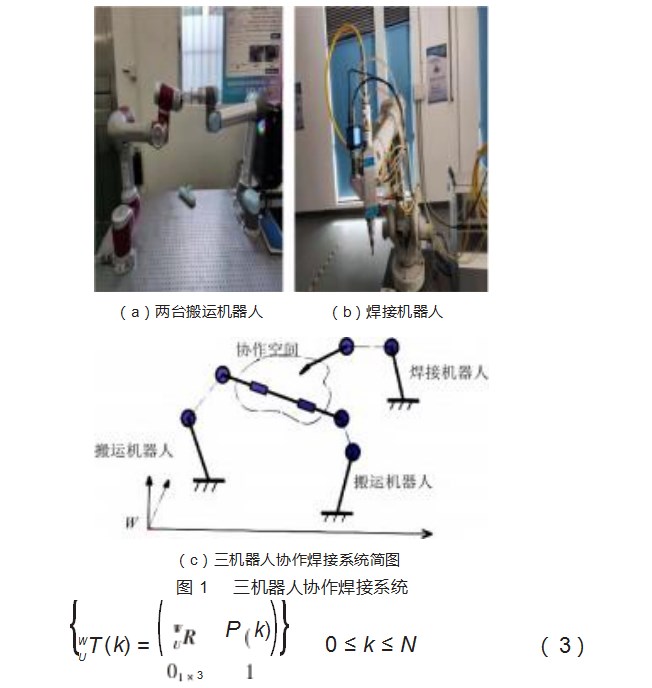
根据实验室搭建的双机器人平台(UR5和JAKAZu7)以及后面购买的伯朗科机器人(BRTIRUS1510A)来建立的多机器人协作焊接系统,具体如图1所示,其中双机器人作为搬运机器人,伯朗科机器人作为焊接机器人。设定3个机器人对同一个刚体进行协作焊接时,各个机器人的基座是固定的,则从各个机器人基坐标系{B}到世界坐标系{W}的齐次变换矩阵T为固定值。
设定双搬运机器人共同夹持工件保持姿态不变做直线运动,因此工件坐标系{U}会不断变化,以世界坐标系{W}为参考,故得工件初始位姿和目标位姿分别如式(1)和式(2)表示:
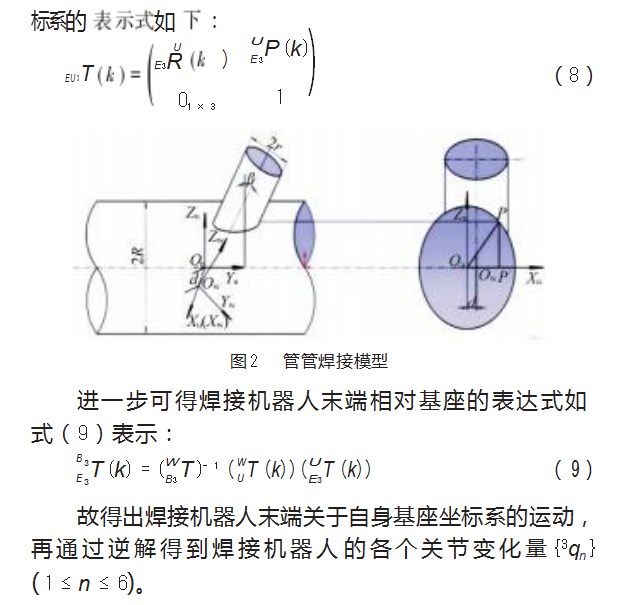
焊接机器人采用的是一种应用于管管相贯曲线的焊接方法[16],根据文献[16]建立的管管焊接模型如图2所示,{U}为机器人工件坐标系(主管坐标系),{V}为从管坐标系,主管半径为R,从管半径为r,{V}相对于{U}的偏距为d,偏角为β。但由于本文采用的是马鞍形焊接,因此偏距d和偏角β都为零。同时由于焊接机器人与搬运机器人动作协同,因此需将马鞍形焊缝均分为N等分,即将[0,2π]分为N份,则∆φ=2π/N,因此产生N+1个焊缝点φk=k∆φ(0≤k≤N)。最终可得欧拉角公式和位置公式如式(6)~(7)所示。
本节通过建立起多机器人协作焊接模型后,可以求出3个机器人的关节变化,为下文建立路径优化函数做铺垫。
2多机器人协作焊接路径规划研究
2.1问题描述
本文仅针对多机器人协作焊接过程中做路径规划,因此采用的思路为寻找最佳初始焊接位置从而规划出各个机器人的路径。可操作度的研究是多机器人协作的重要内容,主要用于改善机器人的传力和传速性能[17-18],传力和速度的稳定性是焊接产品质量的保证;全局关节变化量在多机器人协作过程中在满足任务要求的同时应尽量小[19],这一定程度上能够降低能耗。
多机器人协作焊接系统的初始位置求解不仅需要考虑整体可操作度和全局关节运动量综合最优,还要考虑协作空间、机器人碰撞和和奇异位形等问题。因此建立优化目标函数和约束条件为:
因此最佳初始焊接位置问题就变成求多目标综合最优的问题,搜索需要满足以下约束条件:(1)初始焊接位置和搬运机器人轨迹必须在协作空间S中;(2)各个机器人运动过程中无碰撞发生;(3)尽量远离各个机器人的奇异位形。
2.2焊接仿真
2.2.1空间求解
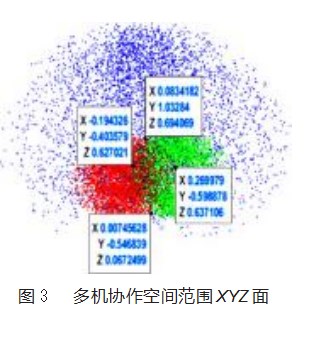
协作空间是多机协作的基础,一旦工件位姿不在协作空间将导致协作任务无法完成,因此在进行多机协作轨迹规划前需要先求解出协作空间。参考文献[20-21]来建模,设置两个搬运机器人的X轴中点为世界坐标系原点,3个机器人基坐标系在世界坐标系中的位置分别为B1={x=-0.2,y=0,z=0}、B2={x=0.2,y=0,z=0}和B3={x=0,y=0.7,z=0}。最终求出的协作空间范围大概为:X∈[-0.19,0.26]、Y∈[-0.54,1.03]、Z∈[0.06,0.69],其中XYZ面如图3所示。
2.2.2路径规划仿真
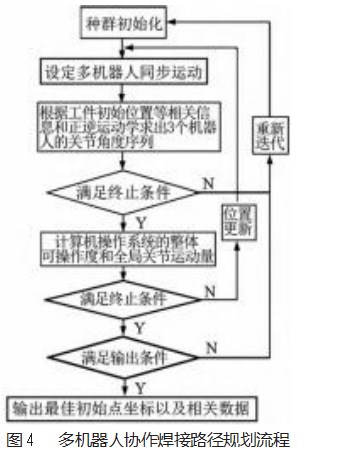
将多机器人协作焊接系统的运动学分析、优化函数和约束条件等参数与哈里斯鹰优化算法结合,多机器人协作焊接路径规划流程如图4所示。本文为了保证优化结果质量,还设置一个循环机制,主要通过多次运行测试,得出一个最低输出阈值。将每次循环完成后得到函数值是与最低输出阈值进行比较大小来判断是否输出,若不小于则输出,若小于则重新赋值重新循环迭代,直至达到输出条件。
2.2.3仿真结果
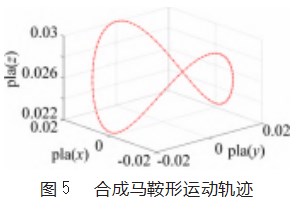
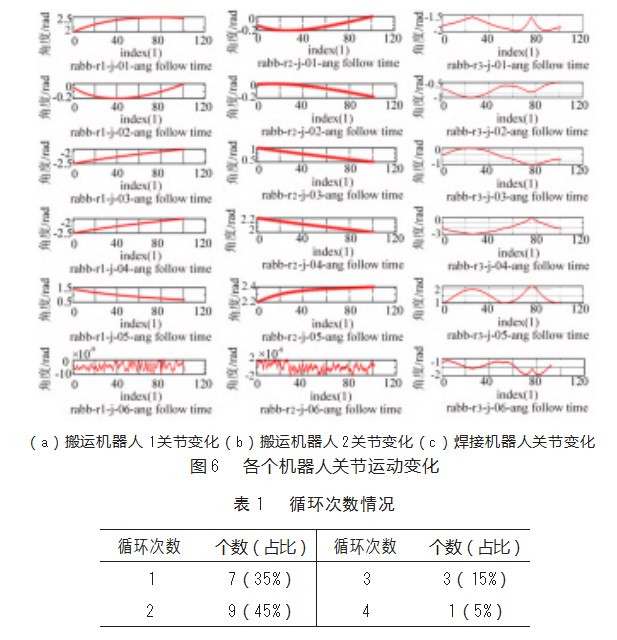
HHO的算法设置参数如下:鹰群规模Q=80,最大能量衰减次数为Tmax=30和路径分段K=100。根据2.2.2节中设定的机器人约束条件和运动学分析建立仿真编程,通过独立仿真20次,其中最好一次优化得到的多机器人协作焊接路径规划的各种数据图如图5~6所示,以及得到一组循环次数的数据如表1所示。由图5可知,多机器人能够协作完成马鞍形焊接和各个机器人的关节运动曲线平滑,表明各个机器人能够灵活地完成任务。但是从表1中得知,循环1次的概率仅有35%。由此可见哈里斯鹰优化算法在多机器人协作焊接路径规划时,虽能找到合适的初始焊接位置使各个机器人能够灵活地完成任务,但是有容易陷入局部最优问题。这种输出效率低的问题明显不符合工程应用上的高效率要求,因此需要改进哈里斯鹰优化算法。
3改进哈里斯鹰优化算法的实现与效果
3.1改进策略
由第2章可知哈里斯鹰优化算法在多机器人协作焊接路径规划中容易陷入局部最优的问题,因此提出一种针对这个问题的多策略改进哈里斯鹰优化算法(IHHO)。采用拉丁超立方抽样方法提高种群初始化质量[22],以及采用自适应方法跟新全局探索因子(r1和r3)和每次迭代更新完后加入采用随机游走策略增大种群多样性。
首先采用拉丁超立方抽样方法提高种群初始化质量。由于多机器人协作空间为3维空间,因此可将协作空间均分为N3块,然后将随机生成的规模为(P×N3)的个体均匀分布到各个板块。采用该方法初始化则可将鹰群均匀分布到整个协作空间,提高鹰群的种群质量和多样性,以此提高算法的克服局部最优能力。
然后采用自适应方法跟新全局探索因子r1和r3,使鹰群在前期能探索更大的范围和后期进行细致的搜索,以此来增大算法前期的全局搜索能力和后期局部搜索能力。建立探索因子更新公式为:
3.2仿真效果对比
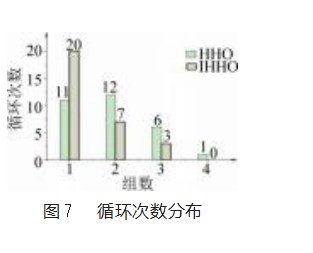
IHHO的算法设置基本参数跟HHO一致,同时设定拉丁超立方抽样分段N=2。两种算法各自独立运行30次,其中得到的输出循环次数分布如图7所示。由图可得改进算法循环1次输出的概率达到66.7%,且循环次数主要集中在2次以内,因此改进哈里斯鹰优化算法克服局部最优能力得到显著提升。
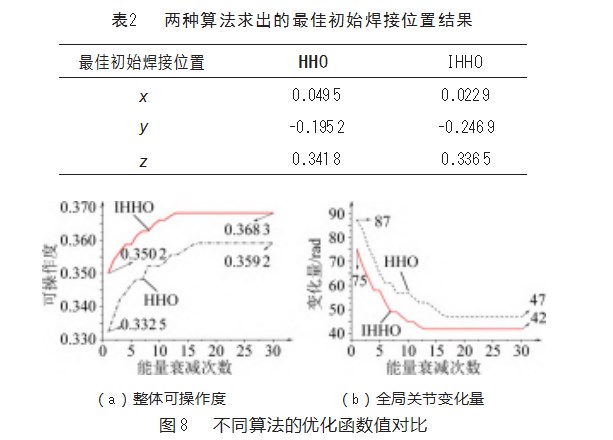
并将每种算法最优的一次仿真结果进行比较,其中两次得出的最佳初始焊接位置如表2所示,目标函数整体可操作度和全局关节变化量随能量衰减变化情况如图8所示。由图可知,相对于HHO算法,全局可操作度初始值与目标值分别提升了5.32%和1.94%;全局关节变化量的初始值降低了13.79%和目标值降低了10.63%;以及收敛速度也有所提高。由此可知,改进算法不仅提高了收敛精度,也一定程度上提高了收敛速度。
4结束语
本文通过采用哈里斯鹰优化算法建立基于寻找最佳初始焊接位置的多机器人协作焊接路径规划,从而解决多机器人协作焊接路径规划方法需要搜索效率高和寻优精度高的问题,通过仿真实验证明基于哈里斯鹰优化算法的多机器人协作焊接路径规划方法效果不错。但存在多机器人协作焊接路径规划时容易陷入局部最优的问题,因此本文提出一种针对提高克服局部最优能力的哈里斯鹰优化算法。仿真结果对比表明,相对于哈里斯鹰优化算法,改进哈里斯鹰优化算法提高了克服局部最优能力,且提高收敛精度和收敛速度。因此表明改进哈里斯鹰优化算法在多机器人协作焊接路径规划具有可行性和有效性,可以为后续的多机器人路径规划的具体实践提供借鉴。
参考文献:
[1]Alaa Khamis,Ahmed Hussein.Ahmed Elmogy et al.Multi-robot Task Allocation A Review of the State-of-the-Art[J].Cooperative Robotsand Sensor Networks.2015(5):31-35.
[2]M Bemardine Dias,Marc Zinck,Robert Zlot,et al.Multirobot Co⁃ordination in Dynamic Environments[J].IEEE Intamational Con⁃ference on Robotics&Automation New Orieans,LA,Aprill 2004,New York:IEEE,2004(4):3435-3442.
[3]甘亚辉,戴先中.基于遗传算法的多机器人系统最优轨迹规划[J].控制理论与应用,2010,27(9):1245-1252.
[4]周红勋.基于多种群遗传算法的多机器人路径规划[J].电子技术与软件工程,2022(9):126-129.
[5]段晋军.多机器人协作焊接中的轨迹规划和位置力协调控制的研究[D].南京:东南大学,2019.
[6]顾军华,孟慧婕,夏红梅,等.基于改进蚁群算法的多机器人路径规划研究[J].河北工业大学学报,2016,45(5):28-34.
[7]龙樟,李显涛,帅涛,等.工业机器人轨迹规划研究现状综述[J].机械科学与技术,2021,40(6):853-862.
[8]Ali Asghar Heidari,Seyedali Mirjalili,Hossam Farisd,et al.Harris hawks optimization:Algorithm and applications[J].Future Gener⁃ation Computer Systems 2019(97):849–872.
[9]Saeid Barshandeh,Farhad Piri,Simin Rasooli Sangani,et al.HM⁃PA:an innovative hybrid multi-population algorithm based on artifcial ecosystem-based and Harris Hawks optimization al⁃gorithms for engineering problems[J].Engineering with Comput⁃ers 2020(7).
[10]Wen Lei,Wang Guopeng,Yue Longwang,et al.Multistrategy Harris Hawks Optimization Algorithm Using Chaotic Method,Cauchy Mutation,and Elite Individual Guidance[J].Hindawi Discrete Dynamics in Nature and Society,2022:5129098.
[11]Zou Lewang,Zhou Shihua,Li Xiangjun,et al.An Efficient Im⁃proved Greedy Harris Hawks Optimizer and ItsApplication to Feature Selection[J].Entropy 2022(24):1065.
[12]Navid Kardani,Abidhan Bardhan,Bishwajit Roy,et al.A novel improved Harris Hawks optimization algorithm coupled with ELM for predicting permeability of tight carbonates[J].En⁃gineering with Computers,2021.
[13]Song Meijia,Jia Heming,Laith Abualigah,et al.Modified Harris Hawks Optimization Algorithm with Exploration Factor and Random Walk Strategy[J].(Hindawi)Computational Intelli⁃gence and Neuroscience,2022:23.
[14]占家豪.改进哈里斯鹰优化算法在路径寻优中的应用[D].杭州:杭州电子科技大学,2022.
[15]林笑笑.基于改进哈里斯鹰算法的物流机器人任务分配和路径规划研究[D].开封:河南大学,2022.
[16]张毅,张旭,罗元.不规则管管相贯曲线的轨迹规划[J].华中科技大学学报(自然科学版),2015,43(S1):276-279,283.
[17]姚建初,丁希仑,战强,等.冗余度机器人基于任务的方向可操作度研究[J].机器人,2000(6):501-505.
[18]刘迎春,余跃庆,姜春福.机器人可操作性研究进展[J].机械设计与研究,2003(4):34-37,7.
[20]王威,许勇,刘勇,等.基于MATLAB的双机器人协作空间求解及分析[J].轻工学报,2019,34(4):102-108.
[21]陶平,邹成文,王天瑞.多机器人协作的灵活性分析与仿真[J].制造技术与机床,2022(7):23-27.
[22]徐杰,鲁海燕,赵金金,等.拉丁超立方抽样的自适应高斯小孔成像蝴蝶优化算法[J].计算机应用研究,2022,39(9):2701-2708,2751.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/77265.html