SCI论文(www.lunwensci.com)
摘要:等几何分析方法作为一种新型数值分析方法得到了广泛关注。针对传统等几何分析过程中,非均匀有理B样条(NURBS)曲线建模存在控制点较多、局部细化薄弱以及多面片拼接导致模型空间连续性较差等问题,提出一种基于PHT样条分层细分的等几何分析(IGA)方法。以某型风力机叶片为研究对象,分析了PHT样条细分对风力机叶片模型求解精度的影响,并通过有限元仿真结果进行对比分析。结果表明:细分前基于NURBS的风力机叶片模型等几何分析结果与有限元结果的相对误差为5.9%,细分后IGA结果与有限元结果的相对误差为3.7%,证明了经过PHT样条细分,风力机叶片的等几何分析求解精度得到了有效提高。提出的方法对后续风力机叶片的数值仿真和优化设计具有一定的参考意义。
关键词:风力机叶片;PHT样条;等几何分析;非均匀有理B样条
Study on PHT Spline Refinement of Wind Turbine Blade Based on
Isogeometric Analysis
Yin Sihua1,Zhu Chengjiu2,Jin Xi2,Xu Kangkang2,Yang Bixia3,Yang Shuyi4,Wang Quan4,Tang Wanhe1
(1.School of Mechanical and Energy Engineering,Guangdong Ocean University,Yangjiang,Guangdong 529500,China;2.School of
Electromechanical Engineering,Guangdong University of Technology,Guangzhou 510006,China;3.Guangdong Zhongke Qihang Technology Co.,Ltd.,Foshan,Guangdong 528225,China;4.School of Mechanical Engineering,Hubei University of Technology,Wuhan 430068,China)
Abstract:Isogeometric analysis(IGA)has received widespread attention as a new numerical analysis method.Traditional NURBS curve modeling in geometric analysis suffers from problems,such as a large number of control points,weak local refinement,and poor model space continuity caused by multi-patch stitching.To address these issues,a PHT spline hierarchical subdivision-based IGA method is proposed and applied to study wind turbine blades.Taking a certain wind turbine blade as the research object,the influence of PHT spline refinement on the accuracy of wind turbine blade model solutions is analyzed,and the results are compared with finite element simulation results.The research results show that the relative error between the IGA result based on the NURBS wind turbine blade model before refinement and the finite element result is 5.9%;after PHT spline refinement,the relative error between the IGA result and the finite element result is reduced to 3.7%,which effectively improving the IGA solution′s accuracy for wind turbine blades.The proposed method has important guiding significance for future wind turbine blades′numerical simulation and optimization design.
Key words:wind turbine blade;PHT spline;isogeometric analysis;non-uniform rational B-spline
0引言
非均匀有理B样条(Non-Uniform Rational B-Spline NURBS)是等几何分析的基础,是计算机辅助设计(CAD)中应用最为广泛和成熟的技术,其在CAD系统中的作用是不可替代的。随着等几何分析方法的不断发展,NURBS建模存在如下问题:(1)NURBS在建模过程中会存在多余的控制点;(2)NURBS在局部细化方面能力不足;(3)对于复杂的模型NURBS建模存在多面片拼接的情况,需要对其进行裁剪,会影响模型的空间完整性。为了克服上述缺点并为建模提供更大的灵活性,Deng[1]首次提出了PHT样条的定义,它作为B样条的推广,将张量积形式得以保留,使局部细分变得简单。PHT样条是国内外的研究热点。贾悦[2]提出一种基于改进的PHT样条单元的自适应等几何配点法。该算法结合PHT样条单元的特点,选取高斯点作为配置点。实例计算结果表明,基于改进的PHT样条的自适应等几何配点法可以扩展至任意高阶单元计算,并满足最佳收敛率,且与理论值吻合。Nguyen[3]提出了一种在分层T网格上使用多项式样条(PHT样条)对薄壳进行等几何分析的新方法,该方法利用T网格的灵活性进行局部细化,可以实现模型的C1连续性,并通过数值结果验证了该方法的优越性。Nguyen[4]提出了一种基于多项式样条的自适应扩展IGA方法,其目的是解决等几何分析中的自适应局部细化问题,并将其应用于裂纹扩展的仿真模拟。所提方法克服了基于非均匀有理B样条的限制,使得模型的局部细分具备更大的灵活性。Qarariyah[5]研究了PHT样条的自适应方法以解决奇点问题,通过示例验证了该方法的正确性和优越性。Herrema[6]利用等几何分析创建了一个优化设计的框架,它采用IGA方法,同时严格遵循设计参数化,然后分析模型的有效性和交互性,以压管和风力机叶片为例,证实了该框架的实用性。Josef Kiendl[7]提出了一种克服传统有限元分析(FEA)缺点的等几何分析(IGA)仿真方法,讨论了在风力机叶片设计中IGA特有的问题,同时也提出了一种气动性分析与遗传算法相结合的设计方法。Deng[8]在Rhino中建立了一个集结构建模、分析和参数优化于一体的风力机叶片数值模拟框架。该框架以NREL 5-MW叶片为模型,优化后的叶片气动性能提高了20.9%。Johnson[9]将等几何分析方法应用到风力机叶片的积冰分析中,将复杂的冰结构叠加到叶片的结构上,对不同的冰结构进行叶片的线性振动和非线性偏转分析,以证明不同的积冰分布对结构性能的影响。Van[10]针对传统风力机叶片流固耦合分析成本较高问题,将等几何分析方法引入到风力机叶片的流固耦合分析中,发现等几何分析可以产生高阶自由度加快数据传递过程,降低了流固耦合的计算成本。Stein[11]提出了一种基于等几何分析对物体建模和存储的新方法,然后用该方法构造了适合流体-固体相互作用分析的风力发电机模型。Johnson[12]将等几何分析方法用于分析风力机叶片在积冰下的动力学特性,发现叶片积冰会降低其固有频率和转速。Ferede[13]提出了基于等几何分析的基本框架,用于风力机叶片的气弹耦合分析。Zhong[14]基于精细板理论(RPT)和等几何方法(IGA)提出了一种在热环境下对可变厚度叶片进行超音速颤振分析的建模程序,并通过相关数据验证了所建模型的准确性和稳定性。此外Otoguro[15]将等几何分析方法引入垂直轴风电机组的计算流体分析中,并验证其有效性。
综上所述,国内外学者对等几何分析进行了大量的研究,但以上研究大多基于简单模型的等几何分析,风力机叶片作为一种高级复杂的曲面,在PHT样条分层细化方面的研究还很少。为了实现复杂三维风力机叶片设计与分析的统一,避免复杂的网格划分过程,提高等几何分析的求解精度。本文对风力机叶片PHT样条细化展开研究,以解决风力机叶片NURBS建模及分析存在的问题,为后续风力机叶片的优化设计打下基础。
1风力机叶片等几何分析模型的构建
在风力机叶片设计和分析过程中,设计者通常会先设计其CAD模型,然后通过有限元分析软件对其进行网格划分,此时网格划分的质量也就决定了仿真分析的精度与效率,特别对于风力机叶片这种复杂的曲面,容易划分低质量的网格,影响分析结果的精度与效率。为此本文基于NURBS构建适合等几何分析的风力机叶片二维三维模型,模型设计和分析都采用同一基函数,不仅避免了复杂的网格划分过程,同时也消除了模型设计与分析之间的误差。
1.1叶片翼型NURBS曲线的构建
等几何分析是将产品设计和分析都采用同一函数表达,将NURBS作为设计和分析基函数,连接了设计和分析的桥梁。一条p次NURBS曲线定义为:
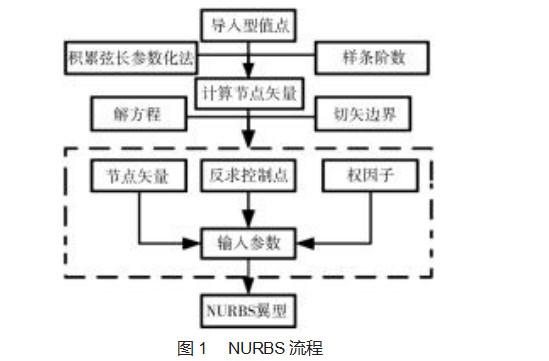
在MATLAB中,先编写翼型反求控制点程序,得到二维翼型的控制点,然后基于NURBS理论编写构建翼型程序,其流程如图1所示。
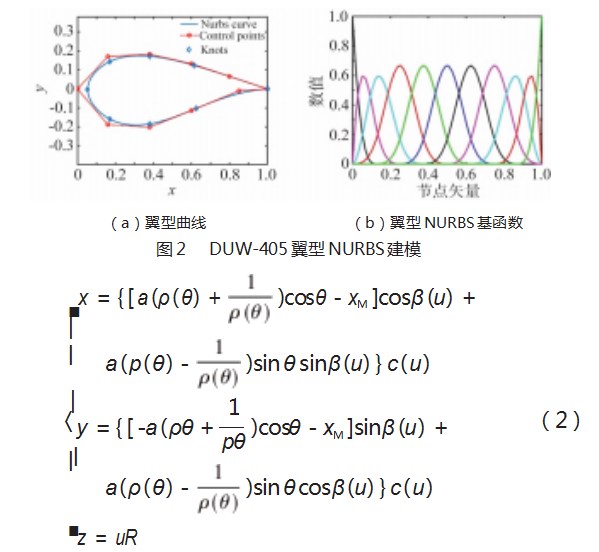
首先选择翼型的型值点,然后通过积累弦长参数化法进行参数化处理,并确定样条的阶数,求得节点矢量信息,再通过切矢边界条件(控制点的首末端点和型值点的首末端点重合),求解线性方程组A×D=E,获得控制顶点向量D,接着将得到的控制点和节点矢量及权因子作为输入参数,得到NURBS构建的翼型。如图2展示了原始翼型为DUW-405翼型的NURBS模型,选取了部分的型值点,求得其控制点信息为:
叶片是以气动中心轴进行扭转的,翼型的气动中心为1/4弦长位置,一般变弦长变扭角的三维叶片集成表达式[16]为:
式中:ρ(θ)为翼型分布函数;xM为翼型气动中心展向位置,一般取0.25;c(u)为弦长分布函数;β(u)为扭角分布函数。
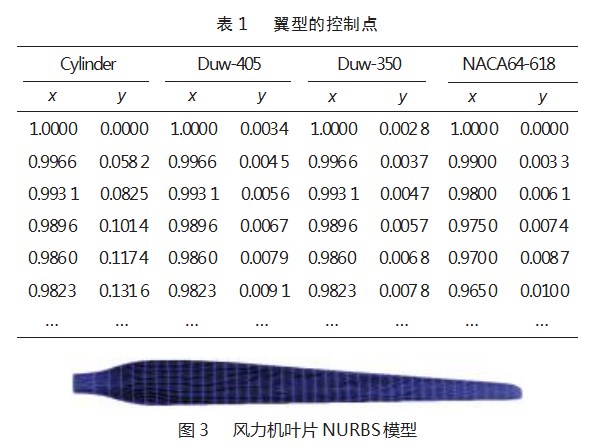
根据三维叶片的形函数/分布函数公式将其耦合到NURBS建模中。分别设置21个翼型的数据,每个翼型由24个控制点构成,其中12个控制上翼型,12个控制下翼型,部分翼型的控制点坐标如表1所示,图3所示为基于NURBS构建的三维风力机叶片模型。
2风力机叶片的PHT样条细化
2.1叶片PHT样条细分思想
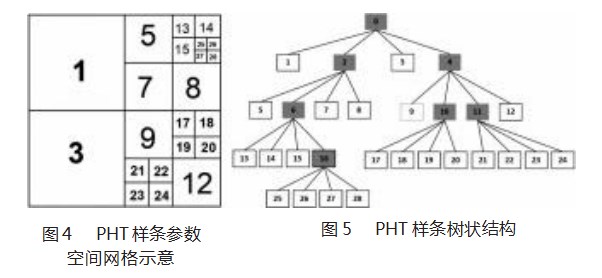
H.Samet[17]提出了四叉树和八叉树的树状结构其及对样条空间进行分层细化的概念,图4所示为PHT样条参数空间网格示意,其可以清楚地表示PHT样条细化在参数空间网格中的细分情况。图5所示为四叉树的概念,树的每一个节点或叶都保存着元素在参数空间的坐标位置及其基函数的坐标信息,相邻单元之间通过指针组合连接。在图4中,单元0是单元1、2、3、4的父单元,其中单元2和单元4为细分单元,也称为树节点,单元1和单元3为树叶不再细分,其中单元6由子单元5、6、7、8继承,通过树状结构图可以很好的表示各个细分单元之间的关系。
根据图5,需要在初始的粗糙网格上定义PHT的样条结构几何单元,首先定义网格的维度为:(p+1)(q+1),然后从u、v两个方向定义节点分布的个数,定义结构体的伪代码如下,其中有输入p、q的阶数,和U、V单元的个数;c为Bezier提取算子,PHTelem为结构体,PHTelem.neighbor_left为单元附近相连接的左单元,PHTelem.neighbor_right为单元附近相连接的右单元,PHTelem.neighbor_down为单元附近相连接的下单元,PHTelem.neighbor_up为单元附近相连接的上单元,其中PHTelem.parent为单元中的父单元,PHTelem.children为单元中的子单元。
2.2叶片PHT样条细化流程
给定风力机叶片计算域Ω∈Rd,表达式为:
2.3叶片等几何分析PHT样条细化模型
针对NURBS建模存在的问题,PHT样条可以去除多余的控制点,具有较强的局部细化能力。为此,对风力机叶片模型进行等几何分析细化研究。对比分析细化前后对风力机叶片等几何分析求解精度的影响,输入参数:octupleRef(存储数据),octupleList(存储矩阵编号),PHTelem(PHT样条结构体),p,q,r,dimBasis(样条空间的维数)输出参数:octupleList(存储有且仅有最小子单元的编号矩阵),PHTelem,dimBasis,其部分代码如下,得到细分后的模型如图7所示。
可知叶片从叶根到叶尖位置的弦长与扭角逐渐减小。与叶片PHT样条细分前模型相比,细分后的叶片模型其控制点数目有所增加,且叶片的翼段被PHT样条细分成多个翼段,实现了风力机叶片的局部细分,解决了叶片在NURBS等几何分析中局部细分能力不足的问题。
2.4叶片等几何分析相关参数设置
根据风力机叶片PHT样条求解流程图,设置材料信息,设弹性模量为1×105 MPa,泊松比为0.3,密度为7.8×103 kg/m3。定义弹性矩阵为:
式中:C为弹性矩阵;b为体积力;ε为应变。
利用伽辽金方法通过选取基函数将其叠加,将计算结果在求解区域内加权积分,可得到求解的线性方程。
对于等几何分析,常见的边界条件主要有狄利克雷边界条件,其直接规定了位移在边界上的数值也叫本质边界条件;诺依曼边界条件规定了在边界外法向方向导数的数值,也叫自然边界条件;还有罗宾边界条件,其为狄利克雷和诺依曼边界条件的组合。本文考虑风力机叶片线弹性静力学问题,故只讨论狄利克雷边界条件。约束情况如图8所示。为方便计算,考虑在叶片挥舞方向受载这一工况下的三维风力机叶片的等几何分析,根据挥舞方向实际受载情况,其具体约束设置为每个节点的Y、Z方向固定,X方向受位移约束-1 mm,将风力机叶片的叶根位置固定。
3结果与讨论
3.1 PHT样条细分程序验证
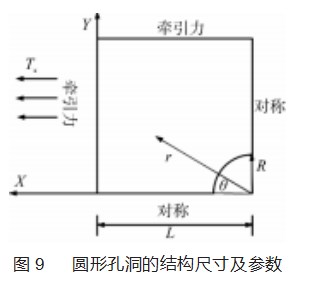
为了验证PHT样条细分算例的正确性,本文考虑一个圆形孔洞的常见算例,由于该模型的对称性,只考虑对其1/4部分进行建模,主要由2个PHT面片组成,其结构尺寸及相关参数如图9所示。模型在x方向受载Tx=10,R=1,L=4,板的材料属性为弹性模量E=105,泊松比ν=0.3,根据相关理论知识,该算例模型的精确解表达为[18]:
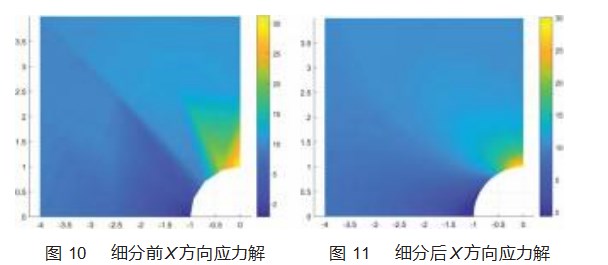
细分前后X方向应力解分别如图10~11所示。由图可知,细分前与精确解的相对误差为4.63%,经过PHT样条细分后,模型与精确解的相对误差为0.48%。从而说明圆形孔洞模型基于PHT样条的求解结果与精确解相差无几。通过此算例验证了PHT样条细分程序和PHT样条等几何分析程序的正确性。
3.2叶片PHT样条细分前后结果对比
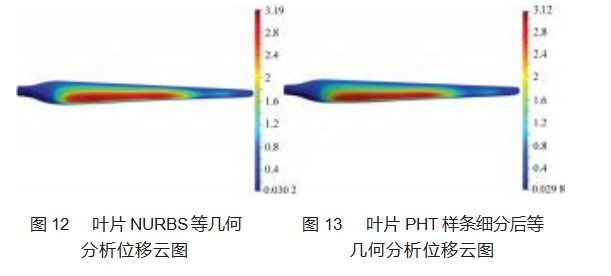
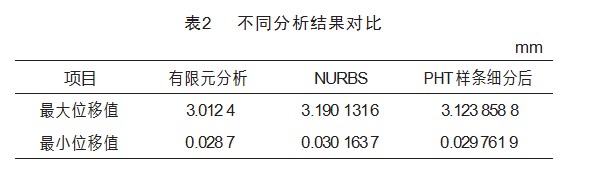
为了将叶片等几何分析结果可视化,本文将求解结果输出为.vtu文件格式。然后,将风力机叶片等几何分析结果导入开源软件Paraview中进行可视化,得到了如图12和图13所示的叶片等几何分析细分前后的位移云图。基于NURBS的叶片等几何分析最大位移为3.190 131 6 mm,最小位移值为0.030 163 7 mm;叶片经过PHT样条细分后,其最大位移为3.123 858 8 mm,最小位移数为0.029 761 9 mm。
在不断细分风力机叶片的过程中,由于叶片模型缺乏解析解,为了有效评估细分前后的误差,考虑用有限元分析软件的计算结果作为参考基准,对比分析PHT样条细分前后与有限元结果的相对误差。不同分析结果对比如表2所示。由表可知,PHT样条细分前与有限元分析结果的相对误差为5.9%;在PHT样条细分后等几何分析的结果与有限元分析结果的相对误差为3.7%。由此可见,经过PHT样条细分后,风力机叶片的等几何分析计算精度得到了一定提高。
4结束语
鉴于风力机叶片等几何分析过程中,如果采用NURBS样条细分网格,会存在控制点较多、局部细化薄弱及多面拼接等问题。本文利用PHT技术对风力机叶片等几何分析进行了样条分层与细化研究,编撰了风力机叶片PHT样条分层细化的相关程序,并与有限元计算结果进行了对比分析。结果表明:基于NURBS的风力机叶片等几何分析结果与有限元计算结果的相对误差为5.9%;而基于PHT样条分层与细化技术的风力机叶片等几何分析结果与有限元计算结果的相对误差为3.7%。证明了风力机叶片经过PHT样条细分后其等几何分析求解精度得到了有效提高。
参考文献:
[1]DENG J S,CHEN F L,LI X,et al.Polynomial splines over hier⁃archical T-meshes[J].Graphical Models,2008,70(4):76-86.
[2]贾悦,ANITESCU Cosmin,李春.基于改进的PHT-样条自适应等几何配点法[J].图学学报,2022,43(1):110-117.
[3]NGUYEN-THANH N,KIENDL J,NGUYEN-XUAN H,et al.Rotation free isogeometric thin shell analysis using PHT-splines[J].Computer Methods in Applied Mechanics and Engineering,2011,200(47/48):3410-3424.
[4]NGUYEN-THANH N,ZHOU K.Extended isogeometric analysis based on PHT-splines for crack propagation near inclusions[J].International Journal for Numerical Methods in Engineering,2017,112(12):1777-1800.
[5]QARARIYAH A,DENG F,YANG T H,et al.Isogeometric analy⁃sis on implicit domains using weighted extended PHT-splines[J].Journal of Computational and Applied Mathematics,2019,350:353-371.
[6]HERREMA A J,WIESE N M,DARLING C N,et al.A frame⁃work for parametric design optimization using isogeometric analy⁃sis[J].Computer Methods in Applied Mechanics and Engineer⁃ing,2017,316:944-965.
[7]HERREMA A J,KIENDL J,HSU M C.A framework for isogeo⁃metric-analysis-based optimization of wind turbine blade struc⁃tures[J].Wind Energy,2019,22(2):153-170.
[8]DENG X W,WU N,YANG K,et al.Integrated design framework of next-generation 85-m wind turbine blade:modelling,aero⁃elasticity and optimization[J].Composites Part B:Engineering,2019,159:53-61.
[9]JOHNSON E L,HSU M C.Isogeometric analysis of ice accretion on wind turbine blades[J].Computational Mechanics,2020,66(2):311-322.
[10]VAN OPSTAL T,FONN E,HOLDAHL R,et al.Isogeometric methods for CFD and FSI-simulation of flow around turbine blades[J].Energy Procedia,2015,80:442-449.
[11]STEIN P,HSU M C,BAZILEVS Y,et al.Operator-and tem⁃plate-based modeling of solid geometry for Isogeometric Analy⁃sis with application to Vertical Axis Wind Turbine simulation[J].Computer Methods in Applied Mechanics and Engineering,2012,213/214/215/216:71-83.
[12]JOHNSON E L,HSU M C.Isogeometric analysis of ice accre⁃tion on wind turbine blades[J].Computational Mechanics,2020,66(2):311-322.
[13]FEREDE E,ABDALLA M M,VAN BUSSEL G J W.Isogeomet⁃ric based framework for aeroelastic wind turbine blade analysis[J].Wind Energy,2017,20(2):193-210.
[14]ZHONG S F,JIN G Y,YE T G,et al.Supersonic flutter analysis of variable thickness blades in thermal environment by using isogeometric approach[J].Thin-Walled Structures,2022,172:108844.
[15]OTOGURO Y,MOCHIZUKI H,TAKIZAWA K,et al.Space–Time Variational Multiscale Isogeometric Analysis of a tsuna⁃mi-shelter vertical-axis wind turbine[J].Computational Me⁃chanics,2020,66(6):1443-1460.
[16]陈进,汪泉.风力机翼型及叶片优化设计理论[M].北京:科学出版社,2013.
[17]SAMET H.Foundations of multidimensional and metric data structures[M].Amsterdam:Elsevier/Morgan Kaufmann,2006.
[18]GOULD P L.Introduction to Linear Elasticity[M].New York,NY:Springer New York,1994.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/77255.html