SCI论文(www.lunwensci.com)
摘要:现有力控打磨系统多采用基于PLC(Programmable Logic Controller)控制气动泵的结构,存在反应慢、精度低等问题。提出了一款基于MCU(Micro Processor Unit)带动丝杆控制弹簧结构的恒力控制系统,能够将气动系统的力控精度由2~10 N提高到0.2~0.5 N量级,反应时间由1~3 s提高到几十ms。首先对丝杆控制弹簧的机械结构进行数学建模,给出了系统响应时间随着电机转速与扭矩、丝杆比、弹簧倔强系数、斜坡角度等物理量的变化的闭式解,随后从模型中分析了提出的系统结构将反应时间降低为几十ms所需的条件以及将力控精度达到零点几牛的关键因素。为了实现上述性能,提出了一种基于弹力补充原理的恒力控制方案,仿真和实验发现该方案比传统PID(Proportional Integeal Differential)的控制方案更接近理论上的响应速度以及力控精度,可广泛应用于工业打磨和抛光,实现更精细的打磨要求。
关键词:恒力控制系统;力控精度;反应时间;弹力补充
A Constant Force Control System Based on MCU Electromechanical Elasticity
Supplement Principle
Wu Minmin,Liu Sanjun
(School of Intelligent Science and Engineering,Hubei University for Nationalities,Enshi,Hubei 445000,China)
Abstract:The existing force control polishing systems mostly use a structure based on PLC(Programmable Logic Controller)to control pneumatic pumps,which has problems such as large volume,high price,slow response,and low accuracy.This article proposes a constant force control system based on MCU(Micro Processor Unit)driving screw control spring structure,which can improve the force control accuracy of the pneumatic system from 2~10 N to 0.2~0.5 N,The reaction time has increased from 1~3 s to several tens of milliseconds.A mathematical model of the mechanical structure of the screw control spring is first established,providing a closed form solution of the system response time as a function of physical variables such as motor speed and torque,screw ratio,spring stubbornness coefficient,slope angle,etc.Subsequently,the conditions required for the proposed system structure to reduce the response time to tens of milliseconds and the key factors for achieving force control accuracy to a few tenths of Newton are analyzed from the model.In order to achieve the above performance,a constant force control scheme based on the principle of elastic compensation is proposed.Simulation and testing founds that the scheme is closer to the theoretical response speed and force control accuracy than the traditional proportional integral differential(PID)control scheme,and can be widely used in industrial polishing and polishing to achieve more precise polishing requirements.
Key words:constant force control system;force control accuracy;response time;elastic compensation
0引言
打磨抛光是制造业最常见的工序之一[1],主要有人工打磨和工业机器人打磨两种,人工打磨抛光存在打磨粉尘大、人工成本高和品控不稳定等问题[2-4]。相比之下,工业机器人打磨具有效率高、品控稳定等优点,因此使用工业机器人进行自动打磨已经成为制造业的切实需求[5-7]。工业机器人在打磨抛光时,需要精确控制工具头与工件间的接触力。在实现对接触力的控制方面,目前存在两种主要方法[8]。一种方法是直接控制机器人的关节力矩实现力的控制,通过在关节上施加适当的力矩控制机器人在执行任务时的力度,这种方法涵盖了位置控制、速度控制和力矩控制等控制方式,但这种方法对机器人动力学要求较高,会增加机器人控制程序的复杂度,从而限制了系统的鲁棒性和稳定性[9]。为了克服这些局限性,研究者们转向另一种方法,即在机器臂与工具头之间安装力控机构实现进行力的控制,具体来说,通过在机器人末端安装力传感器和执行器实时监测接触力,并根据设定的力来控制接触力的大小,这种方法可以实现对接触力的精确控制,使得机器人在与环境或对象进行交互时更加灵活和智能化[10-11],这种方法虽然需要增加一个专业的力控机构装置,但是能够显著的提高力控精度、反应时间,并降低机器人的复杂度。
现有力控机构装置从硬件结构上主要分为气动、电动结构,气动结构往往存在力控精度低、稳定性较低等问题,普遍的力控精度为1~2 N,反应时间为数秒;电动结构相较于气动结构具有更高的精度和稳定性,但会面临惯性和摩擦力的问题,需要控制算法和反馈系统来实现力控制性能。比如何邦[12]设计了一种可以安装在机器人末端的气动恒力控制装置,该装置仅能提供竖直方向的恒力输出,并且在作业环境发生变化时会对控制装置产生损害。何伟崇[13]提出了一种面向工业机器人打磨抛光的一维装置,但存在装置与工件接触瞬间,输出力无法快速响应的问题。为了提高恒力控制系统的性能,一些研究者提出了更先进的力控结构,例如,Abd El Khalick Mohammad等[14-15]提出了一种力控结构,采用线性空心音圈致动器扩展和缩回来减少惯性效应,该结构集成了力传感器,实时测量抛光力并反馈给控制器,但由于惯性的存在使得精度不高。此外,张林等[16]提出一种新型三自由度力控打磨系统,其主要由电主轴、抛光头、力传感器、动平台、定平台等组成,并将各个元件集成结构紧凑的力控打磨系统,通过3个音圈电机驱动,适用于工件狭小空间处的自动化打磨抛光,但设计过于复杂。为此本文提出了一种利用MCU控制丝杆推动弹簧伸缩量从而实现恒力控制的机械装置,MCU充当控制中枢,通过力传感器检测和分析实时力的信息,再通过电机调整丝杆的推动速度与距离,进而控制弹簧的伸缩对所需的力施加精确的控制。相较于气动结构,由于弹簧和丝杆等装置的机械特性相对稳定,该装置能够适应不同的工作条件,并且结构简单,力控精度高、反应迅速、能适应更多的应用场合。
要想让这些机械装置实现实时的恒力控制,需要综合考虑力的实时测量、运动部件的迅速响应等多方面因素,统筹这些因素的常见方法一般是采用PID控制器通过实际打磨力与目标力之间的差异来实现对机械装置的力控制,为了进一步改进PID控制的性能,研究者们持续不断地进行探索和创新,以提升其控制性能。比如吴安根[17]对传统PID控制、积分型线性自抗扰控制(I-LADRC)、线性PID自抗扰控制3种控制算法进行分析,传统PID在跃变较大的输入信号,无法解决快速性和超调之间的矛盾;I-LADRC在期望信号突变时,存在一定的超调和抖振问题;线性PID自抗扰控制要考虑的参数太多,设计的控制器太复杂;分线性PID自抗扰控制具有更高的力控制精度、更好的动态响应以及更强的鲁棒性,但控制方法较为复杂,并且在实际打磨中系统稳态误差只能达到2 N左右。曾顺麟[18]使用了改进粒子群算法优化的模糊PID控制进行控制,整个系统的超调量下降,收敛时间降低,但是力控环节对外界工作环境的变化不够敏感,系统的精度较低。
本文测试了基于PID控制方案的恒力控制系统的精度和反应时间,并发现其力控精度可以达到0.2~0.5 N,但反应时间难以达到毫秒级,且系统存在弹簧多次微调的情况,导致不稳定的振动,从而降低了系统的整体性能水平。为此,本文提出了一种弹力补充的控制方案,以期进一步提升系统的力控制性能和稳定性。当实际打磨力通过工具头作用于力控机构的装置时,弹簧会变形将能量存储在其中,随后释放储存的能量,通过MCU计算缺失的反作用力的大小,然后控制电机带动丝杆运动,使得反作用力得到补充,补充后的反作用力能够正好弥补所缺失的推力或者抬升力,从而达到恒力控制。结果表明使用本文的控制方案单位力控精度可达到小于或等于0.2 N,反应时间在100 ms以内。
1系统结构
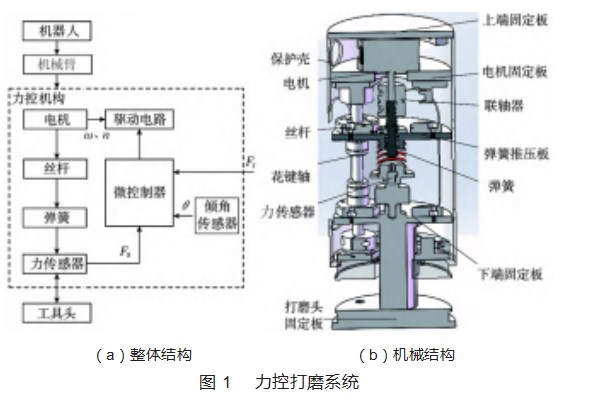
恒力控制系统一般由机器人的机械臂控制力控机构的整体运动轨迹,如果被打磨物体表面没有凸起或者凹陷,则力控机构头部的伸缩量是恒定的,打磨的压力也是恒定的,当物体表面存在凸起或者凹陷时,会带动力控头部产生不同的伸缩,导致打磨力发生变化,这时,系统中力传感器会感受到这个力的变化情况,MCU控制丝杆产生运动带动头部产生反方向的伸缩,从而达到恒力打磨的目的。力控打磨系统的总体结构如图1(a)所示,主要由机器人、电机、丝杆、弹簧、力传感器、倾角传感器、微控制器(MCU)等组成。上述部件安装在一个密闭圆柱形的外壳内,用于防止打磨环境中的尘埃对装置的影响,如图1(b)所示。电机通过联轴器与丝杆相连,通过联轴器将电机的扭矩传递给丝杆,通过电机的正反转带动丝杆连接的弹簧伸缩,让最下端的工具头对打磨物体表面的打磨力发生变化,力的大小Fa可由弹簧与工具头之间的力传感器精确地测量出来。
系统的工作过程分为两步,第一步是自动校准初始力的过程,用来保证系统刚开始工作(静止于物体表面)的时候对物体表面的压力等于设定值Fr。这个过程需要平衡工具头的重力,设工具头质量为m,重力加速度为g,则工具头的重力为mg,通过倾角传感器测量力控装置的中轴与竖直方向的夹角θ(0°≤θ<180°),则MCU控制弹簧产生合适的长度使得弹簧对工具头产生的推拉力大小为:
Fa=Fr-mg cosθ(1)
这个力的大小可由力传感器测量出来,系统使用的力传感器是推拉力传感器,式(1)计算出的Fa可能为正也可能为负,当Fa为正时,表示MCU需要控制弹簧压缩使得弹簧对工具头施加推力;当Fa为负时,则表示MCU需要控制弹簧拉伸使得弹簧对工具头施加拉力,系统通过丝杆调节弹簧伸缩量的方式调节Fa的大小,使得力传感器检测出来的Fa等于式(1)推算出来的大小,从而使得系统起始工作的时候给物体表面施加的力等于设定的Fr。
随后,系统进入第二步,即恒力打磨过程,机械臂带动力控机构沿着物体表面发生平移运动,假设行进速度为v,微控制器通过力传感器不断测量打磨时工具头与工件间的打磨力Fa,并与预期值Fr进行比较,依据二者之间的差异调节电机的转动使得Fa不断接近Fr的大小,从而实现恒力打磨的过程。在这个过程中电机的转速ω以及旋转的圈数n应该如何又快又准的进行控制,成为本文研究的重点,本文提出了一种全新的基于弹力补充的恒力控制方案,相较于传统的PID控制方案具有诸多优势。由于ω和n显然会受到v以及打磨面的凹凸曲率的影响,本文首先从理论上研究它们之间的制约关系,随后再讲解如何实现最佳的控制以满足这些条件。
2系统建模与求解
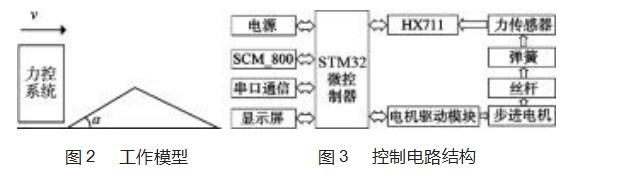
由于系统实现的效果是能够在粗糙的打磨面上尽可能迅速的恒力控制,被打磨面的倾角α越大、机械臂的运动速度v越快则对控制的反应速度、丝杆的伸缩速度的影响越大,因此,本文首先从理论上分析丝杆伸缩速度、电机需要的最高转速、系统响应速度等物理量与打磨面的倾角α以及机械臂的运动速度v之间的关系,给出他们之间的制约方程。根据系统需求,在不考虑机器臂适应工作面而动作的情况下,建立系统的工作模型图,如图2所示,系统从检测力的变化到电机在下一个检测前进行动作的时间记为执行周期t,斜面上存在数个执行周期。
当系统从斜面底部开始运动,经过τ(τ<t)的时间,τ为执行周期中力传感器检测到打磨力发生变化以及MCU经过运算后得出电机所需圈数与转速的时间,此时水平运动的距离为vτ,斜面角度为α,那么斜面使得工具头抬起的距离为:
h=vτ·tanα(2)
式(2)中,h也可以看成是弹簧的形变量,在某时刻后,MCU感应到打磨力发生变化,并让电机、丝杆部分在t-τ的时间内作出反应,使得电机带动丝杆运动,改变弹簧的形变量,使得打磨力向预期打磨力允许的误差范围内靠近。此时,在弹簧倔强系数k确定的情况下,弹簧所需产生的弹力Fs为:
Fs=kh(3)
那么电机需要带动丝杆移动h的距离,故可得电机所需转速应ω满足:
式中:r为丝杆的半径;s为丝杆的导程,即电机带动丝杆转一圈所移动的长度,只要电机的转速满足式(4)这个条件系统就能在t-τ的时间内反应过来。
以电机的最低转速推算圈数,那么在t-τ的时间内,电机所需圈数n为:
n=2πω(t-τ)(5)
根据算出的转速和圈数,电机将以ω的转速转动n圈,使得丝杆弹簧补偿FS斜面对打磨系统的力,在任意执行周期中,存在τ与t的关系为:
tp≥τ/t(6)
在执行周期t确定的理想情况下,当tp较大时,即检测力变化以及程序运行的时间较长,那么电机控制丝杆改变弹簧伸缩量的动作时间t-τ就会减少,但过短的动作时间就要求电机需要极高的转速才能执行完MCU指定的操作进入下一个执行周期,电机转速过快会导致电机发热、使用寿命降低等情况。当tp较小时,即检测力变化以及程序运行的时间较短,那么电机控制丝杆改变弹簧伸缩量的动作时间会增加,会影响实际打磨的效率。
3系统的软硬件设计
现有的恒力控制系统在打磨过程中,当预设打磨力为20 N,输出力会出现±2 N范围的波动,一但出现超过±2 N的波动就需要数秒钟的时间才能调整过来[19]。而要使本系统的单位力控精度达到0.2 N,反应时间为几十ms,在已经确定机械部分的情况下,需要选择合适的硬件适配机械部分,同时对软件程序进行设计达到本文所需的控制条件。
3.1硬件设计
为了保证电路硬件要求能在复杂的现场环境也能稳定工作,系统硬件部分选择了包括STM32微控制器、力传感器、倾角传感器、电源、电机驱动模块等设备。控制电路结构如图3所示。
微控制器选取STM32,其价格便宜、性能优秀,可以支持复杂的应用拓展,并且具有良好的稳定性和可靠性,在控制领域中占据重要地位。力传感器选取微型的HYLY-019压力传感器,体积小、精度高、性能稳定,可以达到0.05 N的精度,力传感器需使用A/D模块HX711进行运算放大并检测压力,再传输至STM32。倾角传感器选取SCMA_800,小体积、低功耗、高稳定、低成本,测量精度可达0.8°。电源模块采用12 V的直流电源作为输入电源,通过AM1117-5和AM1117-3.3两款压降稳压器设计的电源电路可得到5 V和3.3 V的电压,为电路中各模块供电。电机驱动模块中使用A4988驱动器驱动步进电机,其价格便宜,操作容易。步进电机型号为39HS2606A4,其步距角为1.8°,静力矩为8 N·cm,定位力矩0.5 N·cm,转动惯量为12 g·cm2,极对数为50。显示屏上会显示当前系统中轴与竖直方向的倾角以及实际打磨力。
3.2软件设计
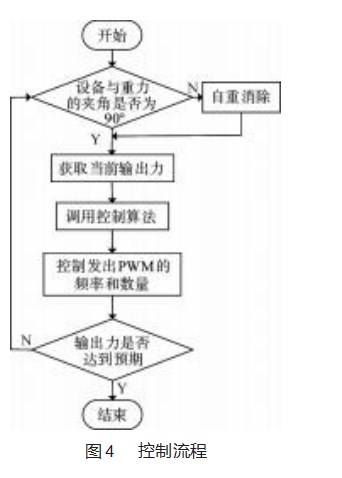
当机器人按预定轨迹达到打磨起始定位点后,会向力控机构发送一个准备完成的信号,然后等待系统开始工作,系统的控制流程如图4所示。在系统的控制流程中,首先根据倾角传感器测量打磨系统中轴线与重力方向的夹角,并结合力传感器的数据消除重力对打磨的影响。然后计算实际打磨力与预期打磨力的偏差,并将偏差代入控制算法,调整实际打磨力。直到力传感器传递给MCU的实际打磨力,满足预期打磨力与实际打磨力误差的要求。这样的控制流程能够保证在机器人进行打磨操作时,实现准确的打磨力控制,从而达到预期的打磨效果。
本文的算法具体流程如下:输入预期打磨力Fr,实际打磨力与期望打磨力的最大允许误差Fmax,获取实际打磨力Fa;通过Fa-Fr=Δf计算得到实际打磨力与预期打磨力的偏差Δf;若|Δf|≤Fmax,保持当前打磨力不变;若|Δf|>Fmax,再根据Δf的正负情况调整打磨力的方向;计算出脉冲的数量与频率调整的打磨力,并将其应用于打磨操作。
通过以上算法流程,可实时计算实际打磨力与预期打磨力的偏差从而调整打磨力的大小,直至偏差达到允许的误差范围Fmax内。脉冲的数量与打磨力的大小有关,这样的算法流程能够有效地控制打磨力,并保证打磨的精度和稳定。根据算法流程,可得所需脉冲的个数i为:
式中,q为电机一个脉冲旋转的角度,本系统中的电机步距角为1.8°,那么电机转一圈所需脉冲n=200个。此外,脉冲频率的大小与系统反应时间有关,即系统调整实际打磨力与预期打磨力的偏差所用的时间,为了不增加算法的复杂度,本文通过实际打磨力与预期打磨力的绝对值|Δf|以及实际打磨力与期望打磨力的最大允许误差Fmax速度来规定电机转速,其状态逻辑如表1所示。
表1中速度状态的关系为ω1<ω2<ω3<ω4<ω5,在τ时间后,MCU中根据表1中的条件判断出电机的转速为多少,从而计算出电机所需脉冲的频率e,公式如下。
式中:p为电机的极对数;x为1,2,3,4,5中任意一个数。
本系统中电机的极对数为50,若电机转速为10 rad/s,则所需脉冲频率e=800 Hz左右。
4方案对比分析
为了验证本文方法对本文中基于微控制器带动丝杆控制弹簧结构的恒力控制系统及其控制方法有效性,与基于传统PID的控制方案进行比较,在文献[20]中,控制器每隔20 ms的时间获取脉冲数量并判断转向。传统PID控制的实质就是对速度进行分割、切合、取极限,再调用位置式与增量式PID函数实现电机速度与位置的控制,其中位置式与增量式PID控制公式为:
在PID的控制中电机的速度与位置控制都是按式(9)、(10)实现的。文献[19]中算法程序的功能是根据输入的初始位置,并定义一个PID函数。该函数的入口参数为编码器的位置测量值(s)和位置控制的目标值(s1)。程序通过位置式PID控制算法来计算并返回得到一个具体的绝对的数值,表示PWM波形信号。然后该PWM波形信号会被输出给电机驱动函数,以控制电机转动到目标位置。
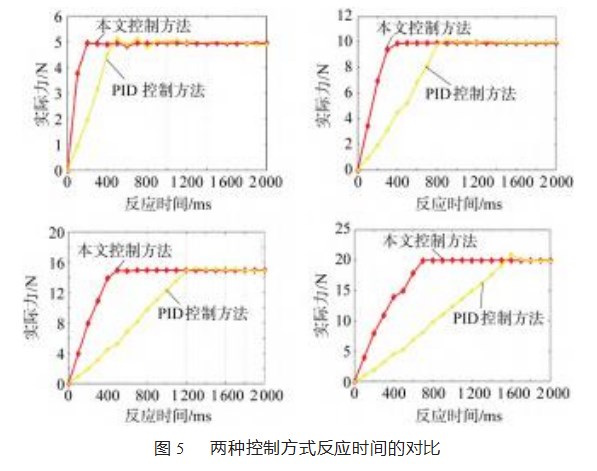
在本文的恒力控制系统中,采用了基于微控制器带动丝杆控制弹簧结构的控制方案,这种控制方案与传统PID控制方案在实现方法和控制策略上有所不同。本文旨在通过比较所使用的控制方法与传统的PID控制方案在恒力控制的精度和响应时间方面的表现,来验证所使用的控制方法的有效性。使用本文设计的恒力控制系统,将预期输出力设置为5 N、10 N、15 N、20 N,误差设置为0.2 N,每次实验开始前都将力传感器测得的值调整为0,依次输入预期输出力,并记录实验数据。在每次实验中,记录预期输出力的值,比较显示的值与预期打磨力之间的差异,评估力的精度,通过串口获取系统的反应时间,并记录下所有的实验数据,最终得到的结果如图5所示。
根据图5中实验结果,在不同预期输出力下,本文的控制方法和传统PID控制方法在力的精度和反应时间方面的比较结果表明,无论采用哪种控制方法,本文的机械结构能够实现力控精度达到0.2 N。这意味着系统可以实现非常准确的力控制,使得在控制过程中所施加的力可以精确地达到目标值,并维持在非常接近的范围内,这种高精度的力控制能够满足对于精细操作和高要求的应用场景。本文提出的控制方法在系统反应时间方面表现出显著的优势,远远超过传统的PID控制方法。相比之下,传统的PID控制方法可能存在较长的响应延迟,导致系统输出在输入变化后需要更长的时间才能达到稳定状态。本文的控制方法通过优化算法、增加控制环节或采用更高效的控制策略等手段,有效减少了系统的响应时间。这使得系统能够更迅速地对输入变化作出反应,实现更快的动态响应和调节能力。在许多应用场景中,系统的快速响应时间至关重要,尤其是在需要实时调节和精细控制的任务中。
因此,基于实验分析,本文系统及其控制方法具有以下优势:在5N的预期力的情况下,平均反应时间缩短了约200 ms,且预期力越大,反应时间的差距越多,本文控制方法的反应时间的标准差也显著较低,表明其具有更稳定的响应性能;在相同的预期力情况下,本文控制方法远优于传统PID控制的反应时间,能够在较短的反应时间内实现所需的力控制精度。需要注意的是,具体的实验结果可能受实验设置、系统参数和环境条件等因素的影响,因此在实际应用中仍需综合考虑这些因素。
5结束语
本文提出了一种基于机电补充原理的恒力控制系统及其控制方法。该系统采用电机、丝杆、弹簧等装置实现机电弹力补充,通过力传感器实时测量打磨头对工件表面施加的力,并在微控制器中使用控制策略来调整打磨头的打磨力,从而显著将打磨精度从数牛顿量级提升到零点几牛顿量级,反应时间从秒量级提升到毫秒量级。本文分析了机械臂的运动速度v、打磨面倾角α对电机转速ω和圈数n的影响,给出了关于ω与n的关系表达式,通过分析发现电机转速与系统反应时间有关,电机圈数与打磨力的大小有关,考虑到成本以及算法复杂度的问题,为此本文采用精确的脉冲个数控制以及与频率大小对应的速度状态控制,实现高精度的力控以及系统的快速反应。
综上所述,本文的恒力控制系统及其控制方法在光滑表面打磨过程中具有明显优势。使用本文设计的力控机构,并采用本文的控制方法的系统能够实现精确控制、快速响应,可在不事先了解系统动态特性的情况下应用于复杂的打磨任务。但系统还是存在内部摩擦力较大和电路接线不规范的问题,目前系统结构和电路仍有改进空间,未来可以通过降低系统内部摩擦力、简化系统结构、规范电路接线等方式,使系统更加可靠和高效,能够满足工业打磨和抛光的应用需求。
参考文献:
[1]李伯民,赵波.现代磨削技术[M].北京:机械工业出版社,2003.
[2]Tian F,Li Z,Lv C,et al.Polishing pressure investigations of ro⁃bot automatic polishing on curved surfaces[J].The International Journal of Advanced Manufacturing Technology,2016,87(1-4):639-646.
[3]王玉珍.打磨作业中加强对振动危害的预防[J].安全知识,2011(10):38-39.
[4]Mohammad A E K,Wang D.Electrochemical mechanical polish⁃ing technology:recent developments and future research and in⁃dustrial needs[J].The International Journal of Advanced Manu⁃facturing Technology,2016:1-16.
[5]徐建明,王于玮,董建伟,等.基于阻抗控制的机器人砂带打磨的建模与仿真[J].浙江工业大学学报,2018,46(2):119-126.
[6]刘志恒.基于力反馈的打磨机器人控制系统研究[D].哈尔滨:哈尔滨工业大学,2017.
[7]米显,库祥臣,马东阳,等.6R关节式机器人奇异性分析[J].机电工程,2022,39(11):1620-1626.
[8]杨桂林.工业机器人运用技术[J].中国科学院院刊,2015,3(6):785-792.
[9]李正义.机器人与环境间力/位置控制技术研究与应用[D].武汉:华中科技大学,2011.
[10]Zhang X,Chen H,Yang N.A structure and control design of constant force polishing end actuator based on polishing robot[C]//IEEE International Conference on Information&Automa⁃tion,New York:IEEE,2017.
[11]刘祚时,吉协福,姜鸿雅.打磨机器人控制系统设计与研究[J].组合机床与自动化加工技术,2020(5):113-115.
[12]何邦.面向工业机器人的气动恒力控制系统的研究[D].青岛:中国石油大学,2019.
[13]何伟崇.面向机器人抛光打磨的一维恒力装置及控制系统[D].广州:广东工业大学,2016.
[14]MOHAMMAD A E K,HONG J,WANG D.Design of a force-controlled end-effector with low-inertia effect for robotic polish⁃ing using macro-mini robot approach[J].Robotics and Comput⁃er-Integrated Manufacturing,2018,49:54-65.
[15]HONG J,MOHAMMAD A E K,WANG D.Improved Design of The End-Effector for Macro-Mini Robotic Polishing Systems[C]//the 3rd International Conference on Mechantronics&Ro⁃botic Engineering,Febrcary 8-12,2017,Paris,France,New York:ACM,2017.
[16]张林,杨桂林,刘立涛,等.一种新型三自由度力控末端执行器及其运动学和性能分析[J].宁波大学学报(理工版),2019,32(1):38-43.
[17]吴安根.机器人打磨的气动恒力控制系统研究[D].福建:福建工程学院,2022.
[18]曾顺麟.基于恒力输出器的打磨系统[D].武汉:湖北工业大学,2021.
[19]黄小娣.面向陶瓷洁具打磨机器人恒力打磨装置系统设计[J].装备制造技术,2020(10):63-65.
[20]赵鹏,钱美,李帅波.单片机PID电机转速与位置控制系统设计[J].工业仪表与自动化装置,2022(4):24-27,44.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/77187.html