基于最优化理论的称重传感系统弹性元体结构优化论文

SCI论文（www.lunwensci.com）　　

　　摘要：弹性敏感元体是测力系统的核心结构，为进一步提高称重传感器敏感性，降低测量误差，首先对圆形、正六角形、正八角形、正十角形、正十二角形5种元件结构进行了力学特性分析，进而确定了以圆环结构为研究对象；其次建立了模型的参数化模型，采用中心复合设计方法生成了28个样本点，并对样本数据进行了多元二次回归拟合，拟合结果表明方程显著性较高，拟合度良好，可以用于预测结构的应变量；最后采用最优化理论结合多目标遗传算法对模型进行优化，经优化共得到3个候选点，经对比选择候选点3做为最优解，此时参数P1=5.117 mm，P2=44.355 mm，P3=19.887 mm，P4=50.047 mm，P5=10.407 mm，结构最大应变差为0.004 845，结构测量敏感度提高了62.80%，测量误差降低了38.56%。研究结果表明，采用优化设计方法，可以显著提高弹性单元体的测量性能。

　　关键词：弹性单元体；有限单元法；中心复合设计；多元二次回归；多目标遗传算法

　　Abstract:The elastic sensitive element is the core structure of the force measuring system.In order to further improve the sensitivity of the weighing sensor and reduce the measurement error,firstly,the mechanical characteristics of five kinds of element structures:circle,regular hexagon,regular octagon,regular decagon and regular dodecagon,are analyzed.And it is determined to take the ring structure as the research object.Secondly,the parameterized model of the model is established,28 sample points are generated by using the central composite design method,and the sample data are fitted by multiple quadratic regression.The fitting results show that the equation has high significance and good fitting degree,which can be used to predict the structural strain.Finally,the model is optimized by using optimization theory and multi-objective genetic algorithm,after optimization,three candidate points are obtained,and candidate point 3 is selected as the optimal solution by comparison.At this time,the parameters P1=5.117 mm,P2=44.355 mm,P3=19.887 mm,P4=50.047 mm,P5=10.407 mm,the maximum strain difference of the structure is 0.004 845,the structure measurement sensitivity is improved by 62.80%,and the measurement error is reduced by 38.56%.The results show that the measurement performance of elastic elements can be improved significantly by using the optimal design method.

　　Key words:elastic element;finite element method;central composite design;multiple quadratic regression;multi-objective genetic algorithm

　　0引言

　　弹性敏感元件的结构设计是国内外的前沿研究课题之一，在测量过程中的敏感性问题一直备受国内外学者瞩目，横梁式弹性敏感元件结构因其结构简单，线性度优良等特点，故而被广泛应用于诸多传感测量领域当中，对弹性敏感元件而言，当受载条件相同，若能够在材料线弹性范围获得更明显的应变差，则有助于提高结构的敏感度，降低测量误差，但根据传统理论设计得到的单元体结构，往往存在安全系数冗余量大、其测量潜能不能充分发挥的问题，同时对于测力系统弹性元件而言，其固有频率与应变值为矛盾关系，其结构优化属于多目标问题，问题求解困难[1-2]。

　　近年来，随着机械领域结构设计研究的逐渐饱和，诸多学者瞩目于机械结构的优化与改进，结构优化设计现已广泛应用于各个工程领域，其基本思路为以结构的设计参数为研究对象，通过调整参数以提高设备的可靠性、稳定性及经济性。赵友等[3]使用正交八角环式弹性敏感元件，对加工过程中的切削力进行实时监测，同时结合理论计算与有限元分析方法，在兼顾结构强度要求的前提下，有效提高了弹性单元体的敏感度和固有频率。龚中良等[4]以横梁式称重传感器弹性单元体为研究对象，以其振动稳定性为优化目标，采用有限单元法及响应面优化方法对单元体进行优化，经优化设计，弹性单元体的二阶固有频率提高了2.47%。赵瑞杰等[5]以正交十角环结构切削测力仪为研究对象针对结构灵敏度与固有频率之间的矛盾问题，采用多目标优化方法，在保证结构震动稳定性的前提下有效提高了结构的灵敏度。王娟等[6]针对三维动态车削测力仪拉压方向灵敏度偏弱的问题，建立模型的刚度、灵敏度综合优化模型对其进行优化设计，最终得到了弹性单元体的理想参数。

　　在国外，Mohammad Uddin等[7]为提高切削测力仪弹性单元体的灵敏度，将其八角形结构改为椭圆形结构，并对其厚度进行优化，经优化后的单元体结构能够在保证结构震动稳定性的前提下，显著提高结构的测量灵敏度。Sheikh-Ahmad等[8]用有限元方法对不同几何尺寸的八角环力传感器中弹性单元体的应力分布和应变分布进行了研究，确定了应变节点的最佳位置和最大灵敏度的位置，找出了贴片最佳位置。

　　综上研究所述，关于提高弹性单元体灵敏度及降低测量误差的问题，可以采用优化设计的方法加以解决。

　　1弹性单元体结构及工作原理

　　1.1弹性单元体结构

　　结合正交八角环切削用测力仪的研究背景[9]，本文以L6N3平行梁式称重传感器结构为基础，设计出了正六角环式、正八角环式、正十角环式、正十二角环及圆环式平行梁式称重测力仪弹性敏感元件。其具体结构如图1所示，图中六边形、八边形、十边形、十二边形均为图1(a)中圆的内接多边形。

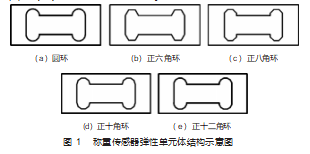
　　1.2称重器工作原理

　　横梁式称重传感器，在工作时结构受载荷作用时单位长度上会产生相应的变形量，其应变量可计算如下：

　　式中：ε为应变量；ΔL为变形量；L为长度。

　　当弹性单元体受载后，其结构会产生应变，此时贴片位置所贴应变片会感知结构的应变量，进而引起应变片电阻值发生相应的变化，并最后通过数据转换系统将应变量转变为数值输出，其测量原理如图2所示。

　　在测量及转换过程中应变式称重传感器会产生两部分误差，在本文中将应变片的横向效应、机械滞后现象等引起的误差总体归类为应变测量误差，将因最大工作电流、温度、湿度和绝缘电阻等引起的误差归类为信号转化误差。

　　一般而言，当结构处于线弹性范围之内时，其在同等载荷下产生的应变量越大，越有助于应变片感知外载荷大小，则弹性单元体结构灵敏度更高，其测量灵敏度可计算为：

　　式中：St为测量灵敏度；F为额定载荷。

　　在系统测量时，其总会存在一定大小的误差，关于应变测量误差百分比可表示为式中：

        Per为误差百分比；εm为测量值；εa为实际值。

　　结合式(3)可知，当测量系统精度保持不变，提高弹性单元体的线性应变量不仅可以提高测量灵敏度，同时也有助于减少应变误差测量百分比。

　　2称重传感器数值模拟

　　2.1有限元模型的建立

　　为保证模型高效准确的迭代以及良好的参数化性能，在下文中结合L6N3平行梁式称重传感器的实际尺寸使用Design modeler模块建立平行梁式称重传感器弹性单元体的三维参数化模型，模型结构如图3所示。

        使用Soild185单元对其进行网格划分，结合网格无关性理论，控制单元格大小为1 mm，其有限元模型在此不做展示。

　　17-4PH因其具有良好的抗拉、抗压、抗腐蚀、抗水滴能力，尤其当经过热处理后其机械性能更加完善，故有一直以来被广泛应用于测力系统核心构件的材料[9]。此次研究选择17-4PH为结构材料，其材料属性如表1所示。

　　2.2有限元数值模拟

　　结合实际工况对弹性单元体施加边界条件，以模拟其在额定载荷下的力学特性，为保证计算结果对比性，控制所有结构网格尺寸大小一致，对上述5种结构在额定工况下的应变值进行计算，其计算结果如表2所示。

　　弹性单元体作为小体积、高精度的机械元件，保证其良好的振动稳定性是其进行精确测量的首要前提条件，系统的动力学方程如式(4)所示[10]

　　式中：M为结构质量矩阵；C为结构阻尼矩阵；K为结构刚度矩阵。

　　其系统的运动学方程如式(5)所示：

　　u=umax e-At sinωt(5)

　　式中：umax最大节点位移；A为系统衰减指数；t为系统运行时间。

　　将上述两式进行联立求解，其前6阶模态频率计算结果如表3所示。由表可知弹性单元体固有频率与其应变差互为反比例关系，与前人研究结论一致，验证了此次仿真的正确性。通过对比表中数据，可知圆形弹性元件在相同的载荷条件下，具备更为明显的最大应变差对于实际工程问题，还应考虑其固有频率对其工作性能带来的影响，称重传感的工作可以近似认为是静态问题，故因结构变化引起的模态频率降低的问题在综合考量时其权重可适当降低。上述5种结构均满足震动稳定性要求，故主要考虑的优化目标为结构的应变差值。

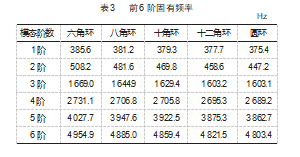
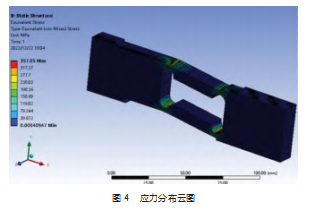
　　结合表2及表3数据可知，圆环形结构在相同的载荷条件下具备更明显的应变量，且其固有频率较其他结构相比水平差距较小，故在下文中选择圆环形结构作为研究对象。经有限元数值模拟，弹性单元体的当量应力分布如图4所示。从图中可以看出，弹性单元体在额定载荷下其最大当量应力为357.05 MPa，其最大应力主要集中在圆环弧顶处，即结构尺寸突变处，同时17-4PH的屈服极限为725 MPa，结合形状改变比能理论可知，即使取折合系数为1.3，弹性单元体仍有较大的安全冗余量，表明结构有足够的优化空间[11]。

　　其结构控制参数示意图如图5所示。弹性单元体内部有4个直径相等的半圆，其分布在如虚线所示的矩形的4个顶点上，其垂直方向依靠两条切线连接，其水平方向从圆弧内侧1/2处以两条平行线连接。图中，P1为圆弧半径，初始值为5 mm；P2、P3为4个圆所分布的矩形的长和高，初始值分别为41.5、18.1 mm；P4、P5为矩形右下方顶点的位置，初始值大小分别为53、9.5 mm。

　　3弹性单元体的结构优化

　　依据传统经验设计方法或理论设计方法得到的结构虽然能够保证弹性单元体工作的可靠性与稳定性，但同时也会导致元件设计趋于保守，不能充分发挥其结构性能，针对此类问题，则可采用优化设计理论和计算机辅助工程软件加以解决。

　　3.1参数相关性分析

　　参数灵敏度分析可以系统地反映输入变量对输出变量的影响程度，即设计变量对输出变量的敏感程度，进行灵敏度分析不仅有助于确定输入变量灵敏度水平的高低，同时也可以保证最优解的稳定性，有助于迭代尽快收敛，当其计算方法如下：

　　式中：S为灵敏度水平；f(xi)为输出变量；xi为输入变量。

　　以横梁式测力仪最大应变量差为输出变量，以其结构设计参数为输入变量，则其参数相关性计算结果如图6所示。由图可知，参数P1对应变差影响较大，应变差随着参数P1即圆半径的增大而增大；P2即矩形的宽度对应变差影响较低，呈正相关；P3对最大应变差之影响水平最高，即随着矩形高度的增加，应变差随之增加，P4、P5影响水平较低，但均与最大应变差呈正相关。

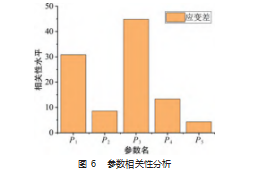
　　3.2优化实验设计

　　响应面优化属于一种全局类优化算法，其突破了传统的响应关系限制，可以更加直观地反映参数之间的相应关系，并采用多元二次回归拟合对数据进行处理，通过适当的优化算法对其进行采样得到理想的解，可以较好地预测实验结果，其数学模型如下[12]：

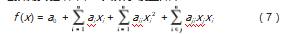
　　式中：n为设计变量个数；y(x)为拟合函数；a0、aii、ajj为待定系数；x 1~xn为设计变量。

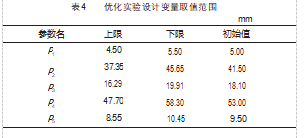
　　其优化实验过程中设计变量取值范围如表4所示。

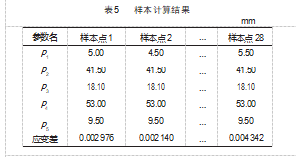
　　在响应面优化方法当中，提供了多种样本生成方法，其适用于不同的变量数与水平数目，此次实验只涉及3个输入参数，且样本样本水平差异较小，故而采用中心复合设计方法生成，样本数及计算结果如表5所示。

　　3.3实验结果分析

　　采用Design Expert对样本数据进行多元二次回归拟合，可以近似真实地表征输入变量与输出变量之间的响应关系，关于最大应变差与输入参数之间的拟合结果如下：

　　f(x)=0.002 8+0.001 0x 1+0.000 3x2+0.001 5x3+0.000 1x4+0.000 2x 1 x2+0.000 8x 1 x3-0.000 2x 1 x5+0.000 2x2 x3-0.000 3x2 x4-0.000 7x3 x5+0.000 1x4 x5+0.000 4x+0.000 1x+0.000 4x-0.000 5x-0.000 3x

　　经计算上述回归模型P=0.000 5<0.01，表示回归模型显著性水平较高，R2=0.954 2，R=0.909 5，表明方程拟合程较好，模型信噪比为10.863，该方程可以用来预测称重传感器弹性元件的应变值[13]。

　　对于优化问题的求解，其数学模型如下[14-15]：

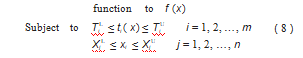
　　式中：TiL为状态变量的下限；TiU为状态变量的上限；XiL为设计变量的下限；XiU为设计变量的上限。

　　以平行梁式称重传感器最大应变量为目标函数，以其模态频率及最大应力为状态变量安全系数为约束条件，考虑到因应力集中等问题造成的结构刚度损失，此处选取屈服极限的安全系数为1.3，则关于平行梁式称重传感器的优化模型如下：

　　4优化实验结果分析

　　采用软件后处理自带的MOGA方法(多目标优化遗传算法)对优化问题进行求解，当目标函数符合优化要求，函数值达到最优，可认为此时设计参数已经满足优化要求，此时迭代终止，其优化结果如表6所示。

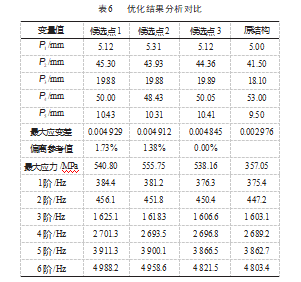
　　经优化设计共得到3个候选点，且3个候选点均服从状态变量约束，其应变差值大小接近，但候选点3偏离方程求解的参考值最小，故选择候选点3作为最优解。经优化设计弹性单元体上下表面的应变差较原结构增加了0.001 869，其固有频率与初始结构相比变化水平很小，结合式(2)计算可知，其灵敏度参提高了62.80%，结合式(3)计算可知其测量误差降低了38.56%，且其模态频率较原始结构均有大幅度提高。

　　5结束语

　　首先，在此次研究中首先根据弹性单元体的实际尺寸建立了5种结构形式弹性单元体的三维模型，并结合两项基本原则建立了其有限元模型，对其在固有频率和应变差进行了计算，计算结果表明应变差与其固有频率之间为反比例关系，与前人研究结论一致，验证了此次方针的准确性。

　　其次，经综合考量选择圆形结构为研究对象，经计算圆环结构在额定载荷下，其上下面应变差为0.002 976，最大当量应力为357.05 MPa，其前6阶固有频率为375.4、447.2、1 603.1、2 689.2、3 862.7、4 803.4 Hz。

　　最后，对弹性单元体进行结构优化，采用中心复合设计方法生成了28个样本点，结合最优化理论和多目标遗传优化算法对结构进行优化，最终选择候选点3作为最优解，此时其上下面应变差为0.004 845，最大当量应力538.16 MPa，其满足状态变量约束，其应变量增加了62.80%，测量误差降低了38.56%，研究结果表明，弹性单元体有较大优化空间，对称重式弹性单元进行优化设计有助于提高其工作性能，降低测量误差。

　　参考文献：

　　[1]Yaldiz Suleyman,Unsacar Faruk,Haci Saglam,et al.Design,Devel⁃opment and Testing of a Four-Component Milling Dynamometer for the Measurement of Cutting Force and Torque[J].Mechanical Systems and Signal Processing,2006,21(3):1499-1511.

　　[2]Panzera T H,Souza P R,Rubio J C C,et al.Development of a Three-Component Dynamometer to Measure Turning Force[J].International Journal of Advanced Manufacturing Technology,2012,62(9-12):913-922.

　　[3]赵友,葛晓慧,赵玉龙.高精度动态切削力自感知智能刀具的研究[J].机械工程学报,2019,55(21):178-185.

　　[4]龚中良,游江辉,梁力,等.梁式称重传感器弹性体的固有频率的提高及结构参数优化[J].传感器与微系统,2019,38(8):29-32.

　　[5]赵瑞杰,王鹏,王楠,等.三维切削力测力仪结构的多目标优化设计[J].陕西理工大学学报(自然科学版),2020,36(3):14-20.

　　[6]王娟,徐宏海,白传栋,等.基于ANSYS的三维动态切削测力仪的结构优化[J].机械设计与制造,2010(4):158-160.

　　[7]Uddin M S,Dong Songyi.On the Design and Analysis of an Octag⁃onal-Ellipse Ring Based Cutting Force Measuring Transducer[J].Measurement,2016,90(8):168-177.

　　[8]Sheikh Ahmad J Y,Ali D,Meng F.Design and implementation of a force dynamometer for friction stir welding[J].Arabian Journal for Science and Engineering,2018,43(9):4649-4657.

　　[9]杨进德.时效工艺对17-4PH不锈钢组织与力学性能的影响[J/OL].热加工工艺:1-4[2022-12-23].

　　[10]程玉阶.复杂机械系统动力分析[J].华中农业大学学报,1995(4):408-414.

　　[11]李克钢,王庭,秦庆词,等.基于修正最小应变能密度因子准则下的Ⅰ型裂纹研究[J].应用力学学报,2020,37(6):2664-2670.

　　[12]王昱彤,张星,张泽浩,等.基于响应面法的PBO纤维分散优化工艺探讨[J].合成纤维,2022,51(12):5-9.

　　[13]邢晓芳,贲强,周勇,等.基于回归分析的螺母凸焊工艺优化[J].焊接学报,2020,41(12):91-96.

　　[14]薛旭东,赵知辛,王琨.小麦脱皮机转子预弯工艺及优化设计[J].中国农机化学报,2020,41(3):104-108.

　　[15]赵知辛,薛旭东,薛琳婧,等.基于镜像对称补偿技术的脱皮机转子结构优化研究[J].机电工程,2021,38(6):774-780.

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/66101.html