SCI论文(www.lunwensci.com)
摘要 :针对目前笼筋成型生产中, 劳动强度大 、笼筋成型精度差 、难以实现自动化装配等突出问题, 对笼筋成型自动化生产过程 中头板 、端板的螺栓孔对正这一关键技术进行研究, 提出一种应用于笼筋自动化装配系统的图像识别模型 。首先由相机对端板进 行拍摄, 随后计算机读取图片并进行去噪, 经过数据变换后得到符合神经网络输入要求的图像数据 。利用这些数据对采用 BP 算法 建立的神经网络模型进行训练, 从而获得符合要求的模型及模型参数 。利用 Python 进行编程实现上述过程, 实验结果表明, 标准 BP 算法虽然能较为准确地识别出螺栓孔的位置, 但性能有时不稳定 。采用动量算法对其进行改进后, 模型性能和稳定性均获得一 定提升 。与传统人工装配相比, 应用该模型的系统能有效减少人力的使用, 有助于实现笼筋装配的自动化。
关键词 :笼筋自动化装配,神经网络,图像识别,自动化控制
An Image Recognition Model Applied to Automatic Assembly System of Cage Bar Chen Xiuxiang, Xu Hongbo
(School of Mechanical Engineering, Jiangsu University, Zhenjiang, Jiangsu 212013. China)
Abstract: In view of the prominent problems such as high labor intensity, poor forming accuracy and difficulty in automatic assembly in the
production of cage bars, the key technology of bolt hole alignment of head plate and end plate in the automatic production of cage bars are
studied, and an image recognition model applied to automatic assembly system of cage bar is proposed . The camera takes pictures against the
end board at first, and then the computer reads and de-noises the pictures. After data transformation, the image data conforming to the input
requirements of the neural network is obtained. By using these data, the neural network model established by BP algorithm is trained, so as to
obtain the model and model parameters that meet the requirements. Python is used to program the above process. Experiment results show that
although the standard BP algorithm can accurately identify the location of the bolt hole , its performance is sometimes unstable. The
performance and stability of the model are improved by momentum algorithm . Compared with the traditional manual assembly, the model
system can effectively reduce the use of manpower and help realize the automatic assembly of cage bars .
Key words: automatic assembly of cage bars; neural network; image recognition; automatic control
引言
预制混凝土桩是建筑行业中广泛使用的桩基础用材, 预制桩生产过程分为多个工作区, 包括装笼区 、端板装 配区等[1] 。 自动化程度较低, 批量装配时频繁起吊不仅 浪费时间, 还增加了劳动强度, 导致装配效率低[2]。
目前关于笼筋的自动装配的研究不多, 杨余明等[3] 提出一种预制桩笼筋与头尾板装配系统, 用于将头板、 尾板以及端板组装成端板组件 。该系统只是将端板 、头 板装配在一起形成组件, 而并未将其装配在笼筋主体上。 阙伊亮[4]提出利用带有卡盘的装配机夹住端头板的内孔 或外圆, 通过平移和旋转实现对中 。但由于笼筋由 V 形 台固定, 因此批量生产时需要频繁吊装, 导致大部分时 间都被消耗在吊装上 。周玉石[5]设计了一种榫卯装配式 预制桩结构, 采用榫卯结构加快了装配的速度 。以上几 种装配方式均是利用纯机械结构实现, 对于不同尺寸、不同结构的笼筋需要对机械结构进行重新设计, 因此适 用范围较狭窄。
为了解决笼筋成型生产过程中, 装配工劳动强度大、 通用性差 、难以实现自动化等突出问题, 本文提出了一 种图像识别模型应用于自动化装配系统方案 。系统工作 时, 由相机对端板进行拍摄, 随后计算机对得到的图片 进行读取, 对图片进行去噪, 经过数据变换后得到符合 神经网络输入要求的图像数据 。利用这些数据对采用 BP 算法建立的神经网络模型进行训练, 从而获得符合要求 的模型及模型参数 。实验结果表明, 该系统识别准确率 较高, 能够满足装配要求, 有利于生产企业的转型升级, 提高生产效率。
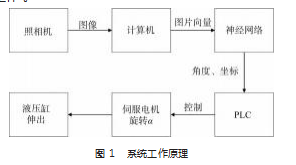
1 系统设计和工作原理
系统硬件部分由照相机 、PLC 、伺服电机和液压缸 组成, 用以完成图片的输入 、位置的接收 、孔的对正和接近, 方便进行装配工作 。系统的软件部分是基于 Py‐ thon 编程语言的 BP 人工神经网络, 以此实现图像识别的 功能, 从而完成图像的输入 、图像处理 、孔的位置输出 等功能。
系统工作原理如图 1 所示 。系统工作时, 首先由照 相机对端板进行拍照, 随后软件读取端板的照片, 处理 后输入神经网络, 神经网络计算识别后, 输出端板最高 处的孔的坐标, 通过输出的坐标计算出端板最高处的孔 与 y 轴正向的夹角 α, PLC 控制伺服电机旋转角度 α, 伺 服电机带动安装在其上的头板旋转同样的角度 α, 从而 实现螺栓孔的对正, 随后液压缸伸出, 将头板与端板 贴紧, 最后由螺栓拧紧机构将螺栓依次拧紧, 完成装 配工作 。
2 图像数据
2.1 张量获取
一张彩色照片 (如 32pixel×32 pixel) 可以看成一个 32 pixel×32 pixel×3 的张量, 存储着 R 、G 、B 三种不同颜 色通道的灰度值, 每个像素点有 8 位, 其值从 0 一直变化 到 255 。利用安装在支架上的照相机拍摄笼筋端板的照 片, 将此照片传入计算机, 再利用软件进行读取, 即可 实现图像张量的输入。
2.2 图像去噪
图像去噪的方法有很多, 较为常用的方法有均值滤 波和高斯滤波。
( 1 ) 均值滤波
均值滤波顾名思义, 其去噪的过程就是取平均值的 过程 。具体的操作步骤如下: 以目标像素点为中心点, 使用一个窗口框选目标像素点周围的像素点, 然后对处 于窗口内的所有像素点求均值, 该均值即作为目标像素 点去噪后的像素值。
( 2 ) 高斯滤波
所谓高斯滤波, 可以看成是一种特殊的均值滤波 。 在均值滤波中, 窗口中的所有像素点在参与计算时都有 相同的权重, 而这会造成去噪后的图像变得模糊 。高斯 滤波则是将靠近目标像素点的像素点的权重提高, 越靠 近则权重越高, 然后计算窗口内所有像素点的加权平均 值, 并将该值作为目标像素点去噪后的新值。
2.3 图像数据的输入
经过读取照片和图像去噪后, 可以得到一个与图片 相对应的张量, 如果按照一定的次序, 将这一张量排成 一列, 变成一个向量, 就可以在图片与向量之间建立起一 一对应的映射关系, 从而完成最终的图像数据准备工作。
3 BP 算法
3.1 算法步骤
算法的具体步骤如下。
( 1 ) 根据数据和权重与偏置的初始值, 进行前向计算, 得到各层的激活函数值 a(l), 当 l = 1 时, a(l)就是输 入 x。
( 2 ) 以二次代价函数 (不考虑正则项) 为例, 对于 全部样本, 有如下代价函数:
3.2 相关改进算法
虽然 BP 算法可以解决一些非线性问题, 但它也存在 着一些问题, 如容易陷入局部最优解 、收敛速度慢等 。 为了解决这些问题, 人们又提出了许多改进方法以期提 升模型效果, 这些方法大致可以分为如下几类: 改变增 量 (梯度和学习率), 改变代价函数, 改变激活函数等 。
3.2. 1 改变增量
根据增量更新时使用的样本数目的多少, 梯度下降 算 法 可 以 分 为 批 量 梯 度 下 降 ( BGD )、 随 机 梯 度 下 降 ( SGD ) 以及小批量梯度下降 ( MBGD )。 SGD 算法是一 种很重要的优化算法[6], 经常被用来训练各种模型[7], 而 采用 SGD 算法来更新参数的 BP 算法更是常被称为训练人 工神经网络的标准算法[8] 。虽然 SGD 算法应用的很广, 但是其缺点也很明显, 即若想要快速收敛, 就要加大学习率, 但这样会导致模型不稳定[9], 模型效果波动性太 高 。若想要模型稳定, 就要减小学习率, 可这样又会导 致模型训练变得非常耗时 。这样的两难问题, 采用基于 momentum 的梯度下降算法[10]通常可以获得较好的解决或 改善 。具体如下。
为了直观地理解算法之所以起作用的原因, 可以将 Δw 视为速度, 将 ∇C 视为加速度, 通过引入超参 α, 就 可以减小速度因某些“错误”样本所引起的变化, 使得 w 可以继续朝着正确的方向前进, 即使参数具有一定的 “惯性”,从而起到防止震荡 、加快收敛的作用。
动量算法常常被研究人员用来训练人工神经网络[12], 并且可以与其他的算法 (如模拟退火算法) 相结合[13] 。
3.2.2 改变代价函数
常见的二次代价函数在线性回归中经常使用, 但 是对于使用"S"型激活函数的神经网络而言, 二次代价 函数往往会导致代价函数很大, 但其下降速度却很慢 的问题。
( 1) 交叉熵代价函数
对于单个神经元, 交叉熵代价函数定义如下:
( 2) 正则化代价函数
当网络规模较大时, 常常会出现模型在训练集上表 现得很好, 但是在测试集上表现得很糟糕的现象, 这种 现象称为过拟合现象[14] 。出现这种现象, 表明模型几乎 在单纯地记忆训练集, 而不是发掘隐藏在数字背后的本 质, 即模型的泛化能力不足 。尽管增加训练样本或减小 网络规模可以减轻过拟合的程度, 但训练数据通常较难 获得, 而大的网络又拥有比小网络更强的潜力, 故两种 方法都不适合采用 。为了防止过拟合, 提高模型的泛化
式中: Cx 是对每个训练样本的代价函数 (未正则化的); m 为小批量样本数, 求和是在小批量样本上进行的 ( m 个求和)。
由正则化后的代价函数通式可以看出, 在使 C0 相等 的情况下, 正则化模型更倾向于选择更小的权重 。小的 权重意味着网络不会因为输入值的微小变化而发生太大 的改变, 可以理解为对噪声不敏感 。而大权重的网络, 由于权重较大, 即使是小的噪声, 也会被模型捕捉, 使 模型产生较大的变化, 从而使模型成为包含大量噪声的 复杂模型[16], 也就是过拟合。
虽然, 正则化在理论方面还不够完善, 但是许多实 验事实表明正则化模型的泛化能力要比未正则化模型强。 故正则化也不失为一种好的改善模型性能的方法。
3.2.3 改变激活函数
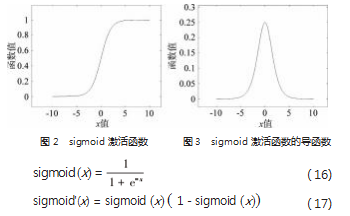
( 1) sigmoid 函数
在机器学习中, 常使用 sigmoid 函数作为激活函数, 其表达式如式 ( 16) 所示, 图像如图 2 所示 。sigmoid 激 活函数的导函数的表达式如式 ( 17) 所示, 图像如图 3 所示 。从图中可以看到, 当输入值 z 较大时, sigmoid 的 导函数值趋近于 0. 而这会导致起步梯度消失的问题 。 3.2.2 节介绍的交叉熵代价函数已经可以很好地解决这个 问题了, 但并不是一定使用交叉熵代价函数, 下面的激 活函数同样可以解决这个问题。
式中 α 为超参, 可以与其他神经网络参数一起训练[17]。
PReLU 函数是对 ReLU 函数缺点的些许改进, 可以 避免坏死的情况发生, 但同时也牺牲了一些泛化能力 。 参数 α 取固定值 0.01 的 PReLU 函数被称为 Leaky ReLU 函 数, 当 α 由 高 斯 分 布 随 机 产 生 时, PReLU 又 被 称 为 RReLU 函数。
以上对于激活函数的说明只是对激活函数性质的一 个大致描述, 在具体的模型当中, 不确定哪一个激活函 数表现得更好, 因为与正则化一样, 目前也还没有一个 足够坚实的理论能够为诸如“该如何选择激活函数”的 问题提供指导 。但还是可以通过感觉 、经验 、惯例或实 验等方式来决定到底选用何种激活函数 。尽管这往往会 给模型带来性能上的差异, 但在通常情况下, 这些性能 参差的模型也能得到一些令人感到满意的结果, 从而解 决一些问题。
3.3 神经网络设置
代价函数方面, 选择了无正则化项的二次代价函数, 因为其易于理解和计算 。激活函数方面, 选择了 PReLU 函数 ( α = 0.5 ), 目的是为了避免出现之前分析中所提及 的由于二次代价函数和"S"型激活函数的同时出现所引起 的一些问题 。算法方面, 分别使用了标准 BP 算法和动量 算法 。神经元和隐藏层数目方面, 输入层神经元数 3072 ( 32×32×3), 隐层数 1. 隐层神经元数 30. 最终输出为最 高处的孔的坐标。
通过在训练集上对上述神经网络进行训练, 不断迭 代层与层之间的权重与偏置, 从而提升模型在测试集上 的表现, 达到一定的准确率后, 模型即可停止训练, 投 入实际使用。
4 结果与分析
4.1 标准 BP 算法
采用 SGD 算法来更新权重和偏置, 学习率为 0.096 3. 在 10 次独立实验中, 模型有 8 次表现得非常好, 训练集 错误率收敛至 0.03. 测试集错误率收敛至 0.00. 全部预 测正确, 模型准确性相当好 。而剩下的 2 次, 模型似乎 表现得不太理想, 测试集错误率甚至达到了 0.44.
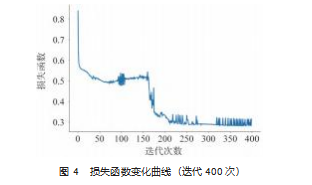
通过绘制迭代次数 ( 400 次) 更长的损失函数变化 曲线, 可以找到模型表现不好的原因: 由于模型初始值 是随机, 模型在参数空间的起始点也是随机的, 这导致 模型很容易陷入局部的最优解 。而之前的迭代次数固定 为 50 次, 模型在 50 次内很难走出局部最优解 (图 4 中, 62 次到达局部最优解, 迭代至 176 次左右才跳出), 从而 导致较高的错误率。尽管模型偶尔会遇到局部最优解, 导致性能不稳定, 但若延长迭代次数, 还是可以收敛至全局最优解的 。总 的来说, 模型表现得还是相当不错的。
4.2 动量算法
下面采用动量算法, 重复上述实验 。设置学习率为 0.014 5. 动量算法新增参数 α = 0.9 。使用了动量算法 后, 10 次独立实验中, 模型 10 次表现得都非常好, 训练 集错误率收敛至 0.05 左右, 测试集错误率收敛至 0.00. 全部预测正确, 模型性能相当好 。这表明, 使用动量算 法优化后, 模型不仅不易陷入局部最优解, 同时性能上 还更加优秀 、稳定。
5 结束语
本文针对笼筋生产过程中, 装配工劳动强度大 、通 用性差 、难以实现自动化等突出问题, 提出了一种图像 识别模型应用于自动化装配系统 。其主要功能及应用效 果如下。
( 1 ) 系统的数据输入, 采用无接触式拍照输入, 相 对于传统的机械式对准, 没有明显机械力, 既能保证不 对笼筋本身产生机械损伤, 从而提高笼筋的尺寸和形状 精度, 又有一定的通用性, 适用于各种尺寸 、各种形状 的笼筋主体。
( 2 ) 一方面进行了图像去噪处理, 另一方面采用了 鲁棒性和泛化能力更好的激活函数, 避免了图像噪声的 不良影响, 同时提升了模型的准确性 、鲁棒性和泛用性。
( 3 ) 利用动量算法对标准 BP 算法构建的神经网络模 型进行了改进, 提升了模型的准确性和可靠性, 带来了 较大的性能提升。
( 4 ) 相较于传统的人工装配线, 减少了人工的使用, 提高了生产效率和自动化 、智能化程度。
参考文献:
[1] 周 兆 弟 . 一 种 笼 筋 端 板 装 配 流 水 线 : 浙 江 , CN212145246U [P].2020- 12- 15.
[2] 尹红,钟日来,王迪伟,等 . 一种管桩笼筋装配自流平台:中国, CN208854837U[P]. 2019-05- 14.
[3] 杨余明,马进元,杨兴江,等 . 一种预制桩笼筋与头尾板装配系统及方法:中国,CN114101983A[P].2022-03-01.
[4] 阙伊亮 . 浅谈管桩生产设备的自动化改造[J]. 福建农机,2011 (1):45-47.
[5] 周玉石,谢晓东,谢益飞,等 . 一种榫卯装配式预制桩结构体系: 中国,CN216712998U[P].2022-06- 10.
[6] Bottou L. Online Algorithms and Stochastic Approximations[M]. Cambridge,UK:Cambridge University Press, 1998.
[7] Finkel J R, Kl Ee Man A, Manning C D. Efficient, feature- based, conditional random field parsing[C]// Acl, Meeting of the Association for Computational Linguistics, June, Columbus, Ohio, Usa. DBLP, 2008.
[8] Lecun Y A, Bottou L, Orr G B, et al. Efficient backprop[J]. Lec ‐ ture Notes in Computer Science, 1998:9-48.
[9] Toulis P, Airoldi E M . Asymptotic and finite-sample properties of estimators based on stochastic gradients[J/OL]. Eprint Arxiv, 2017. 45(4):1694- 1727.
[10] Nielsen M A. Neural networks and deep learning[M]. San Fran ‐ cisco, CA: Determination Press, 2015.
[11] Rumelhart D E, Hinton G E, Williams R J. Learning representa ‐ tions by back-propagating errors[J]. Nature, 1986. 323(6088): 533-536.
[12] Zeiler M D. Adadelta: an adaptive learning rate method[J/OL]. arXiv preprint arXiv:1212.5701. 2012.
[13] Borysenko O, Byshkin M. CoolMomentum: a method for stochas ‐ tic optimization by Langevin dynamics with simulated annealing [J]. Scientific Reports, 2021. 11(1): 1-8.
[14] Goodin D S . The cambridge dictionary of statistics[J]. Muscle & Nerve, 2015. 22(6):783-783.
[15] Ghosh J K. Statistics for High ‐ Dimensional Data: Methods, The‐ ory and Applications by Peter Bühlmann, Sara van de Geer[J]. International Statistical Review, 2012. 80(3):486-487.
[16] Burnham K P, Anderson D R. Model Selection and Multimodel Inference: a Practical Information-theoretic Approach[M]. 2nd edn. Springer-Verlag, New York. 2002.
[17] Delving Deep into Rectifiers: Surpassing Human-Level Perfor‐ mance on ImageNet Classification[C]// CVPR. IEEE Computer Society, 2015.
第一作者简介:陈修祥 (1975— ), 男, 安徽无为人, 博士, 副教授, 研究领域为智能机械 、机器人及自动化生产线设计, 已发表论文 10 余篇。
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/65483.html