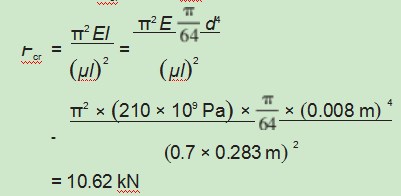SCI论文(www.lunwensci.com)
摘要:针对某型号电机转轴在冷压入轴工艺过程中转轴可能发生屈曲失稳风险的问题,对电机转轴进行了入轴屈曲分析。首先建立了理论计算模型,计算出了转轴的临界失稳压力,其次运用CAE仿真方法及相关软件,对实际的转轴结构进行了有限元屈曲失稳仿真分析,得到了临界失稳载荷的仿真值,仿真值和理论计算值比较接近,并分析了理论计算值和仿真值的差异原因,最后结合在电机转轴入轴现场试验中得到的实际入轴压力,计算了电机转轴的稳定因数,结果表明该电机转轴在入轴过程中的稳定安全因数满足稳定要求,且安全余量较大,不会发生屈曲失稳,可保证批量生产中也具有良好的稳定性。为电机在研发设计过程中关于转轴的压入稳定性提供了设计和校核指引,可在设计上有效避免电机装配时转轴入轴失稳风险问题。
关键词:电机转轴;屈曲失稳;临界压力;CAE仿真
Analysis and Application of Buckling Instability on Shaft of Motor
Wu Lihua,Kang Guopo,Huang Guohao,Li Jiecheng,Li Ketian
(Robotics Institute,Guangdong Open University(Guangdong Polytechnic Institute),Guangzhou 510091,China)
Abstract:Motor shaft rotation in the process of cold pressing into the shaft process has the risk of buckling instability problems,a buckling analysis is conducted on the motor shaft.Firstly,the theoretical calculation model is established to calculate the axis of the critical buckling pressure.Secondly,using CAE simulation method and related software,finite element buckling instability simulation analysis is conducted on the actual shaft structure,and the simulation value of the critical instability load is obtained.The simulation value is relatively close to the theoretical calculation value,and the reasons for the difference between the theoretical calculation value and the simulation value are analyzed.Finally,based on the actual input pressure obtained in the on-site test of the motor shaft,the stability factor of the motor shaft is calculated.The results show that the stability safety factor of the motor shaft during the input process can meet the stability requirements,and the safety margin is large,without buckling instability,which can ensure good stability in batch production.This provides design and verification guidance for the stability of the shaft during the research and development design process of the motor,which can effectively avoid the risk of shaft instability during motor assembly.
Key words:shaft of motor;buckling instability;critical pressure;CAE simulation
0引言
当细长杆受拉时的应力达到屈服极限或强度极限后,将引起塑性变形或断裂,而当细长杆受压时,却表现出与受拉时强度失效全然不同的性质,随着压力载荷的逐渐增大,细长杆开始是直线,接着是被压弯,发生较大的弯曲后最终被折断。这种受压长杆丧失其直线形状的平衡而过渡为曲线平衡的情况称为失稳,也称为屈曲,失稳时的压力称为临界压力。杆件失稳后,压力的微小增加将起引起弯曲变形甚至断裂失效,这种形式的失效并非强度不足,而是稳定性不够[1-2]。因此,在机械结构工程中,对于受压杆件和压缩部件等零部件,不仅需考虑强度问题,还需考虑屈曲失稳。
国内外很多学者针对屈曲失稳从理论计算分析和CAE仿真分析的角度进行大量研究。文献[3-8]借助有限元工具对特征屈曲分析和非线性屈曲分析求解压杆屈曲荷载的适用性进行了研究,也分析了几何参数对长臂、细长杆等多种结构的屈曲临界的影响。文献[9-11]对截面为圆环型的管路的严重失稳问题进行了线性屈曲分析和非线性屈曲分析后,发现钢管失稳破坏的主要原因是径向刚度不足,通过管路材质变更等提高管路径向刚度的措施可解决其失稳问题。文献[12-14]首先对钻杆和桁架结构进行了屈曲稳定性分析以及模态分析,然后根据分析结果对相关结构进行了改进设计,使其在满足刚度与强度的前提下,实现了轻量化设计的目标。
在家用电机的转子组件中,转轴和转子铁心之间的配合一般均为过盈配合,并采用冷压入轴工艺进行安装,该安装工艺导致转轴在压入的过程中会承受较大的轴向压力,而家用电器的转轴结构通常呈细长杆状,会使得转轴在压入的过程中不仅有发生永久塑性变形的风险,还有发生屈曲失稳的风险,故在设计时需要进行稳定性校核,保证结构设计的合理性。
1入轴失稳临界压力理论计算
若电机转轴的入轴压力达到或超过失稳临界压力后,转轴在压入过程中将由直线平衡状态转变为曲线平衡状态,会造成转轴失稳,从而影响入轴工艺,故在设计转轴时有必要计算出电机转轴入失稳的临界压力,以确保实际入轴压力小于该临界压力值,避免冷压入轴失效。
以某型号家用电器的电机转轴为例,转轴是钢制实心细长圆柱体,轴上开有扁位、凹槽和倒角等。最大轴径ϕmax=8 mm,最小轴径ϕmin=6 mm,轴长L=283 mm。转轴冷压入转子铁心时有发生屈曲失稳的风险,需计算失稳临界压力载荷以进行稳定性校核。
该电机转轴的材料为45号钢,其弹性模量E=210GPa,屈服强度σs=355 MPa,比例极限σp=280 MPa。
1.1模型简化
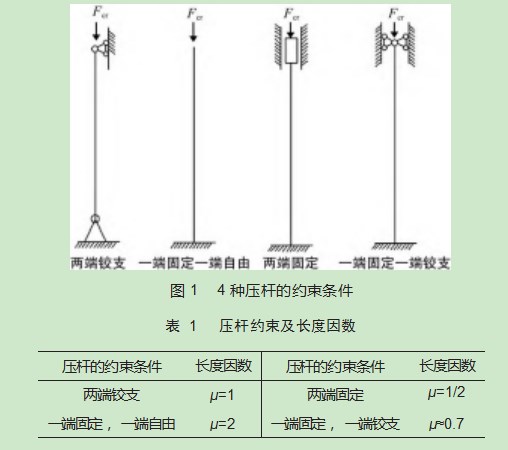
根据材料力学[15]中的简化原则,可以将三维实体的转轴简化为一维的杆件,同时将入轴时的装夹约束条件简化成如图1所示的4种情况之一:(1)两端铰支;(2)一端固定、另一端自由;(3)两端固定;(4)一端固定、另一端自由。其各自对应的长度因数如表1所示。
转轴在冷压入轴工艺过程中一端用装置夹紧,另一端置于转子中心孔附近,压装机开始工作后将转轴压入转子的中心孔内。根据转轴在冷压入轴工艺过程中装夹的实际情况,可将转轴的入轴过程约束条件简化为表1中的一端固定、一端铰支的压杆,故长度因数μ=0.7。
1.2临界压力计算
临界压力Fcr的计算是采用欧拉公式[15],其计算公式为:
这是欧拉公式的普遍形式,式中μl表示把压杆折算成两端铰支杆的长度,称为相当长度,μ是长度因数。
用Fcr除以压杆的横截面积A,得到临界压力对应的应力σcr为:
把横截面的惯性矩I写成I=1-i2A的形式,i为截面的惯性半径,这样式(2)就可以写成如下形式:
引入λ=μl/i,λ是一个量纲一的量,称为柔度或长细比,它集中反映了压杆的长度、约束条件、截面尺寸和形状等因素对临界应力σcr的影响。而转轴的截面是圆形,其截面的惯性半径i==d/4,则转轴的柔度λ的计算公式可以写成如下形式:
欧拉公式是由弯曲变形的微分方式导出的,而材料服从胡克定律又是上述微分方程的基础,所以只有临界应力σcr小于比例极限σp时,欧拉公式才能正确使用。可见,只有当压杆的柔度λ(长细比)大于或等于材料的极限柔度λ1时,通过式(1)所计算出来的临界压力值才是正确的,否则不能使用式(1)进行计算,材料的极限柔度λ1的计算公式为:
综上所述,分别在式(4)和式(5)代入相关已知数据,计算出λ=99.1,λ1=86,即λ>λ1,电机转轴为大柔度压杆,本文中所研究的电机转轴受压入轴的临界压力可用欧拉公式计算,在式(1)中代入已知数据,计算出临界压力Fcr=10.62 kN,即:
2 CAE仿真计算
在前面临界压力的理论计算中,对转轴的模型进行了简化,将转轴实际的3D模型简化成了一维的杆件单元,并忽略了扁位、凹槽和倒角等特征的影响,理论计算模型偏理想化,不能考虑结构细节和应力集中的影响,故理论计算值会与实际结果存在较大的差异;此外,还对入轴过程中的约束条件进行了相应的简化,比如将面约束简化为点约束、面力简化为集中力等,为了更加详细分析电机转轴在入轴过程中的情况,因此非常有必要利用CAE软件来计算接近实际入轴时的失稳临界载荷[16-18]。
2.1屈曲失稳分析
屈曲失稳分析分为线性屈曲分析和非线性屈曲分析,在本文中将采用线性屈曲分析,其是以特征值为仿真研究对象,和材料力学上的压杆稳定法一样都是基于近似弹性理论的失稳分析方法,具有以下优点[3]:(1)求解时间短,能用第一步计算来评估临界载荷;(2)可以用来作为决定产生什么样的屈曲模态形状的设计工具,为设计做指导。
线性屈曲分析的一般方程[19]为:
式中:[K]和[S]为常量;λ为屈曲载荷乘子;{w}为屈曲模态形状系数。
2.2有限元模型
根据实际仿真分析需要,关心的重点为入轴过程中转轴的稳定度、强度和刚度问题,故对CAD模型进行了适当的简化,忽略了其他零部件,仅对转轴建立有限元模型来进行仿真分析,定义材料属性(弹性模量,泊松比),其有限元模型如图2所示。
2.3载荷和边界条件
根据转轴在冷压入轴工艺过程中装夹的实际情况和分析设置要求,入轴过程中的载荷和边界条件设置如图3所示,具体如下:
(1)在转轴上端一段圆柱面上施加固定约束;
(2)在转轴下端圆柱面上施加圆柱约束,限制轴向和周向的位移;
(3)在轴的下端圆柱面上施加1 N的初始力。
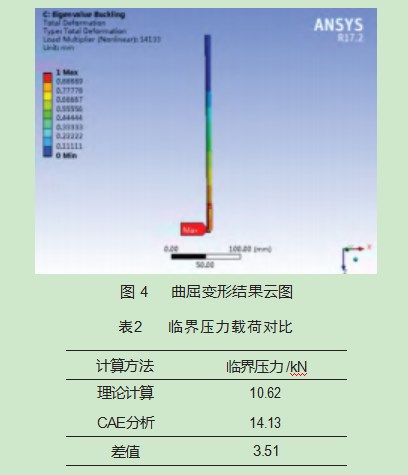
2.4分析结果
转轴的归一化变形结果云图如图4所示,由分析结果可以读出转轴发生屈曲失稳的临界压力Fcr=14.13 kN。临界压力的理论计算结果和CAE仿真计算结果的对比如表2所示,其与理论计算结果相对比较接近,但仍存在一定的差异,差值达3.51 kN,这主要是由于在理论计算中对计算模型进行了相应简化和理想化。
3入轴力测试及稳定性校核
在前面的研究内容中,已分别用理论计算和CAE仿真方法计算出了电机转轴入轴时失稳临界压力Fcr值,接下来对转轴压入过程的稳定性进行校核,一般用临界压力Fcr与最大工作压力Fmax之比即压杆的工作安全因数n来进行校核评判,其应大于规定稳定安全因数nst,即:
稳定安全因数一般要高于强度安全因数,这是因为有一些难以避免的因素(杆件的初弯曲、材料不均匀等)会降低临界压力而严重影响压杆的稳定。根据电机的实际运行工况及机械设计手册[20]规定,本文中规定稳定安全因数nst=3。
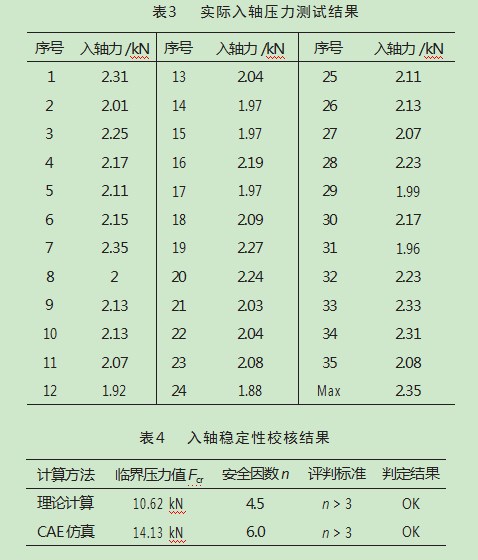
综上所述,对电机转轴的入轴压力值测试了35组试验数据,如表3所示,最大入轴压力值Fmax=2.35 kN,再根据式(7)分别计算出理论计算的临界压力和CAE仿真的临界压力所对应的电机转轴的稳定安全因数分别为4.5和6.0,结果如表4所示。从表中可以得出,无论是采用理论计算还是CAE仿真分析计算获得的临界压力Fcr计算出的安全因数n,均满足稳定性要求且安全余量较大,不会发生屈曲失稳,可保证电机在批量生产过程中转轴在压入时具有良好的稳定性。
4结束语
本文对某型号电机转轴在冷压入轴工艺过程中转轴可能发生屈曲失稳的风险问题,对电机转轴进行了稳定性校核。首先采用理论计算的方法,计算出了转轴的临界失稳压力是10.62 kN,然后运用CAE仿真方法对实际的转轴结构进行了有限元屈曲失稳仿真分析,得到了失稳临界载荷的CAE仿真值是14 kN,仿真值和理论计算值比较接近,并分析是理论计算模型的简化处理造成了失稳临界载荷在理论计算和仿真计算上的差异。
为验证理论计算和CAE仿真结果的准确性,针对电机转轴入轴进行了35组试验,测试所得到的实际入轴压力的最大值Fmax=2.35 kN,计算出电机转轴的稳定因数(理论计算4.5和CAE仿真6.0),均大于许用稳定安全因数(nst=3)。结果表明该电机转轴在入轴过程中的稳定安全因数满足稳定要求,且安全余量较大,不会发生屈曲失稳。本文的研究内容为电机在研发设计过程中关于转轴的压入稳定性提供了设计和校核指引,可在设计上有效避免电机装配时转轴入轴失稳风险。
参考文献:
[1]张文静,刘学文,张卜.压杆屈曲行为的突变理论分析[J].数学的实践与认识,2020,50(22):208-215.
[2]伍建军,汪辉,欧阳丹,等.精密定位平台柔性支撑杆屈曲分析[J].组合机床与自动化加工技术,2017(6):26-29.
[3]高瑞杰,唐军.压杆稳定的特征值法与非线性法的适用性评价[J].钢结构,2016,31(1):5-8.
[4]姚峰林,佘占蛟,孟文俊,等.超起装置对伸缩臂屈曲分析的影响[J].现代制造工程,2018(6):18-22.
[5]刘海洋,李栻曦,牛斌.加筋圆筒结构重量和屈曲承载力关系的量化分析[J].机电工程技术,2023,52(3):121-125.
[6]黄中华,刘喆,谢雅.超大功率风力发电机组塔筒屈曲分析[J].太阳能学报,2022,43(4):304-310.
[7]甘泉,韩伟,沈佳铭,等.基于ANSYS Workbench的细长压杆屈曲分析研究[J].石化技术,2017,24(1):46-47.
[8]刘湘龙.细长柔性压杆弹性失稳的后屈曲分析[J].科技风,2013(21):149-150.
[9]潘艺昌,李金泽,谭文慧,等.海水淡化取水系统管路失稳分析及改进[J].水处理技术,2022,48(10):68-71.
[10]Xu Leige,Lin Mian.Numerical study on critical axial forces of upheaval buckling for initially stressed submarine pipelines on uneven seabed[J].Ocean Engineering,2017.
[11]涂从刚,孔垂雨,杜蔚琼.基于ANSYS的某电站压力钢管失稳破坏原因分析[J].水利技术监督,2022(9):153-156.
[12]李雷.旋挖钻机钻杆系统结构分析及优化设计[D].秦皇岛:燕山大学,2020.
[13]高翔,张烁,张贝贝,等.基于ANSYS的浮空器组阵结构屈曲分析及优化设计[J].电子机械工程,2022,38(2):19-22.
[14]屠凤莲,范顺成,罗文龙.基于ANSYS的支撑架特征值屈曲分析[J].河北工业大学学报,2010,39(3):6-10.
[15]刘鸿文.材料力学Ⅰ[M].6版.北京:高等教育出版社,2017.
[16]余娟,余明友,金建伟,等.基于ANSYS的天线杆屈曲分析[J].计算机与数字工程,2013,41(9):1523-1524.
[17]康元顺,张伟为,刘梦娟,等.基于牛顿迭代算法的大型有面外支撑杆X撑结构的屈曲分析[J].工程力学,2022,39(S1):286-295.
[18]黄浩,刘明亮,龚明成,等.基于有限元的某机型连杆结构分析[J].内燃机,2018(6):58-62.
[19]李丹,曾翠华.基于有限元法的传动丝杠模态及线性屈曲分析[J].机械,2017,44(2):14-16.
[20]闻邦椿.机械设计手册第六卷[M].5版.北京:机械工业出版社,2010.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网! 文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/64997.html