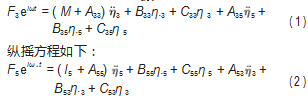SCI论文(www.lunwensci.com)
摘要 :利用切片理论研究 KVLCC2 船模在波浪上的运动响应和附加阻力, 有助于研究船舶耐波性, 同时也能丰富切片理论的研究 成果 。以 KVLCC2 船模为研究对象, 利用切片理论, 研究了 KVLCC2 船模在斜浪中的响应幅值算子曲线 、波浪增阻以及运动响应。 结果表明, 基于切片理论的计算值与实验值总体上吻合良好, 证明了切片理论对于船舶在波浪中的计算有较高的精度 。相同波长 下高航速的垂荡响应明显大于低速, 这意味着船舶需要提供更多的能量来克服垂荡运动所引起的能量损耗 。 当船舶在迎浪和艏斜 浪中航行时, 降低航速可以有效地减小附加阻力; 而当船舶在艉斜浪中航行时, 适当增大航速可以一定程度上减小附加阻力。
关键词 :KVLCC2,波浪增阻,运动响应
Study on the Motion Response and Added Resistance of KVLCC2 in Oblique Waves
Zhao Bowen1. Zhang Dapeng2. Yan Jin2
( 1. Ocean College, Zhejiang University, Zhoushan, Zhejiang 316021. China;
2. Ship and Maritime College, Guangdong Ocean University, Zhanjiang, Guangdong 524088. China)
Abstract: Using the strip theory to study the motion responses and additional resistance of KVLCC2 ship model on waves is helpful to study
the seakeeping performance of the ship, and can also enrich the research results of the slice theory. The KVLCC2 ship model is taken as the
research object, and strip theory is used to study the RAO curves, added resistance, and motion response of the KVLCC2 ship model in oblique
waves. The results indicate that the calculated values based on the slice theory are generally in good agreement with the experimental values .
The heave response at high speeds is significantly greater than that at low speeds at the same wavelength , which means that the ship needs to
provide more energy to overcome the energy loss caused by heave motion . When the ship is sailing in waves and bow waves, reducing the speed
can effectively reduce the added resistance. When the ship is sailing in oblique waves at the stern, increasing the speed appropriately can
reduce the added resistance to a certain extent.
Key words: KVLCC2; added resistance; motion response
引言
耐波性是指船舶在海上遭受风浪流的干扰, 产生各 种摇摆运动以及抨击 、飞溅 、失速等强非线性现象后, 仍 能 保 持 其 原 本 性 能 (如 稳 性 、结 构 强 度 等) 的 能 力[1-3] 。研究船舶适航性和耐波性, 首先要解决的就是船 舶在波浪中的运动问题, 这同时也是船舶设计建造中要 解决的关键技术问题[4-6]。
在早期的研究中, 船舶设计人员仅考虑了入射波对 船体的干扰力, 并未涉及船体本身及其运动对周围流场 带来的干涉, 这部分波浪干扰力就是傅汝德-克雷洛夫 力 (Froude-Krylov Force)。 随着频谱和高性能计算技术 的有效提升, 有关船舶在波浪中的运动理论也得到了快 速发展[7-9], 一些成熟的理论和计算方法逐渐吸引了船舶 设计人员的注意, 这其中有基于假设条件的切片理论[10] 和高速细长体理论[11] 、基于混合源方法的三维频域理论 和三维时域理论[12- 13]以及非线性理论等[14] 。切片理论是耐波性研究的重大突破, 这一方法到现在仍被广泛地应 用在船舶设计实践中[15- 18]。
KVLCC2船模是国际公认的标准模型, 具有详细的 试验数据, 多用于船舶耐波性及操纵性的试验验证, 如 深水及浅水中的流场测量实验研究[19-20] 。利用切片理论 研究 KVLCC2船模在波浪上的运动响应和附加阻力, 有 助于研究船舶耐波性, 同时也能丰富切片理论的研究成 果 。基于此, 本文以 KVLCC2船模为研究对象, 利用切 片理论, 研究船模在斜浪中的运动响应和附加阻力, 以 期为船舶耐波性的研究提供借鉴和参考作用。
1 切片理论
切片理论的核心是将船体分解为多个横向薄片, 每 个薄片都被视为无限长柱体的一个横剖面, 通过二维绕 流理论确定下每个剖面的水动力学系数后, 再沿船长积 分得到整个船体的受力。
船舶的垂荡和纵摇运动均包含由浮力变化产生的恢复力, 因此两个运动中均是振荡的 。垂荡方程如下:
运 动 方 程 中 的 各 个 系 数 的 计 算 过 程 如 式 ( 3 ) ~ ( 13 ) 所示:
当船舶振荡被约束后, 出现入射波时的载荷被称为 波浪激振力和力矩 。波激力和力矩是诱发船舶运动响应 的主要因素 。波激力和力矩由下式给出:
式 ( 1 ) ~ ( 17 ) 中: M 为船舶质量; I 为惯性矩; A 为附 加质量系数; B 为阻尼系数; C 为静水恢复力系数; η 为 平移值/角度值; F 为波激力/力矩; a33 为截面附加质量; b33 为截面阻尼; b 为截面宽; g 为重力加速度; U 为船 速; ζ为与 LCB的纵向距离;f3 为 Froude-Krilov 力; h3 为
2 数值模型
KVLCC2 船模的几何模型如图 1 所示, 设计水线长 5.6 m, 最大船宽 1 m, 吃水 0.319 m, 排水体积 1.404 m3. 湿表面积 7.837 m2.
波浪工况共有 7 个, 浪向角μ 分别为 0° 、30° 、60°、 90° 、120° 、150° 、180° 。航速共有两个, 分别是以 35° 舵角稳定回转时的航速 Fn=0.055 和设计工况下的航速 Fn =0. 142. 对应 0.408 m/s 和 1.047 m/s。
截面数为41. 船体水下部分的切片划分情况和映射关 系如图2~3 所示, 红色线为船体截面, 绿色线为映射截面。
3 计算结果分析
3.1 RAO 曲线
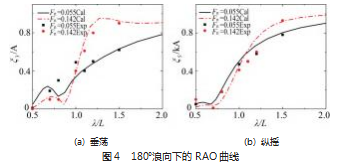
图 4 所示为 KVLCC2船舶迎浪航行的 RAO 曲线, 将 切片理论的计算结果与实验值进行对比, 实验数据来自 Min Seo 在 2021 年的研究成果[21] 。作用在船舶上的波浪力 主要受船舶运动响应以及周围波场的影响, 因此, 准确 预测船舶的运动响应对于波浪力的计算至关重要 。 由图 可知, 基于切片理论的计算值与实验值总体上吻合良好。 在波长小于船长的短波条件下, 垂荡计算值与实验相差较大, 当波长大于船长时, 垂荡计算值与实验值比较接 近 。纵摇运动的计算曲线总体上没有出现与实验值偏差 较大的部位。进一步观察图 4 可知, 当波长船长比 λ/L<1 时, 航速 Fn=0. 142 的运动响应要弱于 Fn=0.055 。当 λ/L>1 时, 航速 增大带来了垂荡和纵摇运动的显著增加 。航速 Fn=0. 142 时, 垂荡响应曲线随着波长的增大先是快速升高, 到达 峰值后有小幅度下降; 纵摇响应在 0.75<λ/L<1.5 的波长 段快速增大, 而后增幅有所减弱 。随着航行速度的增加, 遭遇频率高于波浪频率, 船舶周围的散射波场也随之改 变。因此, 船舶的运动特性会根据相同波长的船速而改变。 图 5 所示为不同浪向下 KVLCC2船舶的垂荡和纵摇 RAO 曲线 。对于垂荡运动, 浪向角为 150°下, 当波长小 于船长时, 两种航速的垂荡响应差距不大; 当波长大于船长时, 航速的改变带来了垂荡响应的显著改变 。相同 波长下高航速的垂荡响应明显大于低速, 这意味着船舶 需要提供更多的能量来克服垂荡运动所引起的能量损耗。 当浪向角为 120°时, KVLCC2 的垂荡 RAO 在短波范围内 随着波长的增加而快速增大, 当 λ/L>1 时, 垂荡 RAO 曲 线趋于平缓, 波长的增大对垂荡运动的影响不大 。航速 Fn=0.055 的 RAO 曲线峰值比 Fn=0. 142 提前, 说明船舶与 波浪发生共振时的遭遇频率会随着航速的增大而提前 。 当浪向角为 90°, 即 KVLCC2船在横浪中航行时, 低航速 的垂荡运动响应高于高航速 。当 KVLCC2船在艉斜浪和 顺浪中航行时, 长波条件下两种航速的垂荡响应差距不 大, 说明长波条件下航速对垂荡运动的影响不大 。短波 条件下低航速的垂荡运动响应高于高航速。
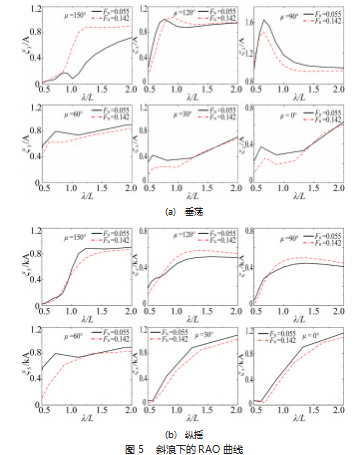
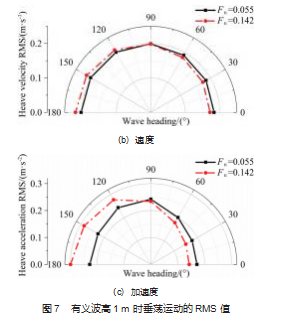
对于纵摇运动, 两种航速在不同浪向角下的 RAO 随 波长变化规律基本一致 。 当浪向角为 120°和 90°时, 高 航速的纵摇响应高于低航速; 其余浪向角下低航速的纵 摇运动响应要略高于高航速。
3.2 附加阻力
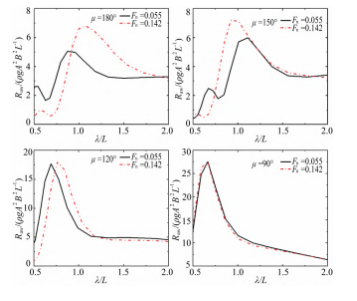
图 6 所示为两种航速下不同浪向角对应的波浪附加 阻力 (波浪增阻)。 无论是高航速还是低航速, KVLCC2 船的附加阻力随波长的变化规律是一致的: 随着波长的 增大, 附加阻力先增大后减小, 在部分艏斜浪的长波中, 附加阻力还会保持相对不变 。实际上, 附加阻力的大小 和随波长的变化规律是由船舶垂荡-纵摇的耦合运动所 决定的 。一般情况下当垂荡和纵摇 RAO 出现峰值时, 附 加阻力也会相应地出现峰值 。浪向角 180°和 150°的附加 阻力大小相差不大, 浪向角从 150°减小到 90°, 附加阻 力迅速增大, 在横浪状态达到最大 。而后随着浪向角的 继续减小, 附加阻力又会随之降低 。 总的来说, KV ‐ LCC2 在迎浪状态下航行时, 受到的附加阻力最小; 在横 浪中航行时附加阻力最大。
当浪向角为 180°时, 高航速在短波范围的附加阻力 小于低航速, 在中长波范围的附加阻力大于低航速, 随 着浪向角的减小, 长波条件下两种航速的附加阻力差距 逐渐缩小, 同时船舶与波浪的共振频率移动到了短波范 围 。横浪时两种航速的附加阻力曲线几乎重合 。当浪向 角小于 90°时, 低航速的附加阻力始终高于高航速 。 由 此可见: 当船舶在迎浪和艏斜浪中航行时, 降低航速可 以有效地减小附加阻力; 而当船舶在艉斜浪中航行时, 适当增大航速可以一定程度上减小附加阻力。
3.3 运动响应
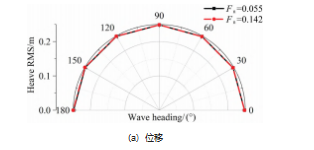
即 RMS 值为响应有义值的1/2 。图 7 所示为垂荡运动的位 移 、速度和加速度的 RMS 值 。图 8 所示为纵摇运动的角 度 、角速度和角加速度的 RMS 值 。加速度 (角加速度) 决定着速度 (角速度), 速度 (角速度) 又决定着位移 (角度)。 因此 3 种物理量在极坐标图中的曲线分布是一 致的, 而且从加速度到速度到位移, 航速的影响应该是 减弱的。
由图 7 可知, 有义波高 1 m 时航速和浪向角对垂荡位 移的影响不大, 两种航速在不同浪向角下的垂荡 RMS 值 基本一致 。迎浪条件下垂荡速度和加速度的 RMS 值最 大, 随着浪向角的减小, RMS 值略微减小 。艏斜浪中 (浪向角大于 90°且小于 180°) 高航速的速度和加速度 RMS 值高于低航速, 艉斜浪 (浪向角大于 0°且小于 90°)则相反 。 由图 8 可知, 纵摇运动的角度 RMS 值受浪向角 的影响强于航速 。纵摇运动的 RMS 曲线呈现 “M”状, 在浪向角为 0°和 180°下, 纵摇运动的 RMS 值相对较大, 在浪向角 90°下 RMS 值最小 。这说明 0°和 180°浪向角下 船体的纵摇运动最剧烈。
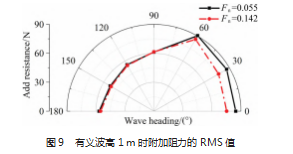
图 9 所示为有义波高 1 m 时 KVLCC2 的附加阻力RMS 值 。 由图可知, 当浪向角大于 90°时, 两种航速的附加 阻力 RMS 值基本一致; 当浪向角小于 90°, 低航速的附 加阻力高于高航速 。两种航速的附加阻力峰值均发生在 60°的浪向角下, 且船舶在艉斜浪中的附加阻力普遍高于 艏斜浪 。 由此可知, 为减小附加阻力所损耗的能量, 船 舶应尽量避免在艉斜浪中航行。
4 结束语
本文以 KVLCC2船模为研究对象, 利用切片理论, 研 究船模在斜浪中的运动响应和附加阻力, 得到结论如下。
( 1 ) 基于切片理论的计算值与实验值总体上吻合良 好 。在波长小于船长的短波条件下, 垂荡计算值与实验 相差较大, 当波长大于船长时, 垂荡计算值与实验值比 较接近 。纵摇运动的计算曲线总体上没有出现与实验值 偏差较大的部位。
( 2 ) 当波长大于船长时, 航速的改变带来了垂荡响 应的显著改变 。相同波长下高航速的垂荡响应明显大于 低速, 这意味着船舶需要提供更多的能量来克服垂荡运 动所引起的能量损耗 。当 KVLCC2船在艉斜浪和顺浪中 航行时, 长波条件下两种航速的垂荡响应差距不大, 说 明长波条件下航速对垂荡运动的影响不大 。短波条件下 低航速的垂荡运动响应高于高航速。
( 3 ) 当船舶在迎浪和艏斜浪中航行时, 降低航速可 以有效地减小附加阻力; 而当船舶在艉斜浪中航行时, 适当增大航速可以一定程度上减小附加阻力。
参考文献:
[1] 张宏绪, 张新曙, 黄昊,等 . 豪华邮轮耐波性及救生艇砰击载荷 特性研究[J/OL]. 海洋工程 ,2023(8):1- 15[2023-08-20]. https:// www.cnki.com.cn/Article/CJFDTotal-HYGC20230615005.htm.
[2] 毕效笙,马潇健,王大鹏,等 . 变结构滑行艇斜浪航行耐波性数 值分析[J]. 数字海洋与水下攻防,2023.6(3):286-292.
[3] 袁小平 . 基于 Rankine 源函数的船舶兴波阻力计算[J]. 舰船科学技术,2023.45(11):51-54.
[4] 刘树魁 . 波浪增阻预报的研究现状与未来展望[J]. 船舶,2023. 34(3):1-24.
[5] 张大朋,严谨,赵博文,等 .Maxsurf Motions 模块在船舶耐波性上 的应用与验证[J]. 科学技术与工程,2023.23(4):1734- 1746.
[6] 杨云涛,朱仁传, 陆安,等 . 基于频域高阶 Rankine 源法的有航速 船舶斜浪中六自由度运动数值计算研究[J]. 船舶力学,2022.26 (11):1668- 1679.
[7] 刘李为,余嘉威,冯大奎,等 . 艉斜浪下船舶倾覆特性直接 CFD 数值模拟[J]. 中国舰船研究,2022. 17(3):78-84.
[8] 仲亚 . 高速翼滑艇波浪增阻及运动响应特性研究[D]. 镇江:江 苏科技大学,2022.
[9] 任航 . 基于源汇分布法的船舶垂荡纵摇运动建模研究[D]. 大 连:大连海事大学,2021.
[10] 吴斌 . 基于切片理论冰间航道内船舶三维水动力计算方法 研究[D]. 镇江:江苏科技大学, 2022.
[11] 方昭昭 . 数值波浪水池中船舶辐射绕射的数值模拟[D]. 上 海:上海交通大学, 2011.
[12] 吕向琪, 张志恒, 张新曙,等 . 基于频域 Rankine 面元法的船 舶耐波性计算和分析[J]. 海洋工程, 2023. 41(1): 68-81.
[13] 周文俊, 徐萍, 周华伟,等 . 基于多层面改进多域法的航行船 舶时域水动力分析[J]. 船舶力学, 2023. 27(4): 481-497.
[14] 朱仁传, 徐德康, 王慧,等 . 船舶耐波性近期研究进展与若干 评述[J]. 船舶, 2022. 33(3): 1- 19.
[15] 刘亚柳,刘利琴,黄郑鑫 . 随机斜浪中船舶横摇-纵摇-升沉耦 合运动响应解析方法研究[C]//第三十一届全国水动力学研 讨会论文集(下册),2020:797-805.
[16] 王晋楷 , 万德成 . 基于 Lewis 剖面法快速评估船舶纵向运动 [J]. 中国造船,2020.61(1):60-68.
[17] 杨云涛 . 航行船舶运动的三维频域高阶面元法数值计算研 究[D]. 上海:上海交通大学,2020.
[18] 朱仁传, 缪国平 . 船舶在波浪上的运动理论[M]. 上海:上海交 通大学出版社, 2019.
[19] 王清 . 浅水对 KVLCC2 快速性及操纵性影响的数值模拟研 究[D]. 武汉:华中科技大学,2022.
[20] Wang Zhanzhi, Min Shaosong, Peng Fei. Numerical Study on Scale Effect of Form Factor for DTMB5415. KCS,KVLCC2. and 4000TEU Container Ship[J]. China Ocean Engineering, 2021. 35 (5):767-778.
[21] Seo Min Guk, Ha Yoon Jin, Nam Bo Woo. Experimental and Nu ‐ merical Analysis of Wave Drift Force on KVLCC2 Moving in Oblique Waves[J]. Journal of Marine Science and Engineering, 2021.9(2).
作者简介:
赵博文 ( 1998— ), 男, 山东济南人, 博士, 研究领域为计算 流体力学, 已发表论文 4 篇。
张大朋 ( 1987— ), 男, 山东聊城人, 博士, 讲师, 研究领域 为船舶与海洋结构物动态响应, 已发表论文 50 篇。
严 谨 ( 1978— ), 男, 陕西宝鸡人, 博士, 教授, 研究领域 为海洋工程结构动力分析, 已发表论文 60 篇。
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/64936.html