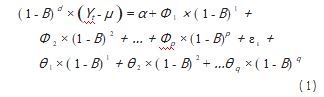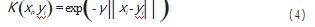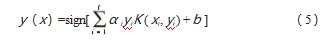基于 ARIMA 和 LS-SVM 组合模型的短期风速预测* 论文

SCI论文（www.lunwensci.com）

　　摘要：为了解决电力短期风速预测中存在的周期规律性误差序列问题， 提出了一种改进的 ARIMA-LS-SVM 组合模型。首先分析了 电力短期风速预测中的周期规律性误差序列问题， 并确定了 ARIMA 模型作为基础模型。然后， 引入最小二乘支持向量机 (LS- SVM) 来修正 ARIMA 模型的预测误差。 LS-SVM 是一种非线性回归方法， 通过将样本数据映射到高维特征空间， 构建一个最优超 平面来实现预测。通过对 ARIMA 模型的预测误差进行修正， 可以更准确地预测电力短期风速。采用北京某地风速数据进行实验验 证， 结果表明， 改进的 ARIMA-LS-SVM 组合模型在对北京某地风速进行预测时表现出了良好的预测精度和推广性。与传统的ARI⁃ MA 模型相比， 改进模型在各项评价指标上均取得了显著提高， 验证了该方法的有效性和实用性。提出的改进模型克服了周期规律 性误差序列对预测精度的影响， 为电力负荷预测和风速预测等相关领域提供了一种有效的预测方法。

　　Abstract: In order to solve the problem of periodic error sequences in short-term wind speed prediction of electricity, an improved ARIMA- LS-SVM combination model is proposed. Firstly, the periodic error sequence problem in short-term wind speed prediction of electricity is analyzed, and the ARIMA model is determined as the basic model. Then, the least squares support vector machine (LS-SVM) is introduced to correct the prediction error of the ARIMA model. LS-SVM is a nonlinear regression method, which realizes prediction by mapping sample data to high-dimensional feature space and constructing an optimal hyperplane . By correcting the prediction error of the ARIMA model, short-term wind speeds of electricity can be more accurately predicted . The experimental verification is conducted using wind speed data from a certain location in Beijing, and the results show that the improved ARIMA-LS-SVM composite model has good prediction accuracy and generalization in predicting wind speed. Compared with the traditional ARIMA model, the improved model has achieved significant improvements in all evaluation indicators, verifying the effectiveness and practicality of this method . The proposed improved model overcomes the impact of periodic error sequences on prediction accuracy and provides an effective prediction method for related fields such as power load prediction and wind speed prediction.

　　Key words: short-term wind speed prediction; ARIMA model; LS-SVM model; ARIMA-LS-SVM composite model; error correction

　　0 引言

　　随着可再生能源的快速发展， 风能成为一种重要的 清洁能源资源。然而， 风力发电的效率和稳定性很大程 度上依赖于准确的风速预测。准确地预测风速有助于风 力发电厂优化能源管理、提高发电效率以及有效应对风 能波动带来的挑战。

　　传统的风速预测方法通常采用统计方法和机器学习 方法。统计方法包括时间序列分析方法， 如 ARMA 模 型[1] 、ARIMA 模 型[2] 、指 数 平 滑 方 法[3] 、 回 归 分 析[4] 和 Kalman 滤波法[5] 等。这些方法通过对历史风速数据进行 统计和分析， 建立模型来预测未来的风速变化趋势。机器学习方法包括支持向量机 (SVM) [6]、人工神经网络 ( ANN ) [7]、随机森林 (Random Forest) [8]、长短期记忆 网 络[9] 、梯 度 提 升 树[10] 、 K 近 邻 回 归[11] 、 高 斯 过 程 回 归[12]、基于决策树的回归[13] 等。这些方法通过对大量的 历史数据进行学习和训练， 构建模型来预测未来的风速。 其中 ARIMA (自回归综合移动平均模型) 和 LS-SVM (Least Squares Support Vector Machines) [14] 被广泛应用于 时间序列数据的建模和预测。 ARIMA 模型通过对时间序 列数据的自回归和移动平均部分进行建模， 可以捕捉数 据的趋势和周期性。 LS-SVM 模型则基于 SVM 理论[15]， 通过非线性映射将数据映射到高维空间[16]， 并寻找一个最优超平面来拟合数据。

　　然而， 单独使用 ARIMA 或 LS-SVM 模型在风速预测 中存在一定的局限性。 ARIMA 模型往往无法很好地处理 非线性和非平稳的时间序列数据， 而 LS-SVM 模型可能 会受到高维特征空间的维度灾难问题的影响。为了克服 这些限制并提高风速预测的准确性， 提出了一种基于 ARIMA 和 LS-SVM 组合模型的短期风速预测方法。

　　本文介绍了 ARIMA 和 LS-SVM 模型的原理和方法， 并详细描述基于 ARIMA 和 LS-SVM 组合模型的短期风速 预测框架。使用实际的风速数据集进行实证分析， 并对 预测结果进行评估和分析。通过本文的研究成果， 期望 能为风力发电行业提供一种可行的方法，以改进风速预测 的准确性和可靠性， 从而提高风力发电的效率和稳定性。

　　1 ARIMA 模型

　　ARIMA (Autoregressive Integrated Moving Average) 是一种常用于时间序列分析和预测的统计模型。它的基 本思想是将一个非平稳时间序列转化为一个平稳时间序 列， 然后对这个平稳时间序列进行建模和预测。

　　ARIMA 模 型 包 括 3 个 部 分： 自 回 归 (AR)、 差 分 ( I)、移动平均 (MA)。

　　自回归 (AR) 部分表示当前值受过去一段时间内自 身的影响， 即当前值与前p个时间点的值之间存在线性 关系， 这个部分用p 阶自回归系数来表示。

　　差分 (I) 部分是为了将非平稳时间序列转化为平稳 时间序列， 通常采用差分的方式， 即将时间序列逐阶 差分， 直到得到平稳时间序列。这个部分用 d 阶差分 来表示。

　　移动平均 (MA) 部分表示当前值受过去一段时间内 噪声的影响， 即当前值与前 q个时间点的噪声之间存在 线性关系， 这个部分用 q 阶移动平均系数来表示。

　　将 3 个部分合并起来， 得到 ARIMA (p， d， q) 模 型， 其中p 表示自回归部分的阶数， d 表示差分部分的 阶数， q 表示移动平均部分的阶数。它的表达式可以写成：

　　式中： Yt 为原始时间序列; μ 为该序列的均值; α 为常数 项; εt 为一个均值为 0、方差为 σ2 的白噪声; Φ i、θj 为待 估参数。

　　ARIMA 模型可以用来进行时间序列的预测和模拟。 当使用符号表示时间序列模型时， 通常需要使用下标来 表示时间点， 以便明确每个值所对应的时间。在 ARIMA模型中， 时间序列的观测值用 Yt 表示， 其中 t 是时间点的下标。下面是 ARIMA 模型中各个部分的具体解释。

　　(1 - B )d × (Yt - μ )： 表示对时间序列进行 d 阶差分 后， 再减去均值 μ 的结果。其中， d 表示差分的阶数，(1 - B )d 表示进行 d 次差分的操作符， Yt - μ 表示减去均 值后的时间序列。

　　α： 表示模型中的常数项或截距， 它是一个待估参数。

　　Φ 1 ×(1 - B) 1 + Φ 2 ×(1 - B) 2 +…+Φp × (1 - B)p： 表示 自回归项， 其中 Φi 是自回归系数， p 是自回归项的阶数， ( 1 - B) i 表示对时间序列进行 i 阶滞后操作的操作符。

　　εt： 表示时间序列的随机误差或扰动项， 它是一个 正态分布的白噪声过程， 均值为 0. 方差为常数 σ2.

　　θ 1 × (1 - B) 1 +θ2 × (1 - B) 2 +…+θq × (1 - B) q： 表 示 移动平均项， 其中 θj 是移动平均系数， q 是移动平均项的 阶数， ( 1 - B) i 表示对随机误差进行 i 阶滞后操作的操 作符。

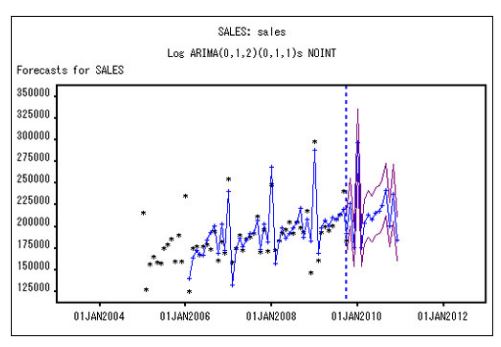
　　利用 ARIMA 模型预测北京某地 2023 年 3 月 11 日 11 时至 2023 年 4 月 10 日 11 时每 3 h 的实际风速值、大气压 和气温情况。首先对数据进行初步处理， 比如对风速值 进行周期性差分和一阶有序差分变换， 以使得序列平稳。

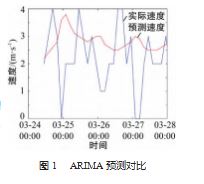
　　然后根据时间序列的自相关函数和偏自相关函数 来 定 阶 和 估 计 参 数，得出 ARIMA ( 2. 1. 1 )模型， 根据该模型进行预测， 得到未来每 3 h 的风速值， 2023 年 3 月 24日 11 时到 2023 年 3 月28日 2 时的预测对比如图 1 图 1 ARIMA 预测对比所示。

　　ARIMA 模型的预测误差序列存在随机波动性， 但是 其中仍然存在明显的周期规律性， 说明其中仍然有可利 用的信息。然而， ARIMA 模型仅仅考虑了时间因素， 无 法考虑其他因素如气压和温度等因素对风速的影响， 因 此其预测精度存在限制。为了改善 ARIMA 模型的预测精 度， 可以利用 LS-SVM 提取 ARIMA 预测偏差中的敏感分 量。具体而言， LS-SVM 是一种基于支持向量机的非线 性回归方法， 它可以通过构建一个非线性映射将原始数 据映射到一个高维空间中， 从而提高模型的拟合能力。 利用 LS-SVM 可以将 ARIMA 模型预测偏差中的敏感分量 提取出来， 然后将其纳入模型中， 从而改善 ARIMA 模型 的预测精度。

　　2 LS-SVM 偏差修正模型建立

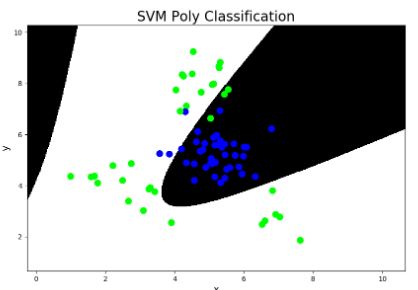
　　对于有限样本的学习， 通常使用经验风险最小化原则来训练模型。也就是说， 在训练数据上尽量减小训练 误差。然而， 当训练误差过低时， 可能会导致模型的泛 化能力下降， 即模型对未知数据的预测准确率会变低。 为了解决这个问题， SVM 算法应运而生。它以统计学习 理论为基础， 专门针对有限样本。 SVM 算法与其他算法 不同之处在于， 它的设计不仅仅是为了最小化训练误差， 而是为了最大化间隔 (margin)。这样能够提高算法的泛 化能力， 并且减少过拟合的风险。更具体地说， SVM 算 法的优化目标是最大化支持向量到分类超平面的距离， 也就是最大化间隔。这样做能够有效地提高算法的泛化 能力， 因为它能够更好地适应未知数据。

　　假设有一组偏差训练样本， 其中每个样本由一个输 入向量 xi 和对应的目标输出值 yi 组成。由于样本呈现出 非线性的关系， 因此需要将每个样本点通过非线性函数 Φ 映射到高维特征空间， 然后在高维特征空间中进行线 性回归来实现在原空间中的非线性回归效果。这样， 就 能够更好地拟合数据， 并且提高模型的预测准确率。

　　LS-SVM 是一种用于回归分析的机器学习算法， 其 核心思想是将输入样本映射到高维空间中， 并利用支持 向量机 (SVM) 的方法来求解回归函数。在 LS-SVM 中， 回归函数的形式为：

　　式中： w 为权重向量; Φ(x )为非线性函数对输入向量 x 的映射; b 为偏置项。

　　LS-SVM 的目标是学习一个最优的回归函数， 使得 模型在训练集上的误差最小化， 并能够在未知数据上进 行准确预测。

　　为了在保证训练误差最小化的同时最小化模型的泛 化误差， LS-SVM 采用了结构风险最小化原则来确定回 归函数。与经验风险最小化相比， 结构风险最小化引入 了正则化项来限制模型的复杂度， 避免过拟合现象的发 生。过拟合是指模型在训练集上表现良好， 但在测试集 上却表现不佳的现象， 通常是由于模型过于复杂而导致的。

　　SRM 中的正则化项可以看作是一个约束条件， 通过 对模型参数进行约束， 使得模型的复杂度受到限制， 从 而增强了模型的泛化能力。这样， 在保证训练误差最小 化的前提下， LS-SVM 可以更加准确地预测新的数据点 的输出值。

　　为了简化计算过程并提高算法效率， LS-SVM 采用 了最小二乘法来进行模型参数求解。总之， LS-SVM 通 过结构风险最小化原则来确定回归函数， 旨在保证训练 误差最小化的同时尽可能减少模型的泛化误差， 提高模 型的预测准确性。正则化项的引入有效限制了模型的复 杂度， 避免了过拟合现象的发生， 提高了 LS-SVM 的泛 化能力。

　　LS-SVM 算法是一种用于回归分析的机器学习算法， 它基于 SVM 算法， 并将支持向量机的思想应用到回归问 题中。与传统的回归方法不同， LS-SVM通过将输入样本映 射到高维特征空间中， 实现在原空间中的非线性回归效果。

　　具体来说， 假设有一组包含训练样本的数据集， 其 中每个样本由一个输入向量 xi 和对应的目标输出值 yi 组 成。由于样本呈现出非线性的关系， 因此需要将每个样 本点通过非线性函数 Φ 映射到高维特征空间， 然后在高 维特征空间中进行线性回归来实现在原空间中的非线性 回归效果。

　　LS-SVM 的优化目标是最小化以下式子：

　　式中： ω 为权值系数; b 为常值偏差; C 为惩罚系数; ϵ i 为松弛因子。

　　为了解决过拟合问题， LS-SVM 采用结构风险最小 化原则来确定回归函数。与经验风险最小化相比， 结构 风险最小化引入了正则化项来限制模型的复杂度， 避免 过拟合现象的发生。过拟合是指模型在训练集上表现良 好， 但在测试集上却表现不佳的现象， 通常是由于模型 过于复杂而导致的。

　　LS-SVM 中的正则化项可以看做是一个约束条件， 通过对模型参数进行约束， 使得模型的复杂度受到限制， 从而增强了模型的泛化能力。这样， 在保证训练误差最 小化的前提下， LS-SVM 可以更加准确地预测新的数据 点的输出值。

　　为了简化计算过程并提高算法效率， LS-SVM 采用 了最小二乘法来进行模型参数求解。具体来说， LS- SVM 通过求解拉格朗日函数实现对权重向量、偏置项和 松弛因子的求解， 并且使用核函数代替内积操作， 进一 步提高了算法的效率。其中， 径向基函数 (RBF) 是一 种常用的核函数。 RBF 核函数的形式为：

　　在 RBF 核函数中， 指数函数 exp 的作用是将输入样 本映射到高维空间中， 并且使得距离较远的数据点在新 的特征空间中距离更远。通过选择不同的参数 γ， 可以 调整映射后的数据点在特征空间中的分布情况， 从而获 得更好的分类效果。

　　因此， 最小二乘支持向量机的决策函数可以表示为：

　　通过选择不同的核函数和调整超参数 C 和 γ， 可以 获得更好的回归效果。

　　3 算例分析

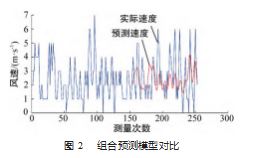
　　利用 LS-SVM 模型对北京某地风速 ARIMA 预测偏 差进行修正。 LS-SVM 中使用径向基函数 (RBF) 作为 核函数， 并且使用交叉验证来确定将核函数参数 σ 设置 为 5. C 设置为 0.05.最终将 LS-SVM 得到的残差预测值 加回到 ARIMA 模型的预测值中， 得到最终的预测值， 并且画出预测结果的图像。 2023 年 4 月 3 日 11 时开始 到 2023 年 4 月 4 日 11 时的预测风速和实际风速如图 2 所示。

　　ARIMA 和组合预测模型的预测值及预测误差如图 3 所示。

　　均方误差 (MSE) 和平均绝对误差 (MAE) 是用来 评估预测模型的精度的两个常用指标。其中， MSE 表示 预测值与真实值之间差值的平方和的平均值， 可以用下 式计算：

　　式中： n 为样本数量; yi 为第 i 个样本的真实值; ŷ i 为第 i 个样本的预测值。

　　MAE 则表示预测值与真实值之间差值的绝对值的平 均值， 可以用下式计算：

　　根据给出的表格， 可以计算出 ARIMA 和 ARIMA- LS-SVM 组合模型在这个结果中的 MSE 和 MAE。

　　对于 ARIMA 模型， 将其预测误差的平方和求均值即 可得到 MSE; 将其预测误差的绝对值求平均即可得到 MAE。同样的， 对于 ARIMA-LS-SVM 组合模型， 也可 以用类似的方法计算出 MSE 和 MAE。

　　下面是计算结果：

　　ARIMA 模型： MSE = ( 0.387 882+1.615 32+0.616 582+ 0.379 432 + 0.203 522 + 3. 117 12 + 3.039 82 + 1. 161 62 ) / 8 ≈ 3. 162 4;MAE = ( 0.387 88 + 1.615 3 + 0.616 58 + 0.379 43 + 0.203 52 + 3. 117 1 + 3.039 8 + 1. 161 6 ) / 8 ≈ 1.606 9.ARIMA-LS-SVM 组 合 模 型： MSE = ( 0.078 092 + 1.029 22 + 0.326 512 + 0.222 472 + 0.991 992 + 0.324 642 + 0.178 822 + 0.082 8752 ) / 8 ≈ 0.579 1 ;MAE = ( 0.078 09 + 1.029 2 + 0.326 51 + 0.222 47 + 0.991 99 + 0.324 64 + 0. 178 82 + 0.082 875 ) / 8 ≈ 0.523 6.

　　因 此， 在 这 个 结 果 中， ARIMA 模 型 的 MSE 约 为 3.162 4. MAE 约为 1.606 9; 而 ARIMA-LS-SVM 组合模 型的 MSE 约为 0.579 1. MAE 约为 0.523 6.

　　由预测结果可知： 虽然 ARIMA 的预测精度比较理 想， 但 ARIMA-LS-SVM 能在 ARIMA 的基础上进一步提 高预测精度， 其中 eMAPE 降低了 0.67%; eRMSE 减小 了 7.48 MW。即平均每个时刻点的绝对误差显著减小， 这对于复杂的电力短期风速预测来说是较大的进步。

　　4 结束语

　　经过对短期风速预测方法的比较研究， 本文发现 ARIMA-LS-SVM 在准确性和精度方面优于传统的 ARI⁃ MA 模型。 ARIMA-LS-SVM 在 ARIMA 的基础上引入支持 向量机进行进一步的预测优化， 有效地减少了每个时刻 点的绝对误差。这一发现对电力短期风速预测具有重要 意义， 并标志着该领域的一项重要进展。

　　随着数据科学和人工智能技术的快速发展， 可以期 待未来更加高效、准确的电力短期风速预测模型的出现。 未来的研究可能会探索其他混合模型， 如深度学习[17]， 集成学习方法[18- 19]， 时间序列分解方法[20] 等方法， 以进 一步提高短期风速预测的精度和可靠性。深度学习模型 能够从大规模数据中学习复杂的非线性关系， 有望在风 速预测中发挥重要作用。集成学习是通过组合多个模型 来提高预测性能的技术。可以考虑使用 Bagging 、Boost⁃ing 或 Stacking 等集成学习方法， 将 ARIMA-LS-SVM 与其 他模型进行组合， 以进一步提升预测准确性。 ARIMA- LS-SVM 模型可以通过分解时间序列为趋势、季节性和 残差等组成部分， 然后对每个部分分别建模。

　　本文的创新点在于引入支持向量机优化 ARIMA 模 型， 提高了短期风速预测的准确性和精度。通过综合考 虑时间序列分析和机器学习的优势， ARIMA-LS-SVM 模 型克服了 ARIMA 模型在非线性问题上的不足， 提高了预 测性能。这一创新对于改进电力短期风速预测方法具有 重要的实际应用价值。

　　电力短期风速预测在可再生能源领域具有重要的应 用前景。精确预测风速可以帮助电力系统管理者优化风 力发电的计划和调度， 提高电力系统的稳定性和可靠性。

　　因此， 研究者们将继续致力于提高风速预测的精度和可 靠性。未来的研究可以进一步探索其他预测模型、算法 和数据特征， 以获得更准确、可靠的预测结果。

　　总之， 本文通过比较分析 ARIMA-LS-SVM 和 ARI⁃ MA 模型在短期风速预测中的表现， 揭示了ARIMA-LS- SVM 模型在准确性和精度方面的优势， 并探讨了未来可 能的研究方向。这些研究结果对于提高电力短期风速预 测的效果以及可再生能源的可持续发展具有重要的指导 意义。本文的创新内容在于引入支持向量机优化 ARIMA 模型， 为相关领域的研究和实践提供了有价值的参考。

　　参考文献：

　　[1] 胡林静,付燕杰, 郭洒洒 . 基于时间序列的 ARMA 风速预测模 型的建立与分析[C]//中国高科技产业化研究会智能信息处理 产业化分会第九届全国信号和智能信息处理与应用学术会 议,2015:293-297.
　　[2] 张冬雪 . 基于 LSTM 和 ARIMA 的风速时间序列预测研究[D]. 兰州: 兰州大学,2020.
　　[3] 齐雪雯,徐玉韬 . 基于指数平滑方法的风速分布预测[J]. 贵州 电力技术,2016.19(11):18-23.
　　[4] 徐群 . 非线性回归分析的方法研究[D]. 合肥 :合肥工业大学 , 2009.
　　[5] 许国辉,徐晖 . 卡尔曼滤波法方差估计的理论研究[J]. 武汉大 学学报(工学版),2004(4):28-31.
　　[6] 罗默涵 . 基于优化支持向量机方法的风电场风速预测研究[J]. 机电信息,2021(26):6-7.
　　[7] 陈水明 . 基于改进 BP 神经网络的风电功率预测[J]. 中国高新 科技,2023(7):30-32.
　　[8] 付旭东,王金艳,李龙燕,等 . 基于随机森林算法的风场预报[J]. 兰州大学学报(自然科学版),2021.57(4):503-509.
　　[9] 魏昱洲,许西宁 . 基于 LSTM 长短期记忆网络的超短期风速预 测[J]. 电子测量与仪器学报,2019.33(2):64-71.
　　[10] 孙川永, 彭友兵,刘志亮,等 . 梯度提升树算法在陕北风电场短 期风电功率预测中的应用[J]. 电网与清洁能源 ,2022.38(4): 124- 128.
　　[11] 翟宇梅,赵瑞星, 肖仁春,等 .K 近邻非参数回归概率预报技术 及其应用[J]. 应用气象学报,2005(4):453-460.
　　[12] 孙斌,姚海涛,刘婷 . 基于高斯过程回归的短期风速预测[J]. 中 国电机工程学报,2012.32(29):104- 109.
　　[13] 伊卫国 . 基于关联规则与决策树的预测方法研究及其应用 [D]. 大连: 大连海事大学,2012.
　　[14] 范曼萍, 周冬 . 基于改进粒子群优化 LS-SVM 的短期风速预 测[J]. 电力学报,2020.35(2):123- 128.
　　[15] 丁世飞, 齐丙娟,谭红艳 . 支持向量机理论与算法研究综述[J]. 电子科技大学学报,2011.40(1):2- 10.
　　[16] 刘卓 . 高维数据分析中的降维方法研究[D]. 长沙 : 中国人民 解放军国防科学技术大学,2002.
　　[17] 刘擘龙, 张宏立,王聪,等 . 基于序列到序列和注意力机制的超 短期风速预测[J]. 太阳能学报,2021.42(9):286-294.
　　[18] 徐继伟,杨云 . 集成学习方法 :研究综述[J]. 云南大学学报(自 然科学版),2018.40(6):1082- 1092.
　　[19] 鲍海波, 吴阳晨, 张国应,等 . 基于特征加权 Stacking 集成学习 的净负荷预测方法[J]. 电力建设,2022.43(9):104- 116.
　　[20] 李德顺,李宁,李银然,等 . 基于小波分解的 DIF-RBFNN 超短期 风速组合预测方法[J]. 兰州理工大学学报,2019.45(4):63-66.
 
关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/64874.html