形位公差对小模数直齿轮传动系统精度的影响论文

SCI论文（www.lunwensci.com）　　

　　摘要：形位公差是零件形状和位置特征变动的结果，形位特征的变动对于精密传动的传动精度产生很大影响。目前在小模数直齿轮传动系统精度计算中仅考虑齿轮副尺寸公差、齿轮副扭转弹性空回程、温度变化引起的圆周侧隙等，没有考虑形位公差的影响。本文以小模数直齿轮传动系统为研究对象，研究箱体形位公差对传动精度的影响。通过分析箱体的平行度、同轴度、垂直度等形位公差的定义，得出平行度、垂直度对中心距的影响，提出在独立原则下的小模数齿轮传动精度的计算方法，为计算小模数齿轮传动精度提供思路。最后通过一个工程应用实例，说明提出计算方法的必要性。

　　关键词：小模数直齿轮；传动系统；传动精度；形位公差

　　Abstract:Space and place error is the result of the change of parts'space and place characteristics,and the change of space and place characteristics has a great influence on the transmission accuracy of precision transmission.At present,in the accuracy calculation of fine-pitch spur gears transmission system,only the dimensional tolerance of gear pair,the torsional elastic backlash of gear pair,and the circumferential backlash caused by temperature change are considered,and the influence of form and space and place error is not considered.Taking fine-pitch spur gears transmission system as the object,the influence of box space and place error on transmission accuracy is studied.By analyzing the definition of space and place error such as parallelism,coaxiality and perpendicularity of the box,the influence of space and place error on the center distance is obtained,and the calculation method of fine-pitch spur gear transmission accuracy under the principle of

　　independence is proposed,which provides ideas for calculating fine-pitch spur gears transmission accuracy.Finally,an engineering application example is given to illustrate the necessity of the proposed calculation method.

　　Key words:fine-pitch spur involute cylindrical gears;transmission system;transmission accuracy;space and place error

　　0引言

　　齿轮传动是应用非常广泛的一种机械传动，它具有传动精度高、传递功率范围宽、工作可靠、使用寿命长、传动效率高、可实现平行轴传动、交错轴传动等特点。齿轮传动有两种工作方式：一种用来传递力、力矩，如各种类型减速器；另一种传递运动，如测量仪器的齿轮传动、机床的分度齿轮传动、控制系统中的位置反馈机构等。齿轮的传动精度主要是指齿轮传动的准确性。由于齿轮传动装置的零部件(包括齿轮、轴、轴承等)存在制造误差和装配误差，以及在传动过程中还会产生温度变形和受力弹性变形等，因此在传动过程中输出轴的转角总会有误差存在。对于齿轮传动装置来说，这种误差主要是传动误差和空程[1]。

　　发射装置受信仪作为发射装置的位置反馈机构，一般通过小模数齿轮传动将设备到位角度反馈给控制设备。

　　由于系统要求，受信仪的传动精度较高，因此进行受信仪设计时有必要对传动精度预计。对于小模数直齿轮传动精度，国内进行了不少相关研究。文献[2-5]在研究过程中，考虑了齿轮孔与轴配合误差、轴承跳动误差、齿轮制造误差引起的传动误差、单个齿轮综合传动误差、输出轴的误差，但未考虑箱体形位公差对传动系统精度的影响。对于单个零件的形位公差对尺寸链的影响，国内学者对这一个课题进行了相关研究，文献[6-7]提出了考虑形位公差(如同轴度、垂直度)的装配尺寸链计算方法，并通过采用极值法计算得出考虑形位公差时最小配合间隙减小，装配精度也降低了。文献[8-9]提出了应用蒙特卡洛仿真法进行考虑形位公差的公差尺寸计算方法。文献[10]提出了一种新的关于矢量环装配模型的包括几乎所有形位特征变动的二维装配公差分析方法，并举例计算了含形位公差的顶柱装配，得出了考虑了形位公差及其影响，则封闭环的公差增加。综合文献[2-10]可以得出：在小模数齿轮齿轮传动系统中，设计时如果不考虑的箱体形位公差因素，得出的传动精度计算值是偏小的，如果设计的传动精度没有足够裕度，加工完成的小模数直齿轮传动机构就有可能出现传动精度不满足系统要求。

　　1小模数齿轮传动精度分析中考虑形位公差的条件形状公差为零件上的实际几何要素的形状与理想形

　　状之间的误差，位置公差为零件的实际几何位置与理想位置之间的误差，形状误差和位置误差简称为形位公差。GB/T 1182—2018将形位公差分为4类：形状公差、方向公差、位置公差和跳动公差。公差原则分为独立原则和相关原则，相关原则又可分为包容原则和最大实体原则[11]。根据零件尺寸及形位公差所采用的公差原则，传动精度分析中对形位公差的处理方法也有不同。

　　1.1按包容要求设计的零件

　　包容要求是被测实际要素处处不得超越最大实体边界的一种要求，采用包容要求的尺寸要素，应在其尺寸极限偏差或公差代号后加注符号“E”。包容要求的实质就是用零件的尺寸公差控制其形位公差，因此，在包容要求下，箱体的形位公差包含于尺寸公差内，不会对小模数齿轮的传动系统的精度产生影响，因此进行传动精度计算时，只需考虑齿轮误差、齿轮与轴装配误差等，不需要计入箱体的形位公差。

　　1.2按独立原则设计的零件

　　图样上给出的每个尺寸要求和几何(形状、方向或位置)要求之间均相互独立，应各自满足要求。产品图样的实际规范中提出：没有规定有其他标准或特殊标注的，就表示遵守独立原则。在独立原则下，实际要素的尺寸由尺寸公差控制，与形位公差无关；形位公差由形位公差控制，与尺寸公差无关。因此，在计算传动精度时，除考虑齿轮等尺寸公差外，还应考虑相应的形位公差。

　　2小模数齿轮传动系统误差

　　2.1齿轮传动系统误差

　　齿轮传动误差概念由英国剑桥大学教授Smith于20世纪70年代提出：“在驱动为完全准确且为刚性的条件下，输出齿轮的理论位置与实际位置之间的差值”[12]。传动的综合传动误差由回差和传动误差组成。传动链的传动误差是各个齿轮传动误差的综合，而各个齿轮的传动误差主要是由齿轮的本身和所在的轴、轴承等零件制造、装配时的误差所引起的[13]。SJ 2557—1984小模数渐开线圆柱齿轮传动链精度计算方法提出了小模数渐开线圆柱齿轮传动链空程计算公式[14]，公式中考虑了齿轮副圆周侧隙引起的空程均值、齿轮副扭转弹性空回程、温度变化引起的圆周侧隙导致的空行程。因本文仅考虑因箱体加工因素导致的齿轮副圆周侧隙引起的空程均值进行分析，不对齿轮副扭转弹性空回程、温度变化引起的圆周侧隙造成变化。故在不考虑温度，扭转空行程弹性空行程的条件下，齿轮单向传动误差∆φ见式(1)，传动副传动回差∆φ'见式(2)，齿轮传动系统输出轴最大回程误差Φ见公式(6)。

　　2.2形位公差对小模数齿轮传动系统精度的影响

　　在小模数直齿轮传动系统设计中，零部件的设计一般采用独立原则，设计时为便于控制零件的加工精度及装配精度，通常在箱体设计图纸上标注轴系的平行度、同轴度及圆跳动等形位公差。由形位公差的定义可知：箱体的平行度、同轴度影响齿轮副装配时的中心距，齿轮箱的圆跳动影响齿轮的圆跳动。下面分别进行讨论分析。

　　2.2.1箱体平行度公差对齿轮传动中心距影响

　　箱体实际加工的轴孔可能出现轴线平行或轴线不平行两种情况。由形位公差定义可以得出：当两轴线平行时，平行度公差对中心距影响最大，因此平行度对中心距的影响以两轴线平行进行分析。设计中齿轮传动轴系有两种布置方式：(1)一维布置，齿轮副中的两个齿轮中心在水平方向(或高度方向)上横坐标有差值，纵坐标一致，或两个齿轮中心在高度方向(或水平方向)上纵坐标有差值，横坐标一致(图1)。(2)二维布置，齿轮副中的两个齿轮中心在水平方向(或高度方向)上横坐标均有差值(图2)。两种情况下，箱体平行度公差对中心距的影响分别进行讨论。

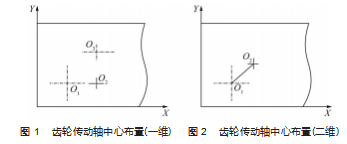
　　假设齿轮1在箱体上安装中心为O1，齿轮2安装中心为O2，齿轮3安装中心为O3。当齿轮副中心为在箱体上为一维布置时(图1)，箱体平行度公差对齿轮传动的中心距的影响为仅为增加或减少(图3)。由GB/T 1182—2018中有关定义可知：平行度公差为非对称环。因此按极值法分析时，计算时平行度公差的应取图纸上标注值IT。由图1可得出当齿轮轴中心为一维方向(X轴方向)时，平行度影响导致齿轮副中心距增加的公差最大值为：

　　由式(7)和式(10)可以看出，当ΔD2=0或ΔD2=0时，即齿轮轴中心布局由二维布置方式变为一维。所以无论齿轮轴中心布置方式为一维还是二维布置方式，均可以用式(10)进行计算因平行度导致中心距增加的公差。

　　2.2.2箱体同轴度公差对齿轮副中心距影响

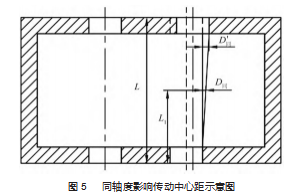
　　由同轴度的定义可以得知：箱体的同轴度将造成轴与箱体的平面不垂直，最终将影响传动系统的中心距。假设箱体宽度为L，齿轮安装处宽度为L1，则可得出箱体因同轴度影响传动中心距的示意图(图5)。同轴度公差为IT，由GB/T 1182—2018中有关定义可知：同轴度、园跳动为对称环，因此，在计算同轴度的对传动中心距的影响时，因取公差值的一半。由图5可得出：

　　ΔD'同=D同

　　式中：D同的数值取箱体轴承孔同轴度公差值的一半；L为箱体宽度；L1为齿轮安装处位置；ΔD'同为因箱体同轴度导致的安装中心距偏差。

　　2.2.3箱体轴孔圆跳动公差对齿轮副中心距影响

　　对于轴来说，箱体的圆跳动直接影响轴的圆跳动。其对于轴的跳动影响非常复杂，对于采用极值法分析来说，可以简单地认为对于传动中心距的影响为直接相加。由GB/T 1182—2018中有关定义可知：园跳动为对称环，因此，在计算圆跳动的对传动中心距的影响时，因取公差值的一半。因箱体圆跳动公差导致的径向圆跳动为：

　　3实例分析

　　小模数直齿轮传动系统通过模数为5、齿数为18的齿轮Z0与回转机构齿轮啮合，然后经过两级小模数直齿轮减速，最终齿轮Z4的转速与实际回转机构转速比为1∶1。机电编码器通过弹性联轴器与连接在轴Ⅲ上，当回转机构转动时，机电编码器实时将角度数据反馈给控制计算机。齿轮传动中心布置为一维方式，箱体孔平行度、圆跳动、同轴度公差均为6级。小模数直齿轮传动结构示意图如图6所示，传动参数表如表1。

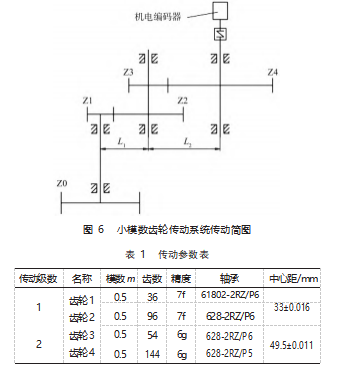
　　设计中，齿轮孔与轴配合公差分别选择H7/h6、H6/h5，轴中心距公差选7级精度，轴Ⅰ、轴Ⅱ、轴Ⅲ之间箱体宽度为100 mm，齿轮安装处距箱体内壁50，根据齿轮、轴承型号及精度等级，查机械设计手册及相关标准，齿轮、轴公差、圆跳动公差见表2，根据GB/T 1182—2018查出各个精度等级的平行度公差(表3)，根据GB 10095—1988可以查出不同精度等级下的传动中心距极限偏差(表4)。

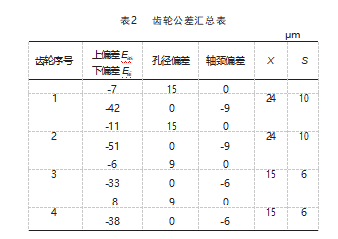
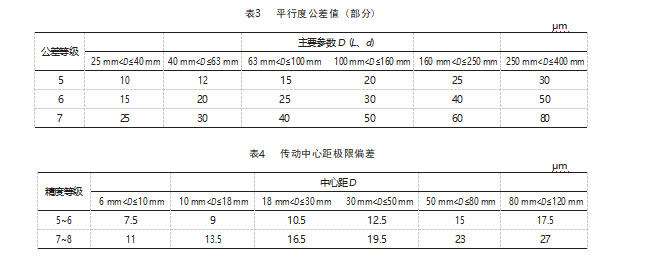
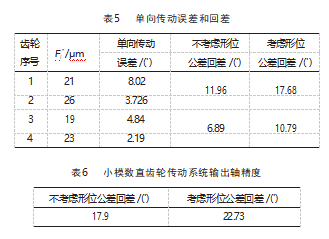
　　按照式(1)计算齿轮对单向传动误差见表5，按照式(3)和式(13)分别计算小模数齿轮副输出轴回差见表5，小模数齿轮传动系统传动精度计算如表6所示。表中数据表明：采用极值法进行小模数齿轮精度计算时，考虑箱体形位公差时得到的传动精度低于不考虑形位公差时的传动精度值。

　　4结束语

　　本文研究了箱体平行度误差、同轴度误差及圆跳动误差对直齿轮传动系统精度的影响，通过对形位公差要素所采用的公差原则分析，得出了在独立原则下箱体的平行度公差、同轴度公差将影响齿轮副的中心距，箱体圆跳动影响齿轮的圆跳动，提出了在独立原则下含形位公差的小模数齿轮传动精度的极值法计算公式。利用两种不同公式对同一个传动系统计算，计算结果相差大于20%。因此，在设计时如采用SJ 2557—1984中相关计算公式对传动精度进行预计，如计算出的传动精度值与设计要求相接近，最终设计时需要提高中心距、平行度、同轴度、圆跳动公差的精度等级，否则设计的传动系统最终传动精度可能无法满足要求。

　　参考文献：

　　[1]吴昭同,张鄂,蒋承蔚.齿轮精度标准与检验手册[M].北京:中国计量出版社,1994.

　　[2]李军,李润方,林超,等.小模数精密齿轮传动误差分析及实验研究[J].机械,2003(1):15-17.

　　[3]林长洪,朱家诚.齿轮传递误差计算的分析[J].机械,2011,38(8):10-13.

　　[4]庞茂,孔敏.盘式制动器总成形位公差在线测量机开发[J].机电工程,2021,38(12):1558-1563.

　　[5]张磊磊,范元勋.齿轮侧隙对齿轮传动精度的影响分析[J].机床与液压,2017,45(17):114-116.

　　[6]张炜.具有形位误差的装配尺寸链的分析计算[J].甘肃农业大学学报,1997(4):33-36.

　　[7]王凯军,陈飞.尺寸链计算中同轴度误差的处理方法[J].木工机床,2006(2):18-19.

　　[8]王太勇,熊越东,路世忠,等.蒙特卡洛仿真法在尺寸及公差设计中的应用[J].农业机械学报,2005(5):101-104.

　　[9]李仲辉,鲁世红.考虑形位公差的装配公差分析[J].机械工程与自动化,2010(3):105-107.

　　[10]彭和平,刘晓军.考虑形位公差的二维装配公差分析[J].机械传动,2008(3):75-77.

　　[11]甘永立,吕林森.新编公差原则与几何精度设计[M].北京:国防工业出版社,2007.

　　[12]SMITH J D.The uses and limitation of transmission error[J].Gear Technology,1988.

　　[13]徐峰,李庆祥.精密机械设计[M].北京:清华大学出版社,2005.

　　[14]SJ2557-1984,小模数渐开线圆柱齿轮传动链精度计算方法[S].

关注SCI论文创作发表，寻求SCI论文修改润色、SCI论文代发表等服务支撑，请锁定SCI论文网！

文章出自SCI论文网转载请注明出处：https://www.lunwensci.com/ligonglunwen/64861.html