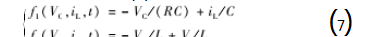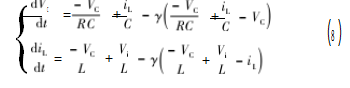SCI论文(www.lunwensci.com)
摘要:为进一步探索开关变换器的非线性特性和混沌控制方法,对电流断续导通工况下的BUCK 变换器进行了研究。通过MATLAB 建模仿真,分别研究了电流断续导通模式BUCK 变换器工作状态与输入电压Vi、电容C 和电感L 3 种电路参数的影响关系。在选定 条件下改变3种电路参数,均观察到了系统从单周期稳定态到倍周期分岔,再到混沌的演化过程。仿真结果表明3种电路参数对系 统状态的影响方式互不相同,且相较于电流连续导通模式,断续导通模式具有更复杂的变化规律。在此基础上采用一种混沌控制策 略,实现了对断续导通模式BUCK 变换器的混沌控制。该控制策略快速有效,仅需0.6 μs 就可以将系统从混沌态控制到稳定态。 此外,该控制策略不需要设定预期的目标轨道,不依赖变换器自身电路参数,仅需调整一个外部可调参数,在验证仿真模型正确的同时也提供了一种有效的混沌控制方法。
关键词:BUCK 变换器,断续导通模式,混沌控制
Modeling and Chaos Control of Buck Converter i DCM
Lu Yu,Gong Jian,Zhang Yan
( The 723 Institute of CSSC,Yangzhou,Jiangsu 225101.China )
Abstract:To further explore the nonlinear characteristic and the chaos control method of the switching converter,the buck converter running in discontinuous conduction mode ( DCM ) is studied. By modeling and simulation based on MATLAB,the effects on the circuit status are investigated for three circuit parameters:input voltage Vi,capacitance C and inductance L.Under the selected conditions,the transformation of converter from steady-state to bifurcate to chaotic is observed by changing three circuit parameters.The simulation results show that three circuit parameters affect the system in different ways.Compared to continuous conduction mode,the discontinuous conduction mode shows more complicated change rules.Based on the model,a chaos control strategy is used to suppress chaotic motions in the voltage control buck converter running in discontinuous conduction mode.The chaos control strategy is fast and effective.It only takes 0.6 μs to control the system from chaos to stability.Besides,the chaos control strategy doesn't need to set a predetermined trajectory.It just needs to adjust one external parameter,and it is independent of internal circuit parameters.Thus,the correctness of the model is verified and an effective chaos control method is provided. Key words:buck converter;discontinuous conduction mode ( DCM );chaos control
引言
随着电力电子技术的发展,DC-DC 开关变换器被广泛应用于工业和生活的各个领域。作为能源变换的核心部分,DC-DC 开关变换器的性能直接决定了整个负载系 统的工作状态,因此对DC-DC 开关变换器的研究一直是电力电子技术研究中的重点。
DC-DC 开关变换器是一种典型的非线性时变系统和 分段光滑系统,其内部开关器件高频切换导致的非线性 行为极大地增加了系统的复杂性[1-3] 。当电路参数变化 时,开关变换器会出现倍周期分岔、边界碰撞分岔、 Hopf 分岔和混沌等非线性现象[4-9],表现在外部形式即为开关变换器发出较大噪声、输出功率产生波动或者间歇振荡,严重时甚至导致系统运行崩溃[10-11],因此控制 开关变换器工作于稳定的周期状态具有重要意义[12] 。
目前,对DC-DC 开关变换器的非线性现象的研究 并不少,但大部分研究都集中在电感电流连续导通模式 ( CCM ) 的电路[13-16 ],而对电感电流断续导通模式 ( DCM) 电路的研究较少。DCM 模式电路在中低功率范 围的场合应用较广,在该场景下相比CCM 模式具有高的 转换效率和更快的响应速度[17-18],因此对DCM 模式变换器的研究是十分有必要的。本文以工作于DCM 模式的电压控制BUCK 变换器为例,通过MATLAB 建模仿真,研究了不同参数对DCM 模式BUCK 变换器工作状态的影响。在此基础上采用一种混沌控制策略,实现了DCM 模式BUCK 变换 器的混沌控制。仿真结果表明该控制策略快速有效,在验证仿真模型正确的同时也提供了一种有效的混沌 控制方法。
1 DCM 模式BUCK 变换器的建模
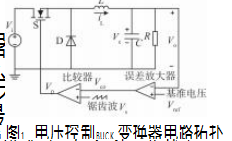
图1为电压控制BUCK 变换器的电路拓扑,其中误差放大器与比较器组成了反馈回路,用以控制开关管导通或者关断,最终实现稳压输出。当BUCK 变换器工作于DCM 模式时,包含3种工作状态:开关管导通、开关管关断(电感电流iL 不为0) 、开关管关断(电感电流iL 为0) 。
假设电路中所有元器件均为理想器件,将输出电容 电压VC 和电感电流iL 作为状态变量,当开关管处于导 通状态时,可列出式(1 ) [ 19-20] 。
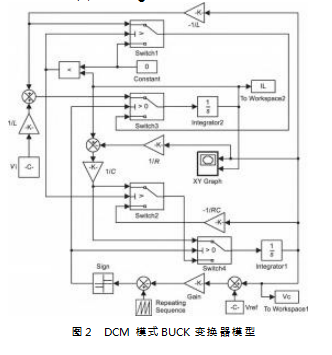
在用MATLAB 进行建模时,需要对3种工作模式进 行选择。具体思路是:首先判断电感电流iL 是否为0. 若iL=0.则电路适用式(3 );若iL ≠0.则继续判断开 关管处于导通还是关断状态,若为导通状态,电路适用 式(1 ),否则电路适用式(2 )。据此在MATLAB 中搭建的仿真模型如图2所示。
该模型中含有4 个Switch 模块,其中Switch1 和 Switch2 为第一级比较,其控制端的信号为比较器的输 出,作用是在比较器判断电感电流是否为0后,选通不 同的状态模式。若比较器输出为0.即电感电流为0.此 时,Switch1 和Switch2 分别将各自输入端口3 ( 下端) 的输入进行输出,此时仿真模型与状态方程式(3 ) 一 致。Switch3 和Switch4 为第二级比较,其控制端的信号由误差放大的反馈信号与锯齿波发生器的输出经过相减后取符号得到,作用是根据计算结果选择模型处于开关管导通状态还是关断状态。
2 电路参数影响的仿真分析
DCM 模式电压控制BUCK 变换器的仿真参数选取如下,参考电压Vref =5 V,开关周期T=200 μs,斜坡电压 的最小值VL =4.81 V,斜坡电压的最大值VH =9.82 V, 负载电阻R=50 Ω,误差放大系数GGain =9.97.将输入电压Vi、电容C和电感L 作为研究的变量。由于BUCK
变换器工作于DCM 模式需要满足公式RT ( 1 -D )>2L[21 ], 其中D 为变换器的占空比,因此在研究DCM 模式下电路 参数对工作状态的影响时,各参数之间存在一定的制约 关系,需要合理选取参数的变化范围以确保电路一直工作于DCM 模式。
2.1 输入电压Vi
研究输入电压Vi 对系统的影响时,令电容C=200 μF, 电感L=2.5 mH,Vi 的变化范围为20 ~40 V,此时电路始终工作于DCM 模式。
在利用上述搭建的仿真模型研究Vi 对系统状态影响时,需要不断改变Vi 重复进行仿真,然后在每一个周期的开始阶段对电容电压VC 进行离散采样。为了保证采样数据的准确,需要确保采样时系统已完成导通时的暂态过程,因此单次仿真时间不能过短,且暂态过程的数据需要舍弃,只保留稳定后的数据。此处将单次仿真时间设定为0.05 s,且只选取最后50 个数据值。
由于仿真中需要不断改变Vi,可在MATLAB 中利用脉冲发生器和计数器模块搭建模型来实现Vi 的自动修改,具体方法为:Vi 的初始值为20 V,每隔0.05 s 脉冲 发生器产生1个脉冲信号,计数器接收到信号后将Vi 的 值增加0.1 V,总仿真时间设为10 s,输入电压Vi 从20 V阶梯上升到40 V。在研究电容C 和电感L对系统状态影响时可采用相同思路进行。
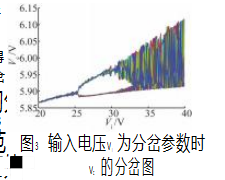
通过仿真模型最终得到以输入电压Vi 作为分岔参数时,电容电压VC 的分岔图如图3所示。从图3可知,当Vi 在20 ~ 25 V 范 围内变化时,系统始终处于单周期稳定态。当Vi 范围为26~30 V 时,系统处于2周 期态,此时电容电压VC 稳定于两个值。随着Vi 继续增 加,系统快速经过倍周期态,进入混沌状态。对比参考 文献[15 ] 可发现,在选定的参数条件下,DCM 模式BUCK 变换器系统状态受输入电压Vi 影响的变化趋势与CCM 模式相同,均是随着输入电压Vi 的增加,系统逐渐从稳定态转变至倍周期态,最终到达混沌态。
2.2 电容C
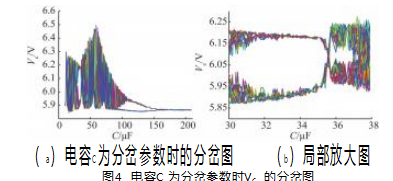
研究电容C 对系统的影响时,令Vi =20 V,电感L =2.5 mH,电容C的变化范围为10 ~ 210 μF,此时电路始终工作于DCM 模式。利用搭建的仿真模型得到以电容C 作为分岔参数时,电容电压VC 的分岔图如图4 ( a ) 所示。由图4 ( a ) 可知,当电容C 从210 μF 逐渐减小 的过程中,系统经历了从单周期稳定态到2周期态,再 到4周期态,最后进入混沌态。然而当电容C 继续减小 到36 μF 左右时,系统又重新进入了单周期稳定态,如 图4 ( b ) 所示。在10 ~ 36 μF 区间范围内,系统又重复 之前的变化规律。相比较CCM 模式,DCM 模式BUCK 变换器展示了更为复杂的变化规律。仿真中出现的稳定- 混沌-稳定-混沌的变化过程,也说明混沌现象只发生在 某一界定的参数范围内,据此需要对参数进行合理选取,以保证系统始终处于稳定的单周期态。
2.3 电感L
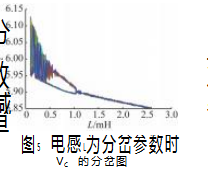
研究电感L对系统的影响时,令输入电压Vi =20 V, 电容C=200 μF。为保证电路工作于DCM 模式,电感L 取值不能过大,选取电感L 的变化范围为0.1 ~ 3 mH,此时电路始终工作于DCM 模式。利用搭建的仿真模型得到以电感L作为分岔参数时,电容电压VC 的分岔图如图5所示。从图可知,在选取的电路参数范围内,随着电感L的减小,系统也经历了从单周期稳定态到混沌的过程。上述仿真结果说明,当BUCK 变换器工作于DCM 模式时,系统的工作状态同时受多个电路参数共同影响。 尽管各个电路参数对系统状态的影响方式互不相同,但产生的机理是一致的。混沌吸引子突变引起了“内危机”,吸引子的尺寸增大,变换器开关由固定的“导通- 关断-导通-关断”状态转向不规则的“导通-关断-关断” 状态,导致周期跳跃和边界碰撞,最终一系列的碰撞分岔使得系统进入混沌状态。在设计时,可以基于该仿真模型预先对系统的运行 状态进行模拟仿真,实现电路参数的合理选取,避免系统进入混沌状态。
3 DCM 模式的混沌控制
3.1 混沌控制策略
分析式(6 ) 可知,γ 作为外部可调参数,当其取值 为0时,式(6 ) 退化为式(4 ),此时式(6 ) 不受控,其系统状态中包含多个不稳定的周期轨道。当0<γ < 1时,式(6 ) 处于受控状态,此时原系统中不稳定周期轨道将被引导到稳定的周期轨道。
3.2 DCM 混沌控制仿真
对于DCM 模式电压控制BUCK 变换器,VC 和iL 是 状态变量,因此式(1 ) 可改写为:
为确保BUCK 变换器受控后仍工作于DCM 模式,需 要在开关管关断时不施加控制,因此式(2 ) 与式(3 ) 不变。根据式(7 ) 得到受控后的DCM 模式BUCK 变换 器(开关管导通)数学模型为:
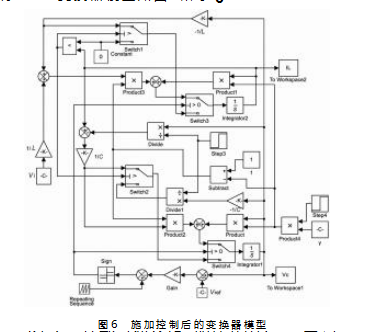
根据式(8 ) 搭建出施加控制后的DCM 模式电压控制BUCK 变换器模型如图6所示。图6中,外部可调参数γ 取值范围在0~ 1 之间,γ 取值越大,意味着控制程度越深。此处选取电路参数为 Vi =40 V,C=200 μF,L=2.5 mH,其余参数保持不变。 根据第2节仿真结果可知,在该电路参数条件下,若不 施加控制,系统将处于混沌状态,而在施加控制后,通 过仿真结果可知,随着γ 值变大,系统逐渐从混沌状态 过渡到8周期态,再到4周期态、2 周期态( 图7),最 后到达单周期稳定态,且控制后的系统均处于DCM 模 式,验证了控制策略的有效性。
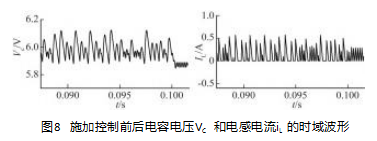
将仿真时间设置为0.2 s,在t=0.1 s 时加入控制 ( γ=0.6 ),得到施加控制前后电容电压VC 和电感电流iL 的时域波形如图8所示。从图中可以看出,系统在0.1 s 之前处于未受控状态,此时电容电压VC 和电感电流iL 的时域波形杂乱无章,在0.1 s 后仅经过0.6 μs,两者的 时域波形就变为稳定的单周期波形,这说明施加控制后的系统快速的完成了混沌抑制现象。该控制策略简单有效,只需要对外部可调参数γ 进行设定,而不依 赖电路自身参数,同时也不需要设定预期的目标轨道, 因此具有广泛的适用性,为混沌控制的研究提供了一种有效的方法。
4 结束语
本文以工作于DCM 模式的电压控制BUCK 变换器作为研究对象,通过MATLAB 建模仿真,分析在DCM 模式下,系统以输入电压Vi 、电容C 和电感L 作为分 岔参数的混沌演化过程,仿真结果表明DCM 模式BUCK 变换器相比CCM 模式具有更为复杂的变化规律。
在设计时,基于该仿真模型预先对系统的运行状态进 行模拟仿真,可以实现电路参数的合理选取,避免系 统进入混沌状态。在此基础上,采用一种混沌控制策 略,实现了将DCM 模式BUCK 变换器的混沌状态控制 到各种倍周期态或稳定态。该控制策略快速有效,不 依赖变换器自身电路参数,且不需要设定预期的目标 轨道,具有广泛的适用性。
参考文献:
[ 1 ] ERICKSON R W,MAKSIMOVIC D. Fundamentals of power electronics [ M ].Springer Science & Business Media,2007: 187-264.
[2 ] JAKOBSEN B K,MILLER E R,LMAN A P,et al.The U.S. merchant marine academy liquid cargo handling simulator [ J ]. Marine Technology,1990.27 (4 ):257-264.
[3]杨旭,裴云庆,王兆安.开关电源技术[M].北京:机械工业出 版社,2004:206-213.
[4 ] MAITY S,TRIPATHY D,BHATTACHARYA T K,et al . Bifurcation analysis of PWM-1 voltage mode controlled Buck converter using the exact discrete model [ J ]. IEEE Transactions on Circuits and Systems-I:Regular Papers,2007. 54 (5 ):1120-1130.
[5 ] ZHUSUBALIYEV Z T,MOSEKILDE E,MAITY S,et al.Border collision route to quasi-periodicity:numerical investigation and experimental confirmation [ J ]. Chaos,2006.16:02312211 -0231221.
[ 6 ] MIRANDA M,ALVAREZ J.Bifurcations and chaos produced by the modulation signal in a PWM buck converter [ J ]. Chaos Solitons and Fractals,2009.42:2260-2271.
[7 ] ZHU B M,FAN Q H,LI G Q,et al.Chaos suppression for a buck converter with the memristive load [ J ]. Analog Integrated Circuits and Signal Processing,2021.107 (2 ):309-318.
[ 8 ] YANG Y,LI D,WANG D.Dynamic analysis of the switched- inductor buck-boost converter based on the memristor [ J ]. Electronics,2021.10 (4 ):452.
[ 9 ] 李荣,罗晓曙:.DC-DC buck 变换器的混沌控制[J].广西物理,2005(3)
[ 10 ] DEANE J H B,HAMILL D C.Instability,subharmonics,and chaos in power electronic systems [ J ].IEEE Transactions on Power Electronics,1990.5 (3 ):260-268.
[ 11 ] WOOD J R. Chaos:a real phenomenon in power electronics [ C ]//Applied Power Electronics Conference and Exposition, Baltimore,MD,USA.New York:IEEE,1989:115-124.
[ 12 ] GAO P,MIN F,LI C,et al.Dynamical analysis of boundary behaviors of current-controlled DC-DC Buck converter [ J ]. Nonlinear Dynamics,2021.106 (3 ):2203-2228.
[ 13 ] 高金峰.非线性电路与混沌[M]. 北京:北京科学出版社, 2005:203-217.
[ 14 ] 张波,曲颖.BUCK DC/DC 变换器分岔和混沌的精确离散 模型及实验研究[J]. 中国电机工程学报,2003.23 ( 12 ):99-103.
[15]张同国,高文进,张冀等.基于PI 控制的DC/DC 变换器峰值 电流控制策略[J].机电工程技术,2022.51(05):98-101.
[ 16 ] 王春芳,王开艳,李强.Buck 变换器仿真模型及分岔与混沌 研究[J ]. 系统仿真学报,2007.19 (24):5824-5826.
[ 17 ] 周旭峰.高功率因数DCM Buck PFC 变换器的研究[D ].南 京:南京理工大学,2017.
[18]魏星,黄洪全,汤云骏等.用于燃料电池汽车的双向DC-DC 变换器[J].装备制造技术,2016(7):155-159.
[19]张卫平.开关变换器的建模与控制[M].北京:中国电力出 版社,2005.
[20 ] 王燕,李洁.DC/DC BUCK 变换器的混沌现象分析及其控制 [ J ].电子科技,2014.27 (9 ):143-147.
[21 ] 任海鹏,刘丁.Boost 变换器中混沌现象及其控制的仿真研 究[J ]. 系统仿真学报,2004.16( 11 ):2529-2532.
[22 ] LUO X S,Chen G R,Wang B H,et al. Hybrid control of period-doubling bifurcation and chaos in discrete nonlinear dynamical systems [ J ].Chaos,Solitons and Fractals,2003.18: 775-783.
[23 ] 贾美,张国山.电压控制型BUCK 变换器的混沌控制 [ J ].电子科技大学报,2016.45(2):208-214.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/64839.html