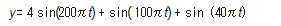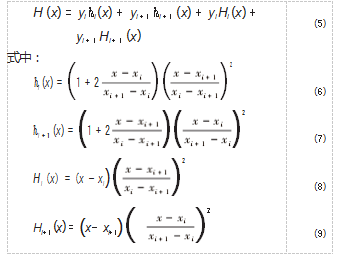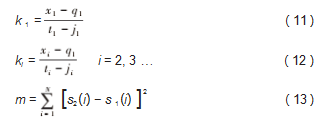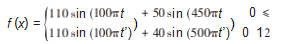SCI论文(www.lunwensci.com)
摘要:为了改善经验模态分解 ( EMD ) 在谐波检测时产生的端点效应, 提出了波形自适应延拓的改进型 EMD 算法 。以信号端点附 近波形的极大值和极小值斜率为基准, 寻找信号内具有相同斜率的一组极大值和极小值, 为了使寻找到的目标波形与端点处的波 形更加相似, 引入波形匹配度函数, 用其数值大小判断两个波形相似程度 。根据端点位置不同, 把寻找到的目标波形前一个或后 一个波形的极大值和极小值向端点处延拓 。在 EMD 分解过程里用分段三次 Hermite 插值函数替代三次样条插值函数, 消除了包络 线过冲和欠冲问题 。通过测量稳态谐波与暂态谐波的实验, 验证了此算法能高效遏制 EMD 端点效应, 显著提升了分解精度 。且测 出的谐波幅值和频率与快速傅里叶 ( FFT ) 相比更精确, 符合电力系统谐波分析要求。
关键词 :希尔伯特-黄变换,经验模态分解,Hermite 插值函数,谐波
Harmonic Detection Method of Coal Mine Power Supply System to Improve EMD End Effect
Ru Ruipeng1. Cao Yudong2. Guo Zhiqiang1. Li Yanjie1. Qi Yi1
( 1. Licun Coal Mine of Cilinshan Coal Industry Co., Ltd. of Shanxi Lu’an Environmental Energy, Changzhi, Shanxi 046200. China;
2. Liaoning Technical University, Fuxin, Liaoning 125105. China)
Abstract: In order to improve the endpoint effect of empirical mode decomposition (EMD) in harmonic detection, an improved EMD algorithm
based on waveform adaptive continuation is proposed. The method takes the maximum and minimum slopes of the waveform near the signal
endpoint as the benchmark, and finds a group of maximum and minimum values with the same slope in the signal . In order to find the target
waveform more similar to the waveform at the endpoint, the waveform matching degree function is introduced, and its numerical value is used to
judge the similarity degree of two waveforms. Depending on the position of the end point, the maximum value and the minimum value of the
waveform before or after the target waveform found are extended to the end point . In the EMD decomposition process, the cubic spline
interpolation function is replaced by the piecewise cubic Hermite interpolation function , which eliminates the overshoot and undershoot of the
envelope. Through the experiments of measuring steady-state harmonics and transient harmonics, it is verified that the algorithm can
effectively suppress the EMD end effect and significantly improve the decomposition accuracy . And the measured harmonic amplitude and frequency are more accurate compared to Fast Fourier Transform (FFT) and meets the requirements of power system harmonic analysis.
Key words: Hilbert-Huang transformation; empirical mode decomposition; Hermite interpolation function; harmonic
引言:小波变换[ 1] 是电网检测谐波的重要方法, 遇到非稳 态信号以及存在间谐波信号时, 小波基的选取严重影响 分解结果, 并且在信号分析过程无法更换小波基, 该小 波基在整体上表现良好, 但在局部可能不佳 。故小波变 换对信号局部变化没有自适应性 。提出利用经验模态分 解 (Empirical Mode Decomposition, EMD ) [2] 方法对谐波 进行分解, 分解后能够有效测量非平稳谐波和观察信号 局部特性, 然而在 EMD 分解过程中, 处理包络线时在信 号两端处会出现严重的发散现象, 伴随着 EMD 的分解影 响逐步增加, 使得在处理信号时得到的结果出现较大偏 差, 得到的谐波频率和幅值出现较大误差。
为了高效处理和解决端点效应, Huang N E 等提出了 信号两侧添加特征波的数学模型, 但不同数据所需的特征 波不同, 在实际应用不可靠; Grilling 提出了镜像延拓法, 但信号端点处多数情况是非极值点, 需要截去端点处一段 信号将镜面放在极值点处, 在处理短信号时效果不佳[3]; Hamza[4]提出了时间序列预测模型, 但仅适应于平稳简单 的谐波信号。当前人们提出的一些高效处理端点效应的方 法中, 还包括特征波法[5] 、 自回归算法[6] 、极值延拓法[7]、 奇偶延拓法[8] 、斜率法[9]等, 但都存在检测信号时抑制端 点效应能力不足的问题 。为此, 提出斜率与波形匹配度 相结合的方法进行自适应延拓, 使得检测的谐波信号更 接近真实值, 能够精确分离谐波信号, 提高检测精确度。
1 EMD端点效应
EMD方法从公布到现在在非线性领域得到广泛的应用, 但在 EMD方法中进行包络线处理时会出现端点效应 问题影响分解结果 。因为所检测的信号端点处多数情况 是非极值点, 所以把极值点当做插值点的三次样条[10]方 式拟合的包络线在端点处经常会出现发散现象, 这种现 象会随着 EMD 的分解不断加重, 影响数据的准确性 。端 点效应问题严重影响了 EMD 的分解结果, 在处理较长的 信号数据时, 可以依据信号两端的极值点分布情况来选 择截去一部分数据长度确保形成的包络线在端点处失真 最小, 但在处理短信号时, 这种方法会导致原本的数据 变得更少, 影响分解的精确性, 但是在信号两端分别延 拓一对极值点, 把延拓的极值点当做端点处所需的插值 点进行拟合包络线, 上述问题得以解决 。如果构造出的 极值点能够有效模仿信号两端的趋势走向, 那么这种延 拓能够有效抑制端点效应 。端点处进行数据延伸是处理 和解决 EMD端点效应问题的高效方式, 如镜像处理方 法 、根据神经分布网络延拓模式 、根据多项式拟合的延 伸方法等, 这些方法的本质都是通过在信号两端构造一 对极值点并且能够有效仿造信号在两端的趋势, 进而有 效改善拟合包络线产生的端点效应 。信号两端延拓的质 量直接影响端点效应的抑制效果。
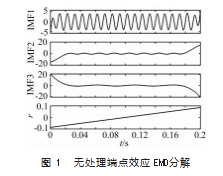
以上分析可知 EMD在分解谐波信号时会出现端点效 应现象, 使得 EMD 分解得到 IMFs 出现结果偏差, 严重影响实验结果 。采用仿真信号一进行验证:
2 改进的 EMD算法
2.1 Hermite插值法拟合包络线
Hermite插值法[11]构造的三次插值函数, 将信号的极 值点看做是插值点, 所有极值点所在的区间插值函数连续而且极值点处插值函数极度平滑, 将三次样条插值代 替为三次 Hermite插值, 从而解决了包络线在端点处产生 欠冲与过冲的严重问题, 具体算法如下。
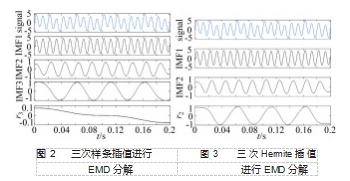
由式 ( 5) 和式 ( 10) 可构造信号的上下包络线 。依 旧采用仿真信号一进行分解, 采样频率为 1 000 Hz, 采 用镜像法消除端点效应, 图 2所示为用三次样条插值进行 EMD分解, 图 3所示为三次 Hermite插值进行 EMD分解。 对比图 2、图 3 可以看出, Hermite插值的方法可以准确 分解出信号的 3个谐波分量, 且没有多余的余项, 证明 了 Hermite插值可以有效抑制端点处包络线过冲与欠冲现 象, 使得 EMD可以准确分解出信号的谐波分量。
2.2 信号的端点延拓
由于信号两端进行的延拓必须表现出原来信号的趋 势走向, 确保延拓的极值点具有实际意义 。对于谐波来 说, 信号规律性强, 本文提出了斜率与波形匹配度相结 合的方法可以确保延拓波形可以表现出信号的趋势走向。
设 ki 为不同组极值点的斜率, 匹配度 m 有:
当 k 1=ki, 且 m 小于一定的数值 (本文给定的数值为 4 ) 时, 将目标波形根据不同端点将前一个或者后一个波 形的极大值和极小值向两端点处延拓; 如果找不到符合 条件的波形, 左端点为例, 将信号左端相临近的两个极 极值点对应的y 轴均值和x 轴均值向左延拓, 右端点同理。
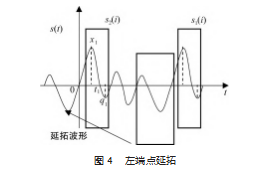
图 4所示为左端点延拓示范。
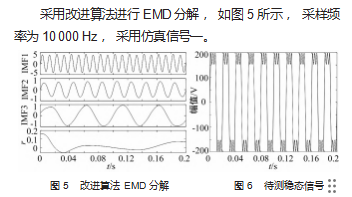
由图 1 和图 5 进行比较可以看出, 改进的 EMD 算法 能够有效改善端点效应问题, 使测得的各个谐波的频率 和幅值更加精确。
3 仿真实验
3.1 稳态谐波检测
在稳定的状态下, 实际中常见的信号一般包括 3 次 谐波和 5 次谐波[ 12- 14], 因此采用仿真信号二:
f(t) =220sin( 100πt)+66sin( 300πt)+44sin( 500πt)
f(t)的波形如图 6 所示 。用 EMD 进行分解, 采样频 率和采样点数分别为 10 kHz 和 2 000.
EMD 分解结果如图 7 所示 。 由图可知 EMD 分解最终 结果可以直观地观察信号随时间改变的实际状况 。在图 中, 实线是 EMD 分解获取的信号变化波形, 虚线反映信 号真实的变化波形 。可以看出, IMF1 和 IMF2在端点处 产生发散问题, 但总体与实际信号基本一致 。IMF2 在幅 值方面存在误差, 端点处误差较大, 但整体频率拟合基 本一致, 误差在可控范围内 。 由此可见, 改进后的 EMD 可以有效地将信号中常见的谐波分量分解出来, 幅值和 频率的数值都在允许误差范围内变化。
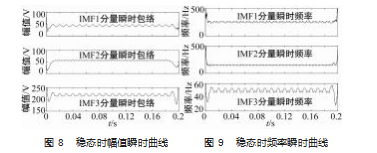
图 8 和图 9 分别表示的是 EMD 分解得到的各个谐波 分量的幅值和频率随时间变化曲线, 是每个 IMFs 分量对 应的瞬时包络 。 由图可以看出, 幅值和频率在端点处存 在误差, IMF1 和 IMF3 幅值在允许误差内有些许波动, IMF2 幅值相对平稳 。IMF1 和 IMF2 频率变化稳定, IMF3 存在些许波动 。但是分解的 IMFs 的幅值和频率与实际信 号基本保持一致。
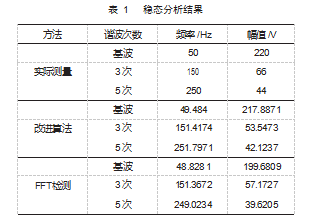
表 1 详细列举出了仿真信号二的实际幅值和频率的 数值, 以及根据改进算法和快速傅里叶 ( Fast Fourier Transform, FFT ) [ 15] 算法检测出的幅值和频率的数值 。FFT 传统算法和改进算法所得基波分量的频率与真实值 对比得到的相对误差依次为 2.34% 和 1.03%, 幅值的相 对误差依次为 9.23% 和 0.96%; FFT 传统算法和改进算法 所得 3 次谐波分量的频率与真实值对比得到的相对误差 依次为 0.91% 和 0.93%, 幅值的相对误差依次为 13.63% 和 18.86%; FFT 传统算法和改进算法所得 5 次谐波分量 的频率与真实值对比得到的相对误差依次为 0.04% 和 0.71%, 幅值的相对误差依次为 9.96% 和 4.26% 。以上数 据进行对比分析得出, FFT 在检测给定信号的幅值时存 在较大误差, 这与 FFT 的频谱泄漏有关, 虽然改进的算 法在谐波的频率计算上与 FFT 检测差距不大, 但测量谐 波的幅值整体上优于 FFT 算法。
3.2 暂态谐波
在电力系统出现故障问题以及处理的过程中, 电力系统会出现间谐波[ 16] 。采用的暂态仿真信号三:
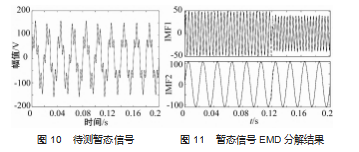
该波形图像如图 10 所示 。对其进行 EMD 分解从而 得到 IMFs 。设采样频率为 10 000 Hz, 采样点为 2 000.
暂态仿真信号 EMD 分解结果如图 11 所示, IMF1 包 含 2 个谐波分量, IMF2 是基波分量 。实线是 EMD 分解获 取的信号变化波形, 虚线反映信号真实的变化波形 。 由 图 11 可以看出, IMF1在端点处和 0. 12 s 处与实际波形相 比存在较大误差, 其他则基本拟合一致, IMF2 整体拟合 效果良好, 则改进算法适合非稳态条件下含有谐波甚至 间谐波的检测。
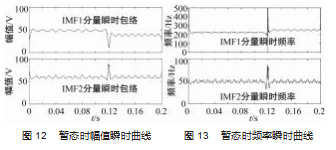
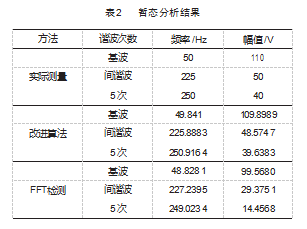
图 12 和图 13 是各个 IMFs 分量对应的瞬时包络 。可 以看出, 两者在 0. 12 s 附近都存在较大的波动, 对应了 给定信号在 0. 12 s 的变化, 可以看出 EMD 分解后可以有 效辨别信号变化时刻 。其他时间点的幅值和频率都在误 差允许区间内波动, 与实际的频率和幅值变化趋势整体 上保持协调一致。表 2 详细列举出了仿真信号三的幅值和频率的数值, 以及根据改进后的算法和 FFT 算法检测出的数值 。FFT 传统算法和改进算法所得基波分量的频率与真实值对比 的得到相对误差依次是 2.34% 和 0.31%, 幅值的相对误 差依次是 9.48% 和 0.09%; FFT 传统算法和改进算法所得 间谐波分量的频率与真实值相比得到的相对误差依次为 0.20% 和 0.39%, 幅 值 的 相 对 误 差 依 次 为 41.24% 和 2.85%; FFT 传统算法和改进算法所得 5 次谐波分量的频 率与真实值对比得到的相对误差依次是 0.39% 和 0.36%, 幅值的相对误差依次是 63.86% 和 0.90% 。从误差分析数 据上看, FFT 在面对含有间谐波的信号时表现不佳 。 FFT 检测间谐波与 5 次谐波的幅值检测误差在 50% 左右, 而改进的算法检测结果误差全部维持在 1% 以下, 因此, 在非稳态条件下, 改进的算法能够有效检测出谐波分量 甚至间谐波并且直观地观察出谐波分量的变化时刻。
3.3 算例仿真比较
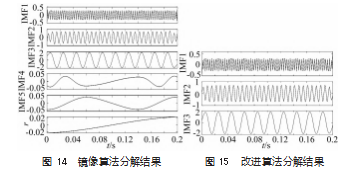
为了验证改进算法比传统算法更加优越, 将该算法 与文献[ 17]所提的镜像算法进行比较, 采样频率与仿真信 号与该文献一致, 两种算法各自的仿真结果分别如图 14 和图 15 所示。
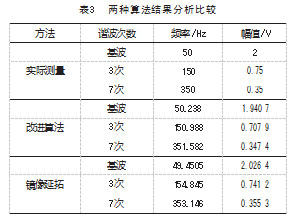
改进算法的检测结果与镜像延拓法算法检测结果如 表 3所示 。 由表可知, 镜像算法和改进算法所得基波分 量的频率与真实值相比得到的相对误差依次为 1.09% 和 0.47%, 幅值的相对误差依次为 1.34% 和 2.96%; 镜像算 法和改进算法所得 3 次谐波分量的频率与真实值相比得 到的相对误差依次为 3.23% 和 0.65%, 幅值的相对误差 依次为 1.17% 和 4.21%; 镜像算法和改进算法所得 7次谐 波 分 量 的 频 率 与 真 实 值 相 比 得 到 的 相 对 误 差 依 次 为 0.89% 和 0.45%, 幅值的相对误差依次为 1.51% 和 0.74%。 由分析数据可以看出, 改进算法在幅值测量方面更加精 确, 在频率方面, 测量的 7 次谐波频率更加精确, 其他 谐波和镜像延拓法相比相差不多 。因此提出的改进算法 整体上优于镜像延拓算法。
4 结束语
( 1) 提出的基于斜率与波形匹配度相结合的算法可 以有效抑制 EMD端点效应现象, 可以将不同次谐波有效 分解出来, 更加直观地观察各次谐波随时间的变化情况, 在间谐波的提取方面也有一定的优势。
( 2) 相比于 FFT 检测谐波, 该算法不仅在谐波检测 的频率和幅值方面更加精确, 而且在检测不同谐波所得 数据的准确性更加稳定, 在检测间谐波和暂态信号方面 更具有优势。
( 3) 该算法能有效对谐波进行分解, 能精确地分离 出不同频率的谐波, 可直观地反映所测信号中谐波含量, 提高了谐波频率与幅值参数的检测精度 。相比于镜像延 拓算法, 该算法有效地抑制了端点效应。
参考文献:
[1] 肖勇,李博,尹家悦,等 .基于小波变换和小波包变换的间谐波 检测[J]. 智慧电力,2022.50(1):101-107.
[2] Zhu Guorong, Peng Sha, LaoYongchang. Short-Term Electricity
Consumption Forecasting Based on the EMD-Fbprophet-LSTM Method[J]. Mathematical Problems in Engineering,2021.
[3] 徐力彬,宋余庆,刘毅 .基于镜像延拓和窗函数的端点效应抑 制方法[J].计算机工程,2015.41(4):112-116.
[4] Hamza Daoudi. Application of ARMA Models in Forecasting Electricity Production With Box-Jenkins Method(Case of Algeria) [J]. International Journal of Statistics & EconomicsTM,2020.21(1).
[5] 魏东栋,汤文成 . 基于序贯相似性检测和自适应滤波的 EMD 端 点 效 应 处 理 方 法 (英 文)[J].Journal of Southeast University (English Edition),2021.37(1):14-21.
[6] Mei Yun, Jiang Haiyang, Lin Ying. Parameter Estimation Algo ⁃ rithm and Application in Industry Design[J]. Journal of Physics: Conference Series,2019.1187(4).
[7] 岳晓峰,邵海贺 .基于相似极值延拓的 EMD 端点效应改进方 法[J].组合机床与自动化加工技术,2015(9):78-80.
[8] Feng Shaowei. Processing method of EMD endpoint effect based on SVRM extension[J]. Vibro Engineering PROCEDIA,2020(35).
[9] 梁黎明,王茂芝,徐文皙,等 . 综合斜率和三次样条的 EMD 端点 效应抑制方法[J].振动与冲击,2022.41(14):70-76.
[10] Liu Zaoling, Wang Menglin, Fan Yong. Bidirectional regulation of BDE-47 on 3T3-L1 cell differentiation based on a restricted cubic spline model[J]. Toxicology and Industrial Health,2022. 38(8).
[11] Pu Yasong, Shi Yaoyao, Lin Xiaojun. Joint Motion Planning of Industrial Robot Based on Modified Cubic Hermite Interpola⁃ tion with Velocity Constraint[J]. Applied Sciences,2021.11(19).
[12] Wu Tiezhou, Wang An, Xu Yawen. A rapid harmonic detection method for grid-connected photovoltaic when three-phase volt⁃ age is unbalanced[J]. International Journal of Low-Carbon Tech ⁃ nologies,2021.16(3).
[13] 万留杰,甄超,邱宗甲,等 .基于 FFT滤波高精度光声二次谐波检 测技术的研究[J].光谱学与光谱分析,2020.40(10):2996-3001.
[14] 孙曙光,田朋,杜太行,等 .基于 apFFT-AMD 的密集频率谐波/ 间谐波检测[J]. 浙江大学学报(工学版),2020.54(1):178-188.
[15] Zhang Shuang, Tian Bei, Liang Jian. Detection of Harmonic Components using the FFT and Instantaneous Reactive Power Theory[J]. Journal of Physics: Conference Series,2022.2242(1).
[16] 李文番,张国钢,钟浩杰,等 .一种高频率分辨率的谐波 、间谐 波分析模型[J]. 电工技术学报,2022.37(13):3372-3379.
[17] 顾小兴,金涛,郭艳威 . 改进 EMD端点效应电力系统 HHT谐 波检测研究[J]. 中国测试,2015.41(3):99-102.
作者简介:
茹瑞鹏 ( 1979-), 男, 山西长治人, 硕士, 高级工程师, 研究 领域为煤矿机电。
曹宇东 ( 1999-), 男, 山西晋中人, 硕士研究生, 研究领域为 谐波检测。
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63995.html