SCI论文(www.lunwensci.com):
摘要 :提出将行波反射法用于断路器分合闸线圈的匝间短路故障定位, 通过有限元仿真计算分合闸线圈的电容 、 电感矩阵, 基于 ATP-EMTP 建立线圈的波阻抗模型 。在绕组首端注入低压方波脉冲信号, 获得发生匝间短路故障时的首端反射波特征曲线 。采用 覆盖法计算了反射波特征曲线的盒维数 、关联维数与信息维数 。结果表明: 随短路位置变化, 特征曲线盒维数未呈现明显的变化 规律, 关联维数与信息维数逐渐降低, 且各层绕组匝间短路之间的关联维数具有良好的区分度 。将短路故障位置划分为 4 段, 以 盒维数 、信息维数与关联维数作为输入参数, 使用 BP 神经网络进行短路故障的定位 。仿真结果表明: 测试集故障定位准确率为 100%, 该方法具有可行性。
关键词 :行波反射法; 分合闸绕组; 波阻抗; 分形维数; BP 神经网络
Research on Fault Location of SF6 Circuit Breaker Opening/Closing Coil Based on Traveling -wave Reflection Method
Abstract: Traveling-wave reflection method is used into locating the inter-turn short circuit fault of the SF6 circuit breaker opening/closing coil, the capacitance and inductance matrix of the opening/closing coil are calculated through finite element simulation , and the wave impedance model of the coil is established based on ATP-EMTP . Low voltage square wave pulse signal is injected into the start end of the winding, and the reflection wave is obtained at the start end. The box dimension, correlation dimension and information dimension of reflection wave characteristic curve are calculated by using covering method . The result shows that with the change of short circuit position, the dimension of the feature curve box does not show obvious change rule, the correlation dimension and information dimension gradually decrease, and the correlation dimension between the interturn short circuit of each layer has good differentiation . The location of short-circuit fault is divided into four sections, with the box dimension, information dimension and correlation dimension as input parameters, and BP neural network was used to locate short-circuit fault combined with fractal dimensions . The simulation results show that the accuracy of fault location in test set was 100%, indicating that the method is feasible.
Key words: traveling-wave reflection method; opening/closing coil; wave impedance; fractal dimension; BP neural network
0 引言
断路器作为电力系统的重要设备之一, 既起着带电 切合正常负荷电流的控制作用, 也起着在规定的时间内 承载 、开断和关合异常电流的保护作用, 对于保证电力 系统的安全可靠运行具有十分重大的意义[ 1-2] 。而分合闸 线圈作为断路器操动机构的重要器件, 很大程度地影响 了断路器动作的可靠性 。对于运行中的断路器, 由于电、 热及环境等多方面因素的影响, 其分合闸线圈的绝缘漆 逐渐老化, 造成绝缘性能下降, 可能导致匝间短路故障 和层间短路故障 。出现轻微短路故障时, 即使断路器仍 能正常动作, 但是线圈的电阻下降会导致工作时通过线 圈的电流增大, 线圈发热严重, 严重时造成线圈烧损,影响断路器的分合闸功能导致拒动, 从而影响电网的稳 定运行[3-7] 。因此, 及时地发现分合闸线圈的绝缘故障从 而采取相应的检修措施, 对于提高断路器可靠性具有十分重大的意义。
工程实际中通过测量分合闸线圈的直流电阻来判断线圈是否存在匝间短路故障[8-9], 这种方法只能粗略地 判断是否存在故障, 不能进一步揭示短路故障的位置等信息。
行波法最早用于输电线路上的故障定位, 由于其可 靠性高和定位准确而得到广泛应用[ 10- 12], 国内外学者开 展了大量针对故障行波信息的研究 。文献[13]将行波法 应用于发电机转子绕组的匝间短路的诊断中, 分析得出特征波形的起始时间和畸变面积可反映故障位置和故障 程度, 且故障信息的获取取决于注入信号的上升沿, 上 升沿越陡峭则诊断精度越高 。文献[14]将行波法应用于 变压器绕组的匝间短路故障定位中, 通过分析行波在变 压器绕组上的传播特点得出短路匝对应的反射波电压幅 值大于无故障时的对应匝反射波, 从而实现了对匝间短 路故障的定位 。 目前还未查到有关小型线圈绝缘故障的 相关研究。
本文将行波反射法引入 SF6 断路器分合闸线圈匝间 短路的故障定位中 。通过有限元软件和 ATP-EMTP 建立 分合闸线圈的波阻抗模型 。在模型首端注入高频低压脉 冲并检测反射波曲线, 通过将短路前后的反射波曲线作 差得到特征曲线 。计算特征曲线的盒维数 、信息维数与 关联维数, 分析不同短路位置下的变化规律, 结合 BP 神 经网络进行分合闸线圈匝间短路故障位置的诊断。
1 行波反射法
1.1 行波理论
当行波沿导线传播,遇到波阻抗发生突变的节点时, 由于在节点前后单位长度导线的电场能和磁场能保持不变, 而单位长度导线的电容和电感都 发生变化, 行波的电压 、电流的幅值都要产生改变, 即 发生行波的折射和反射[ 15] 。反射波与折射波的大小通过 反射系数和折射系数求得 。如图 1 所示, 波阻抗为 Z1 和 波阻抗为 Z2 的线路在点 A 相连, 当电压行波 u1 在传播至 点 A 时, 线路波阻抗由 Z1 突变为 Z2, 发生折射与反射 。 产生的折射波 u12 沿着与行波 u1 相同的方向传播, 其表达 式如式 ( 1 ) 所示; 而反射波 u11 沿着与行波 u1 相反的方 向传播, 其表达式如式 ( 2 ) 所示。
1.2 行波反射法原理
行波反射法基于输电线路故障的单端行波定位法提出, 对故障绕组发出直流低压脉冲信号, 测量脉冲产生 的反射波进行故障的定位识别。
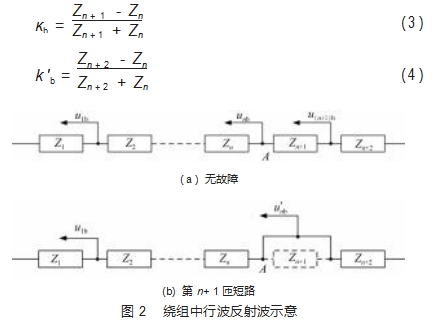
由于分合闸线圈线匝长度远大于邻近线匝之间的距离, 电磁边界在线匝换位处不连续, 相邻线匝换位处波 阻抗产生明显的变化, 因此可将每一匝线圈等效成一段 传输线, 对应一个波阻抗值 。在绕组的一端施加低压脉 冲信号, 由于每一匝线圈等效波阻抗值不同, 脉冲波经 过每一匝线圈时都发生折射与反射, 产生的反射波经过 多次折射回到信号输入端, 如图 2 ( a ) 所示 。而当发生匝间短路故障时, 故障位置点后的波阻抗值改变, 此处 波阻抗突变点的反射系数也随之改变, 产生的反射波幅 值也随之变化, 如图 2 (b) 所示 。当波阻抗 Zn+ 1 被短接 后, 点 A的反射系数由 kb 改变为 k, 此处的反射波 u1n 幅 值也发生变化, 此时在输入端检测反射波, 前 n-1 个反 射波与无故障时相同, 而第 n 个反射波 unb 发生突变 。因 此发生匝间短路故障时, 输入端检测得到的反射波曲线 不同于无故障时的反射波曲线 。将故障前后的反射波曲 线作差即可获得包含短路故障位置信息的特征曲线。
2 模型建立
2.1 分合闸线圈有限元模型
典型分合闸线圈如图 3 所示, 采用连续式缠绕方式, 每层有 175 匝, 共 21 层, 额定电压为 220 V, 导线为直 径 0.25 mm 的铜导体漆包线 。 由于线圈匝数过多, 以线 匝为单位建立有限元模型计算量过大 。 同时考虑到实际 发生绝缘故障时, 通常多匝同时烧熔, 故对其采取简化 等效, 将每层相邻的 25 匝视为一个整体, 每层等效为 7 匝, 每匝彼此独立, 层数为 21 层保持不变。
基于有限元软件建立分合闸线圈的模型并进行其电 感电容参数的计算 。其三维有限元模型如图 4 ( a ) 所 示, 包含铁心 、外壳与绕组 。考虑它具有轴对称特性,将它简化为二维轴对称模型以在保证计算精度的情况下 减小计算量, 如图 4 (b) 所示。
2.2 电感电容矩阵的计算
电容为储能元件, 先计算导体储存的电场能量, 再 通过电场能量计算导体的电容, 通过静电场模块计算电 容矩阵 。每次将某一线圈设为端子, 施加单位电压, 计 算电场能量, 进而计算相应的电容参数[ 16], 其计算公式如式 ( 3 ) ~ ( 4 ) 所示。
式中: Cii 为导体的自电容即对地电容; Cij 为导体 i 和导 体j 之间的互电容; Vi 、Vj 分别为导体 i、j 的电势; We 为 整个系统的能量。
通过磁场模块计算电感矩阵, 其计算公式如式 ( 5 )~ ( 6 ) 所示。
式中: Lii 为导体的自电感; Lij 为导体 i 和导体j 之间的 互感; Ii 、Ij 分别为通过导体的电流; Wm 为整个导体的 能量。
2.3 波阻抗模型
基于 ATP-EMTP 建立分合闸线圈等效波阻抗电路模型, 每层 7 匝等效为 7 个波阻抗, 共 21 层, 每一层的第 一匝与上一层最后一匝相连, 共 147 个波阻抗, 如图 5 所示 。前期仿真发现, 由于线匝长度较短, 对输入波形的 频率要求很高, 最终选择在首段施加幅值 10 V, 上升、 下降沿均为 0.05 μs, 脉宽 0. 15 μs 的方波脉冲信号, 如图 6 所示。
3 反射波特征曲线分析
3.1 反射波曲线
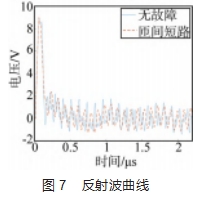
设置匝间短路故障, 在输入端测得其反射波曲线与 无故障时的反射波曲线, 如图 7 所示 。可见, 不存在匝 间短路故障时, 首端能够检测到一系列的反射波, 这是 由于每一匝线圈的电容与电感参数不同, 波阻抗不同, 因此注入的电压脉冲在经过每个波阻抗时均发生折 、反 射, 从而形成一系列的反射波回到首端 。第 1 个反射波 的幅值最大, 为 9.02 V, 第 2 个反射波幅值略微降低, 随后经过多次折反射后, 反射波的幅值迅速衰减至 2.5 V 以下 。存在匝间短路故障时, 第 1 个反射波与无故障时 幅值相差较小, 随后反射波幅值同样迅速衰减, 各反射 波的幅值和达到首端的时间与无故障时有一定差别, 反 射波曲线整体变化趋势与无故障时相似。
为更好地挖掘反射波曲线中蕴含的故障信息, 将存 在匝间短路故障的反射波曲线与无故障时的曲线作差获 得特征曲线 。第 1 层第 1 、2 、3 匝短路故障的特征曲线如 图 8 所示, 其波形呈现出高度非线性 、不平稳的特点, 幅值随时间未呈现出明显的变化趋势 。特征曲线随短路 位置的变化也未呈现出时间或幅值上的变化规律。
第 1~4 层第 1 匝短路时的特征曲线如图 9 所示 。第 1 层特征曲线幅值显著大于第 2 、3 、4 层, 最大达到 3.8 V 。第 2 、3 层的特征曲线的幅值相近, 最大达到 0.5 V 左 右 。第 4 层的特征曲线幅值最大仅达到 0.2 V 。波形随短 路位置的变化较为复杂 。第 1 层故障特征曲线呈现为多 簇形状不规律, 幅值相差不大的反射波 。第 2 层故障特 征曲线幅值随着时间增加逐渐增大, 且曲线整体存在一 个低频的分量 。第 3 层故障特征曲线表现为几个低频分 量的叠加, 在曲线的后半部分逐渐出现幅值较小的高频分量 。第 4 层故障特征曲线逐渐呈现出按正弦规律变化 的趋势, 但曲线上表现为毛刺的高频分量幅值逐渐增大。
可见, 不同短路位置的特征曲线未显示出清晰的变 化规律 。这是由于当存在匝间短路故障时, 该点折射系 数与反射系数发生变化, 产生不同于无故障时的反射波 与折射波, 反射波与折射波在传播过程中同样产生无数 次的折反射 。 同时每一匝的波阻抗不同, 不同短路位置 对折反射系数的影响也不同, 产生的反射波与折射波传 播到首端的路径也不同 。因此, 不同位置波阻抗短路对 波形造成的影响十分复杂, 难以直接描述。
3.2 广义分形维数
分形的本意为不规则的 、分数的 、支离破碎的物体, 可以理解为局部和整体在某个方面具有相似性[ 17] 。分形 维数是分形理论中一个十分重要的概念, 它可以量化研 究对象的无序性与复杂程度, 从而有效地刻画复杂非线 性非平稳系统的行为特征[ 18] 。分形维数以数值的形式刻画出研究对象不规则性的变化, 从而反映出系统的运行 状况, 具有简单直观的特点, 在基于振动信号的设备异 常状态的判断 、设备故障的识别分类和设备故障的早期 预测等领域得到了广泛的应用[ 19]。
由图 8~9 可见, 分合闸线圈的反射波特征曲线具有 非线性非平稳的特点, 在几何上存在一定的自相似特性, 同时随着短路位置的变化, 反射波特征曲线的不规则性 也发生明显变化 。因此, 将广义分形维数引入分合闸线 圈匝间短路故障的定位研究中。
采用覆盖法计算广义分形维数, 使用 N 个尺度为 l的 超立方体覆盖研究对象, 设点落入第 i 个盒子的概率为 Pi ( l), 给定 q 值, 计算获得信息熵:
改变尺度 l 的大小, 经计算获得对应的 Kq ( l) 值, 作 出 lg l - Kq ( l) 曲线图, 在标度律存在范围内斜率的绝对 值就是给定参数 q 的 Dq 值。
给定不同的 q 值即可得到不同标度指数子集的广 义 分 形 维 数 。 当 q=0 时, 广 义 分 形 维 数 即 为 盒 维 数; 当 q=1 时, 为信息维数, 信息维数能够更好地反映系 统的动力行为; 当 q=2 时, 为关联维数, 体现点集中 各点之间的关联性强弱, 通过各点之间的距离接近程 度来进行描述 。
实际计算过程中一般使用频率近似计算概率:
式中: di 为落入第 i 个超立方体的点数;

为落入所有盒子的点数。
计算分合闸绕组不同位置匝间短路反射波特征曲线 的盒维数 、信息维数与关联维数, 绕组前 4 层共 28 匝反 射波特征曲线的盒维数 、信息维数与关联维数随短路位 置变化的曲线如图 10 所示。
可见, 盒维数分布在[0.93, 0.98] 内, 变化范围较小, 且随着短路位置靠近绕组末端, 未呈现明显的变化 规律 。盒维数为反映对象的几何测度, 随着短路位置的 变化, 特征曲线的盒维数接近于 1, 其几何测度仅有小 范围的变化。
信息维数随短路位置变化总体呈现逐渐下降的趋势。 对于发生在第 1 层绕组的匝间短路, 信息维数从 0.967 1 下降为 0.952 4, 下降幅度较小 。对于第 2 层绕匝间短路, 特征曲线的信息维数几乎保持不变 。第 3 层匝间短路的 特征曲线信息维数下降速率加快, 但在第 21 匝短路时出 现突增 。第 4 层匝间短路的特征曲线信息维数变化幅度 同样较小 。信息维数刻画的是分形对象在空间中分布的疏密程度, 随着短路位置变化, 特征曲线在空间内的分 布逐渐稀疏, 与信息维数的降低趋势相符。
随 着 短 路 位 置 变 化, 关 联 维 数 由 0.964 2 减 少 为 0.559 5, 变化幅度相比盒维数与信息维数更大, 且呈现 “阶梯状”降低的趋势, 即在每一层最后一匝短路和下一 层第 1 匝短路之间产生较大幅度的降低, 而同一层各匝 短路的关联维数值相差较小 。因此, 各层绕组匝间短路 之间的关联维数具有良好的区分度 。关联维数为奇异吸 引子维数的概率测度, 较之信息维数和盒维数, 对动力 学系统吸引子的不均匀性反映更敏感, 从而更好地提供 系统维数和复杂性的信息[21] 。关联维数的降低对应波形 的复杂程度和不规则程度降低 。当关联维数为 1 或 2 时, 表明系统表现出周期或拟周期运动, 除此之外, 则说明 系统为对初始条件敏感的混沌运动 。根据第 3. 1 节的分 析, 反射波特征曲线对匝间短路发生的位置高度敏感, 与关联维数计算结果相符合。
4 基于 BP 神经网络的绝缘故障评估
人工神经网络是一种得到广泛应用的“黑箱”模型, 通过对样本进行训练学习, 可以建立复杂的高维度非线性 映射关系, 具有良好的泛化能力, 而神经网络内部对外 呈现“黑箱”状态。使用人工神经网络作为评估分合闸线 圈绝缘故障的工具, 选取反射波特征曲线的盒维数、信息 维数与关联维数作为特征参数, 挖掘特征参数与故障位置 之间的内在映射关系, 从而构建故障位置评估模型[21-23]。
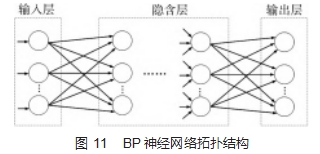
BP (Back Propagation) 神经网络是一种依据误差逆 向传播进行训练学习的多层前馈网络, 是应用最广泛的 人工神经网络之一, 其拓扑结构如图 11 所示[ 19-20] 。BP 神 经网络依次计算输出层 、隐含层 、输入层的误差, 然后根据误差与各层神经元权值和阈值的数学关系不断调整 权值与阈值, 使 BP 神经网络的误差逐渐降低, 从而提高 网络的精度。
对于该分合闸线圈波阻抗模型, 将 21 层绕组从首端 到末端分为 4 段, 第 1 层绕组到第 5 层绕组定义为第 1 段, 第 6 层绕组到第 10 层绕组定义为第 2 段, 第 11 层绕组到 第 15 层绕组定义为第 3 段, 第 16 层到第 21 层绕组定义为 第 4 段 。采用 BP 神经网络对绕组匝间短路故障位置进行 评估 。输入参数为特征曲线的盒维数 、信息维数与关联 维数, 输出为匝间短路故障位置, 绕组第 1 、2 、3 、4 段 发生的匝间短路故障依次编码为 1 、2 、3 、4。
隐含层神经元的个数直接关系到网络的性能 。当个 数过少时, 网络学习能力较差, 不能形成复杂的映射关 系; 个数过多时, 会导致训练时间长, 对训练样本过拟 合等 。本文参考如式 ( 9 ) 所示的隐含层神经元最佳个数 经验公式, 选择神经元个数为 5。
式中: n 为隐含层神经元个数; l 为输入层神经元个数; m 为输出层神经元个数; a 为 1~ 10 之间的常数。
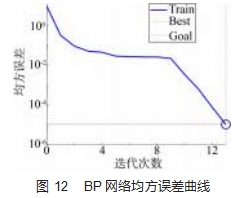
由 ATP-EMTP 仿真获得 80 组包含输入参数和短路位 置的样本数据, 从其 4 个故障位置中各随机抽取 2 组, 共 8 组样本数据作为测试集, 用来在网络训练完成后验证 网络的评估准确率, 剩下 72 组数据作为训练模型的训练 集 。训练最大迭代次数设置为 1 000 次, 目标均方误差设 置为 1 × 10-5, 训练过程中网络均方误差随迭代次数变化 曲线如图 12 所示 。 网络在第 13 次迭代达到目标均方误 差, 网络训练完成。
训练完成后输入训练集的 8 组数据, 进行评估准确 率的验证, 短路故障程度的 BP 神经网络评估结果如表 1 所示, 可见匝间短路故障的位置评估正确率为 100%。
5 结束语
本文提出将行波反射法应用于断路器分合闸线圈匝 间短路故障位置的评估 。通过 ATP-EMTP 软件建立分合 闸绕组的波阻抗模型, 分析了不同短路位置下的反射波 特征曲线, 结论如下:
( 1 ) 不同匝间短路位置的反射波特征曲线呈现出非 线性 、非平稳的特点 。 由于每匝线圈波阻抗不同, 反射 波回到首端的过程中会发生多次折反射, 因此短路位置 对特征曲线的影响十分复杂。
( 2 ) 随着短路位置向绕组末端移动, 盒维数未呈现 明显的变化规律, 关联维数与信息维数逐渐下降, 其中 关联维数下降幅度更大 。关联维数能够较好地区分各层 绕组匝间短路, 对于同一层绕组内的匝间短路, 关联 维数值相差较小; 不同层绕组之间的关联维数数值相 差较大。
( 3 ) 将短路位置划分为 4 段, 基于 BP 神经网络建立 输入参数为盒维数 、信息维数与关联维数, 输出参数为 匝间短路位置的分合闸线圈匝间短路位置评估模型, 测 试集评估准确率为 100%, 表明该方法具有可行性。
参考文献:
[1] 徐国政, 张节容, 钱家骊, 等 . 高压断路器原理和应用[M]. 北 京:清华大学出版社, 2000.
[2] 张大波, 何怡刚 . 基于状态监测与变电站风险的断路器预防 性维修决策[J]. 电力科学与技术学报, 2014, 29(3): 13- 19.
[3] 张帅, 彭在兴, 李锐海, 等 . 断路器分合闸线圈电流波形的差 异机制研究[J]. 高压电器, 2020, 56(6): 165- 172.
[4] 彭在兴, 王颂, 刘芹, 等 . 高压断路器分合闸线圈电流采集实 验平台与故障模拟实验研究[J]. 高压电器 , 2018,54(7): 248-253.
[5] 孙银山, 张文涛, 张一茗, 等 . 高压断路器分合闸线圈电流信 号特征提取与故障判别方法研究[J]. 高压电器 , 2015, 51(9):134- 139.
[6] 李东旭,蔡利忠, 莘尚军,等 .220 kV 瓷柱式 SF6 断路器加热保 温装置设计及应用[J]. 内蒙古电力技术,2021,39(2):73-75.
[7] 褚飞航, 黄虎, 彭在兴, 等 . 252 kV 断路器分合闸线圈在环境 因 素 下 的 劣 化 规 律 研 究 [J]. 电 力 自 动 化 设 备 , 2021, 41(2):218-224.
[8] 王贵山, 李应宏 . 断路器分合闸线圈的绝缘缺陷与改进措施分析[J]. 高压电器, 2016, 52(9): 196- 199.
[9] 王昭雷, 赵士建 . 断路器控制线圈匝间绝缘故障检测仪的研 发及应用[J]. 电工技术, 2020(2): 116- 117.
[ 10] 何军娜, 陈剑云, 艾颖梅, 等 . 电力系统行波测距方法及其发 展[J]. 电力系统保护与控制, 2014,42(24): 148- 154.
[ 11] CHEN Y, DONG L, XU B Y. Wide-area traveling wave fault lo ⁃ cation system based on IEC61850[J].IEEE Trans on Smart Grid, 2013, 4(2): 1207- 1214.
[ 12] 位韶康, 陈平, 姜映辉 . 一种不受波速影响的单端行波测距 方法[J]. 电力系统保护与控制, 2013( 13): 76-81.
[ 13] 贾志东, 陈海, 张征平, 等 . 采用重复脉冲法诊断发电机转子 绕组匝间短路故障[J]. 高电压技术, 2012, 38( 11): 2927-2933.
[ 14] 李卓昕, 彭敏放, 黄清秀, 等 . 行波反射法在变压器绕组匝间 短路故障定位中的应用[J]. 电力系统保护与控制 , 2016, 44 (21): 84-89.
[ 15] 唐治平, 彭敏放, 李光明, 等 . 基于重复脉冲法的变压器绕组匝 间短路故障诊断[J]. 电力自动化设备, 2018, 38( 10): 153- 158.
[ 16] 徐偲畅 . 基于场路结合的 35kV 变电站雷电侵入波分析[D]. 北京:华北电力大学(北京), 2017.
[ 17] 刘伟强 . 分形理论在故障诊断中的应用研究[D]. 长沙 : 国防 科技大学, 2018.
[ 18] 王强, 王莉, 沈进锐 . 基于多重分形与 SVM 的异步电动机轴 承故障诊断[J]. 测控技术, 2017,36( 11): 18-22.
[ 19] 姚杨, 林金涛, 刘洪正, 等 . 基于复合特征的断路器机械故障 诊 断 方 法 研 究 [J]. 中 国 电 机 工 程 学 报 , 2019, 39(21): 6439-6452.
[20] ZHANG Y, REN G, WU D, et al. Rolling bearing fault diagno⁃ sis utilizing variational mode decomposition based fractal di ⁃ mension estimation method[J]. Measurement, 2021, 181( 1/2):109614.
[21] 王宁,马峥嵘, 贾清泉,等 . 基于相空间重构的电压缺口检测及 特征参数辨识[J]. 中国电机工程学报,2017,37( 18):5220-5227.
[22] 熊一, 詹智红, 柯方超, 等 . 基于改进 BP 神经网络的变电站检 修运维成本预测[J]. 电力科学与技术学报 , 2021, 36(4): 44-52.
[23] 袁佳波, 徐鹏程, 李磊, 等 . 基于鸡群优化 BP 神经网络的变 压器油纸绝缘老化预测方法[J]. 电力科学与技术学报, 2020, 35(4): 33-41.
[24] LIU X, MA M, GUO W, et al. Inverter Fault diagnosis based on optimized BP neural network[C]//Proceedings of 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA).New York:IEEE, 2021.
关注SCI论文创作发表,寻求SCI论文修改润色、SCI论文代发表等服务支撑,请锁定SCI论文网!
文章出自SCI论文网转载请注明出处:https://www.lunwensci.com/ligonglunwen/63868.html




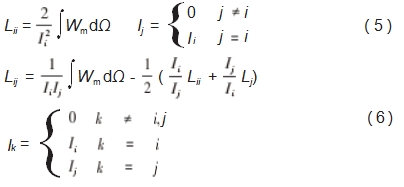






 为落入所有盒子的点数。
为落入所有盒子的点数。